Название: Линейные электрические цепи

Вид работы: курсовая работа

Рубрика: Физика

Размер файла: 61.69 Kb

Скачать файл: referat.me-340972.docx

Краткое описание работы: Решение задач: линейные электрические цепи постоянного и синусоидального тока и трехфазные электрические цепи синусоидального тока. Метод контурных токов и узловых потенциалов. Условия задач, схемы электрических цепей, поэтапное решение и проверка.

Линейные электрические цепи

Министерство образования Российской Федерации

Государственное образовательное учреждение

высшего профессионального образования

Череповецкий Государственный Университет

Кафедра Электропривода и электротехники

Курсовая работа

по дисциплине «Электротехника и электроника»

Выполнил студент

группы 5 ЭН – 22

Малинин М.С.

Проверил доцент

Кудрявцева А.К.

г. Череповец

2007 г

СОДЕРЖАНИЕ

ВВЕДЕНИЕ. 3

ОСНОВНАЯ ЧАСТЬ. 6

ЗАДАЧА 1. 6

Метод контурных токов. 7

Метод узловых потенциалов. 9

ЗАДАЧА 2. 11

ЗАДАЧА 3. 13

ЗАДАЧА 4. 15

СПИСОК ЛИТЕРАТУРЫ.. 17

ВВЕДЕНИЕ

Полупроводниковый диод, двухэлектродный электронный прибор на основе полупроводникового (ПП) кристалла. Понятие «Полупроводниковый диод» объединяет различные приборы с разными принципами действия, имеющие разнообразное назначение.

В полупроводниковых диодах используется свойство p-n перехода, а также других электрических переходов, а также других электрических переходов хорошо проводить электрический ток в одном направлении и плохо – в противоположном. Эти токи и соответствующие им напряжения между выводами диода называются прямым и обратным токами, прямым и обратным напряжениями.

По способу изготовления различают сплавные диоды, диоды с диффузионной базой и точечные диоды. В диодах двух первых типов переход получается методами сплавления пластин p- и n-типов или диффузии в исходную полупроводниковую пластину примесных атомов. При этом p-n-переход создается на значительной площади (до 1000 мм2). В точечных диодах площадь перехода меньше 0,1 мм2. они применяются главным образом в аппаратуре сверхвысоких частот при значении прямого тока 10 – 20 мА.

По функциональному назначению полупроводниковые диоды делятся на выпрямительные, импульсные, стабилитроны, фотодиоды, светоизлучающие диоды и т.д.

Выпрямительные диоды предназначены для преобразования переменного тока и выполняются по сплавной или диффузионной технологии. Прямой ток диода направлен от анодного А к катодному К выводу. Нагрузочную способность выпрямительного диода определяют: допустимый прямой ток Iпр и соответствующее ему прямое напряжение Uпр, допустимое обратное напряжение Uобр и соответствующий ему обратный ток Iобр, допустимая мощность рассеяния Pрас и допустимая температура окружающей среды (до 50 0С для германиевых и до 140 0С для кремниевых диодов).

Вследствие большой площади p-n-перехода допустимая мощность рассеяния выпрямительных диодов малой мощности с естественным охлаждением достигает 1 Вт при значениях прямого тока до 1 А. Такие диоды часто применяются в цепях автоматики и в приборостроении. У выпрямительных диодов большой мощности с радиаторами и искусственным охлаждением (воздушным или водяным) допустимая мощность рассеяния достигает 10 кВт при значениях допустимых прямого тока до 1000 А и обратного напряжения до 1500 В.

Импульсные диоды предназначены для работы в цепях формирования импульсов напряжения и тока.

Стабилитроны, называемые также опорными диодами, предназначены для стабилизации напряжения. В этих диодах используется явление неразрушающего электрического пробоя (лавинного пробоя) p-n-перехода при определенных значениях обратного напряжения Uобр = Uпроб.

Следует отметить основные причины отличия характеристик реальных диодов от идеализированных. Обратимся к прямой ветви вольт-амперной характеристики диода (u > 0, ί > 0). Она отличается от идеализированной из-за того, что в реальном случае на нее влияют:

· сопротивления слоев полупроводника (особенно базы);

· сопротивления контактов металл-полупроводник.

Важно, что сопротивление базы может существенно зависеть от уровня инжекции (уровень инжекции показывает, как соотносится концентрация инжектированных неосновных носителей в базе на границе перехода с концентрацией основных носителей в базе). Влияние указанных сопротивлений приводит к тому, что напряжение на реальном диоде при заданном токе несколько больше (обычно на доли вольта).

Обратимся к обратной ветви (u < 0, ί < 0). Основные причины того, что реально обратный ток обычно на несколько порядков больше теплового тока ίs, следующие:

· термогенерация носителей непосредственно в области p-n-перехода;

· поверхностные утечки.

Термогенерация в области p-n-перехода оказывает существенное влияние на ток потому, что область перехода обеднена подвижными носителями заряда, и процесс рекомбинации (обратный процессу генерации и в определенном смысле уравновешивающий его) здесь замедлен.

ОСНОВНАЯ ЧАСТЬ

ЗАДАЧА 1 Линейные электрические цепи постоянного тока

Для электрической схемы выполнить следующее:

· Упростить схему, заменив последовательно и параллельно соединенные резисторы четвертой и шестой ветвей эквивалентными, а источники тока преобразовать в источники напряжения. Дальнейший расчет вести для упрощенной схемы.

· Указать на схеме положительное направление токов в ветвях и обозначить эти токи.

· Определить токи во всех ветвях схемы методом контурных токов.

· Определить токи во всех ветвях схемы методом узловых потенциалов.

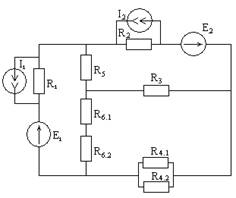
Метод контурных токов

Дано:

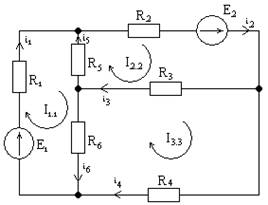R1 = 19,5 Ом E1 = 25,8 В

R2 = 60 Ом E2 = 37,5 В

R3 = 90 Ом E3 = 0 В

R4.1 = 150 Ом I1 = 0,04 А

R4.2 = 600 Ом I2 = 0 А

R5 = 165 Ом I3 = 0 А

R6.1 = 40 Ом R6.2 = 27,5 Ом

Решение:

1. Находим в схеме элементы, соединенные параллельно или последовательно, и заменяем их эквивалентными

R4 = R4.1· R4.2 / (R4.1 + R4.2 ) = 150 · 600 / (150 + 600) = 120 Ом

R6 = R6.1 + R6.2 = 40 + 27,5 = 67,5 Ом

2. Определяем ЭДС

E1’= I1 · R1 =0,04 · 19,5 = 0,78 В

E2’= I2· R2 = 0 · 60 = 0 В

E1*= E1–E1’= 25,8 – 0,78 = 25,02 В

E2*= E2’– E2= 37,5 – 0 = 37,5 В

3. Составляем систему уравнений

I1.1 · (R1 + R5 + R6) – I2.2 · R5 – I3.3 · R6 = E1

I1.1 · R5 + I2.2 · (R2 + R3 + R5) – I3.3 · R3 = – E2

6 – I2.2 · R3 + I3.3 · (R3 + R4 + R6) = 0

Переписываем систему уравнений с числовыми коэффициентами

I1.1 · (19,5 + 165 + 67,5) – I2.2 · 165– I3.3 · 67,5 = 25,02

– I1.1 · 165+ I2.2 · (60 + 90 + 165) – I3.3 · 90= 37,5

I1.1 · 67,5– I2.2 · 90+ I3.3 · (90 + 120+ 67,5) = 0

252 I1.1 – 165 I2.2 – 67,5 I3.3 = 25,02

– 165 I1.1 + 315 I2.2 – 90 I3.3 = 37,5

– 67,5 I1.1 – 90 I2.2 + 277,5 I3.3 = 0

4. Считаем определители системы

252 – 165 – 67,5

Δ = – 165 315 – 90 = 22 027 950 – 1 002 375 – 1 002 375 –

– 67,5 – 90 277,5

– 1 435 218,75 – 2 041 200 – 7 554 937,5 = 8 991 843,75

25,02 – 165 – 67,5

Δ1 = 37,5 315 – 90 = 2 187 060,75 + 2 278 812,5 +

0 – 90 277,5

+ 797 343,75 – 202 662 + 1 717 031,25 = 4 726 586,25

252 25,02 – 67,5

Δ2 = – 165 37,5 – 90 = 2 622 375 + 151 996,5 –

– 67,5 0 277,5

– 170 859,375 + 1 145 603,25 = 3 749 115,375

252 – 165 25,02

Δ3 = – 165 315 37,5 = 371 547 + 417 656,25 + 531 987,75 +

– 67,5 – 90 0

+ 850 500 = 2 171 691

5. Определяем контурные токи

I1.1 = Δ1 / Δ = 0,526

I2.2 = Δ2 / Δ = 0,417

I3.3 = Δ3 / Δ = 0,242

6. Используя II закон Кирхгофа, определяем токи в цепях

ί1 = I1.1 = 0,526 А ί4 = I3.3 = 0,242 А

ί2 = I2.2 = 0,417 А ί5 = I2.2 – I1.1 = – 0,109 А

ί3 = I2.2 – I3.3 = 0,175 А ί6 = I1.1 – I3.3 = 0,284 А

7. Проверка

ί5 + ί1 – ί2 = – 0,109 + 0,526 – 0,417 = 0

ί3 – ί6 – ί5 = 0,175 – 0,284 + 0,109 = 0

ί6 + ί4 – ί1 = 0,284 + 0,242 – 0,526 = 0

ί2 – ί3 – ί4 = 0,417 – 0,175 – 0,242 = 0

Метод узловых потенциалов

Дано:

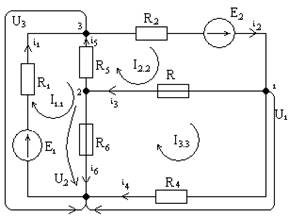R1 = 19,5 Ом E1 = 25,8 В

R2 = 60 Ом E2 = 37,5 В

R3 = 90 Ом E3 = 0 В

R4.1 = 150 Ом I1 = 0,04 А

R4.2 = 600 Ом I2 = 0 А

R5 = 165 Ом I3 = 0 А

R6.1 = 40 Ом R6.2 = 27,5 Ом

Решение:

1. Определяем собственную проводимость узла, которая равна сумме проводимостей, сходящихся в узле

g1 = 1 / R1 = 0,05 g4 = 1 / R4 = 0,01

g2 = 1 / R2 = 0,02 g5 = 1 / R5 = 0,01

g3 = 1 / R3 = 0,01 g6 = 1 / R6 = 0,01

2. Определяем взаимную проводимость в узле, которая равна проводимости ветви, соединяющей два узла

g1.1 = g4 + g2 + g3 = 0,04 g1.2 = g2.1 = g3 = 0,01

g2.2 = g3 + g5 + g6 = 0,03 g2.3 = g3.2 = g5 = 0,01

g3.3 = g1 + g2 + g5 = 0,08 g1.3 = g3.1 = g2 = 0,02

3. Определяем сумму токов от источников, которые находятся в ветвях, сходящихся в данном узле

I1.1 = – E2 / R2 = – 37,5 / 60 = – 0,625

I2.2 = 0

I3.3 = E1 / R1+ E2 / R2 = 25,02 / 19,5 + 37,5 / 60 = 1,905

4. Записываем в общем виде систему уравнений

u1 · g1.1 – u2 · g1.2 – u3 · g1.3 = I1.1

– u1 · g2.1 + u2 · g2.2 – u3 · g2.3 = I2.2

– u1 · g3.1 – u2 · g3.2 + u3 · g3.3 = I3.3

5. Переписываем систему уравнений с числовыми коэффициентами

0,04 u1 – 0,01 u2 – 0,02 u3 = – 0,63

– 0,01 u1 + 0,03 u2 – 0,01 u3 = 0

– 0,02 u1 – 0,01 u2 + 0,08 u3 = 1,91

6. Считаем определители системы

0,04 – 0,01 – 0,02

Δ = – 0,01 0,03 – 0,01 = 0,000096 – 0,000002 – 0,000002 –

– 0,02 – 0,01 0,08

– 0,000012 – 0,000004 – 0,000008 = 0,000068

– 0,63 – 0,01 – 0,02

Δ1 = 0 0,03 – 0,01 = – 0,001512 + 0,000191 + 0,001146 +

1,91 – 0,01 0,08

+ 0,000063 = – 0,000112

0,04 – 0,63 – 0,02

Δ2 = – 0,01 0 – 0,01 = – 0,000126 + 0,000382 + 0,000764 –

– 0,02 1,91 0,08

– 0,000504 = 0,000516

0,04 – 0,01 – 0,63

Δ3 = 0,01 0,03 0 = 0,002292 – 0,000063 – 0,000378 –

– 0,02 – 0,01 1,91

– 0,000191 = 0,00166

7. Определяем узловые напряжения

U1.1 = Δ1 / Δ = – 1,647 В

U2.2 = Δ2 / Δ = 7,588 В

U3.3 = Δ3 / Δ = 24,412 В

8. Используя II закон Кирхгофа, определяем токи в ветвях

ί1 = (E1 – U3) / R1 = (25,02 – 24,412) / 19,5 = 0,03 А

ί2 = (– E2 – U1 + U3) / R2 = (– 37,5 + 1,647 + 24,412) / 60 = – 0,19 А

ί3 = (U1 – U2) / R3 = (– 1,647 – 7,588) / 90 = – 0,1 А

ί4 = U1 / R4 = – 1,647 / 120 = – 0,01 А

ί5 = (– U3 + U2) / R5 = (– 24,412 + 7,588) / 165 = – 0,1 А

ί6 = U2/ R6 = 7,588 / 67,5 = 0,11 А

9. Проверка

ί5 + ί1 – ί2 = – 0,1 + 0,03+ 0,191 = 0,12

ί3 – ί6 – ί5 = – 0,1 – 0,11 + 0,11 = – 0,11

ί6 + ί4 – ί1 = 0,11 – 0,01 – 0,03 = 0,07

ί2 – ί3 – ί4 = – 0,19+ 0,1 + 0,01 = – 0,08

ЗАДАЧА 2Линейные электрические цепи синусоидального тока

В сеть переменного тока с действующим значением напряжения U включена цепь, состоящая из двух параллельных ветвей. Определить показания приборов, реактивную мощность цепи, коэффициент мощности и построить векторную диаграмму напряжений. Указать на схеме положительное направление токов в ветвях и обозначить эти токи.

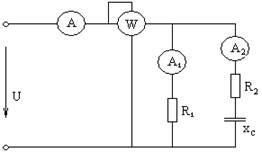
Дано:

R1 = 8 Ом

R2 = 2 Ом

U = 127 В

јxc = 17 Ом

Решение:

1. Примем начальную фазу напряжения равной нулю

Ů = 127 е ј0 В

2. Определяем комплексное сопротивление

z 1 = R1 = 8 Ом

z2 = R2 – јxc = √2 2 + 17 2 · е – ј arctg 17/4 = 17,1 е – 77

3. По закону Ома определяем комплексные точки

İ 1 = Ů / z1 = 127 е ј0 / 8 = 15,9 е ј0 А

İ 2 = Ů / z2 = 127 е ј0 / 17,1 е – 77 = 7,4 е ј 77 =

= 7,4 · cos 77 + ј 7,4 · sin 77 = 1,7 + ј 7,2

4. Определяем полный комплексный ток

İ = İ 1 + İ 2 = 15,9 е ј0 + 7,4 е ј 77 = 15,9 cos 0 + ј 15,9 sin 0 +

+ 7,4 cos 77 + ј 7,4 sin 77 = 17,5 + ј 7,2 =

= √17,5 2 + 7,2 2 · е ј arctg 7,23/17,544 = 18,9 · е ј 22

А 18,9 А

А1 15,9 А

А2 7,4 А

5. Определяем полную мощность

S = İ · Ů = 18,9 е ј 22 · 127 е ј0 = 2410,5 е ј 22 =

= 2410,5 cos 22 + ј 2410,5 sin 22 = 2234,9 + ј 902,9

İ = 18,9 · еј 22 S = 2410,5 ВА

P = 2234,9 Вт Q = 902,9 ВАР

6. Определяем коэффициент мощности

cos φ = P / S = 0,93

ЗАДАЧА 3 Линейные электрические цепи синусоидального тока

В цепь переменного тока с мгновенным значением напряжения

U = Umsin ωt промышленной частоты f = 50 Гц включены резистор и конденсатор. Определить показания приборов, реактивную и полную мощность цепи. Построить треугольник напряжений и векторную диаграмму напряжений.

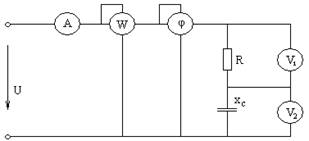
Дано:

R = 2 Ом

Um = 282 В

xc = 17 Ом

Решение:

1. Определяем напряжение на зажимах цепи

U = Um/ √2 = 282 / 1,41 = 200 В

2. Определяем накопленное емкостное сопротивление

– јxc = – ј 17 = 17 е – ј 90

3. Определяем полное комплексное сопротивление цепи z

Z = R – јxc = 2 – ј 17 = √2 2 + 17 2 · е – ј arctg 17/2 = 17,1 е – ј 83

4. Начальную фазу напряжения примем равной нулю

Ů = 200е ј0 В

5. Определяем комплексный ток по закону Ома

İ = Ů / Z = 200 е ј0 / 17,1 е – ј 83 = 11,7 е ј 83

тогда показания амперметра IА = 11,7 А

6. Определяем комплексное напряжение на R

ŮR = I R = 11,7 еј 83 · 2 = 23,4 еј 83 =

= 23,4 cos 83 + ј 23,4 sin 83= 2,9 + ј23,2

7. Определяем напряжение на емкости

Ůc = İ (– ј xc) = 11,7 е ј 83 · 17 е – ј 90 = 198,6 е – ј 7 =

= 198,6 cos 7 – ј 198,6 sin 7 = 197,1 – ј 24,2

тогда показания вольтметра Uc = 198,6 В

8. Определяем полную комплексную мощность цепи

Ŝ = I* · Ů = 11,7 е -ј 83 · 200 е ј0 = 2336 е -ј 83 =

= 2336 cos 83 – ј 2336 sin 83 = 284,7 – ј 2318,6

S = 2336 ВА

P = 284,7Вт Q = 2318,6 ВАР

9. Определяем показатель фазометра

φ = φu – φί = 0 – 83 = – 83

тогда показания фазометра cos φ = cos (– 83) = 0,12

ЗАДАЧА 4Трехфазные электрические цепи синусоидального тока

В трехфазную сеть с линейным напряжением Uл (действующее значение напряжения) по схеме «треугольник/треугольник» включены активно-индуктивные приемники. Определить фазные и линейные токи в нагрузке, активную мощность всей цепи и каждой фазы отдельно.

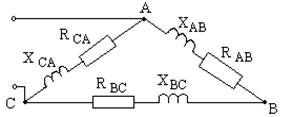
Дано:

RАВ = 8 Ом Uл = 127 В XСА = 3 Ом RСА = 2 Ом

RВС = 3 Ом XАВ = 6 Ом XВC= 17 Ом

Решение:

1. Т. к. рассматриваем соединение «треугольник/треугольник», то

Uп = Uдо

ŮАВ = 127 е ј 0

ŮВС = 127 е – ј 120

ŮСА = 127 е ј 120

2. Определяем комплексное полное сопротивление фаз

zАВ = RАВ + ј xАВ = 8 + ј 6 = √82 + 62 · е ј arctg 6/8 = 10 е ј37

zВC = RВC + ј xВC= 3 + ј 17 = √32 + 172 · е ј arctg 17/3 = 17,3 е ј80

zCА = RСА + ј xСА = 2 + ј 3 = √22 + 32 · е ј arctg 3/2 = 3,6 е ј56

3. Определяем комплексные фазные токи

Iф = Uф / zф

İАВ = 127 е ј 0 / 10 е ј37 = 12,7 е -ј37

İВС = 127 е -ј 120 / 17,3 е ј80 = 7,3 е -ј200

İСА = 127 е ј 120 / 3,6 е ј56 = 35,3 е ј64

4. Определим сопряженные комплексные токи фаз:

İАВ* = 12,7 е ј37

İВС* = 7,3 е ј200

İСА* =35,3е -ј64

5. Определяем комплексные полные мощности фаз

S = IФ* · UФ

SАВ = 12,7 е ј37 · 127 е ј 0 = 1612,9 е ј37 = 1612,9 cos 37 + ј 1612,9 sin 37 = 1288,1 + ј 970,7

SВC = 7,3 е ј200 · 127 е – ј 120 = 927,1 е -ј80 =

= 927,1 cos 80 – ј 927,1 sin80 = 161 – ј 913

SCА = 35,3 е -ј64 · 127 е ј 120 = 4483,1 е ј56 = 4483,1 cos56 + ј 4483,1 sin56 =

= 2506,9 + ј 3716,7

6. Определяем активную мощность фаз

PАВ = 1288,1 Вт

PВC = 161 Вт

PCА = 2506,9 Вт

7. Определяем активную мощность цепи

Pц = PАВ + PВC + PCА = 3956 Вт

СПИСОК ЛИТЕРАТУРЫ

1. Касаткин А. С., М. В. Немцов «Электротехника»: М., Академия, 2005.

2. Методические указания к выполнению контрольной работы по дисциплине «Общая электротехника и электроника» для студентов заочной формы обучения.

3. Лачин В.И., Н.С. Савёлов «Электроника»: М., Феникс, 2002.

4. Лекции по дисциплине «Общая электротехника и электроника».