Название: Методы расчета цепей постоянного тока

Вид работы: контрольная работа

Рубрика: Физика

Размер файла: 59.71 Kb

Скачать файл: referat.me-342982.docx

Краткое описание работы: Разветвленная цепь с одним источником электроэнергии. Определение количества уравнений, необходимое и достаточное для определения токов во всех ветвях схемы по законам Кирхгофа. Метод контурных токов. Символический расчет цепи синусоидального тока.

Методы расчета цепей постоянного тока

Содержание

ЗАДАНИЕ 1. 3

МЕТОДЫ РАСЧЕТА ЦЕПЕЙ ПОСТОЯННОГО ТОКА.. 3

Задача 1. 3

Задача 2. 4

Задача 3b. 5

ЗАДАНИЕ 3. 7

СИМВОЛИЧЕСКИЙ РАСЧЕТ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА 7

Задача 1. 7

ЗАДАНИЕ 1

МЕТОДЫ РАСЧЕТА ЦЕПЕЙ ПОСТОЯННОГО ТОКА

Задача 1

Расчет разветвленной цепи с одним источником электроэнергии. По данным табл.1, 2,3 определить ток в неразветвленной части цепи и ветви, указанной в таблице 1

Дано: ветви, сопротивления

которых равны ¥

(разрыв цепи) – 10,13,15,17

Ветви, сопротивления

которых равны нулю

(к.з. ветви) – 5,6,12

Ветвь, в которой

следует определить ток – 8

U=220 В, r=6,8 Ом

Решение

Для определения тока в неразветвленной части цепи воспользуемся методом эквивалентных преобразований, «сворачивая» схему.

1)

2) Ом

3) 6,8 Ом

4) 5,83 Ом

5) Ом

6) Ом

В результате всех преобразований получили схему:

По закону Ома:

32,64 А

Далее находим ток в указанной ветви – ветви 8.

Для этого разворачиваем схему:

Согласно схеме ток в ветви № 8 равен:

Задача 2

По данным табл. 4 определить количество уравнений, необходимое и достаточное для определения токов во всех ветвях схемы по законам Кирхгофа. Составить эти уравнения в общем виде.

Дано: Цепь не содержит ветвей 2,3,5,8

Решение

Количество уравнений, необходимое и достаточное для определения токов в ветвях должно равняться количеству ветвей схемы.

Для данного случая число уравнений равно 4.

Для узла «а»:

Для узла «b»:

Для контура I:

Для контура II:

Составляем систему уравнений:

Задача 3 b

Пользуясь методом контурных токов, определить значения и направления всех токов в ветвях схемы по данным табл. 5,6,7. Составить численный баланс мощностей.

Дано: Цепь не содержит ветвей 2,3,5,8

R₁ = 18Ом, R₄ = 28Ом,R₆ = 20Ом,

R₇ = 38Ом, R₉ = 20Ом, R₁₀ = 60Ом,

Е₁ = 70В, Е₂ = 50В,Е₃ = 30В,Е₄ = 70В,

Е₅ = 120В, Е₆ = 60В, Е₇ = 80В, Е₈ = 90В,

Е₉ = 130В, Е₁₀ = 45В, U₂ = 200В

Решение

Составляем уравнения для трех контуров:

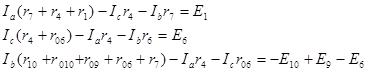
Подставляем числовые значения сопротивлений и э.д.с.

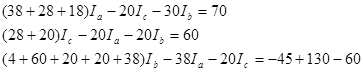
После упрощения получили:

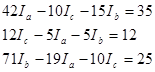
Решив полученную систему уравнений, получили:

=-0,013841А, =-0,183391А, =-2,249827 А.

Задаемся произвольными положительными направлениями токов, действующих в ветвях, и определяем их как алгебраическую сумму контурных токов. При этом если направление контурного тока и тока, действующего в ветви, совпадают, то при суммировании такой контурный ток следует брать со знаком «плюс», в противном случае – со знаком «минус». Если в ветви протекает только один контурный ток, то действующий в ветви ток будет равен контурному:

Составляем баланс мощности

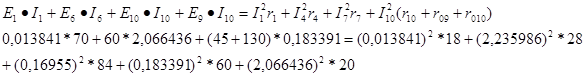227,0485=229,3138

ЗАДАНИЕ 3

СИМВОЛИЧЕСКИЙ РАСЧЕТ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА

Задача 1

По данным табл. 9,10,11 рассчитать токи в ветвях заданной цепи при f = 50 Гц. Используя данные расчета, записать мгновенное значение указанной в табл. 9 величины. Составить баланс мощностей. В масштабе построить топографическую диаграмму.

Дано: Цепь не содержит элементов L₂ , C₁ .

U=100B, Y_u = 70⁰ ,

r₁ = 10Ом, r₂ = 10Ом,R₃ = 5,6Ом,

L₁ = 8,7 мГн, L₃ = 47,8 мГн,

C₂ =120мкФ, C₃ =318 мкФ

Решение

1.Определяем реактивные сопротивления ветвей:

2. Определяем полные сопротивления ветвей:

Определяем комплексное сопротивление всей цепи:

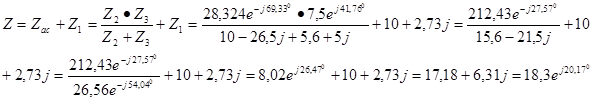
Записываем приложенное напряжение в комплексной форме и определяем ток I₁ в неразветвленной части цепи:

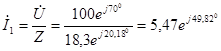А

Определяем напряжение на разветвленном участке цепи «ас»

Определяем токи в остальных ветвях:

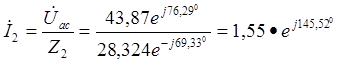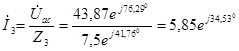А

А

Записываем мгновенное значение напряжения и_{L 1} по его комплексному действующему значению

В

Комплексная амплитуда напряжения

В

и_{L 1} =

Комплексную мощность всей цепи определяем как

В*А

По закону сохранения энергии активная мощность всей цепи равна сумме активных мощностей всех n активных сопротивлений, входящих в цепь:

Вт

По закону сохранения энергии реактивная мощность всей цепи равна алгебраической сумме мощностей всех m реактивных сопротивлений, входящих в цепь.

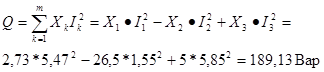
Баланс активных и реактивных мощностей сходится:

Топографическая диаграмма – это векторная диаграмма цепи, в которой каждой точке электрической схемы соответствует точка на топографической диаграмме. Это достигается тем, что векторы напряжений на отдельных элементах схемы строятся в той последовательности, в которой они расположены в схеме (обходим схему в направлении тока).

Для построения топографической диаграммы определяем напряжения на всех элементах цепи.

Выбираем масштабы по току и напряжению:

1В=1мм

1А = 1см.