Название: Расчет поляризационных характеристик оптических резонаторов

Вид работы: реферат

Рубрика: Физика

Размер файла: 180.51 Kb

Скачать файл: referat.me-341623.docx

Краткое описание работы: Санкт-Петербургский Государственный Электротехнический Университет СПбГЭТУ («ЛЭТИ») Пояснительная записка к курсовому проекту по дисциплине «Теоретические основы квантовых приборов»

Расчет поляризационных характеристик оптических резонаторов

Санкт-Петербургский Государственный Электротехнический Университет

СПбГЭТУ («ЛЭТИ»)

Пояснительная записка

к курсовому проекту

по дисциплине «Теоретические основы квантовых приборов»

по теме «Расчет поляризационных характеристик оптических резонаторов»

Вариант № 12

Выполнил: Макаров А.М.

Группа 7585

Проверила: Баринова Е.А.

Санкт-Петербург

2010

Содержание

Введение……………………………………………………………………………………..3

1. Нахождение в общем виде матрицы резонатора……………………………………….5

2. Нахождение собственных значений матриц…………………………………………...6

3. Нахождение отношения компонент собственных векторов, добротности и расщепления частот……………………………………………………………………………...7

Вывод…………………………………………………………………………………….…10

Введение

Проектирование лазерных приборов и систем требует определения поляризационных характеристик оптических резонаторов. Оптические резонаторы обычно содержат различные оптические элементы, изменяющие характер поляризации проходящего через них света. Поляризация светового пучка, генерируемого лазером, определяется конфигурацией оптического резонатора и набором оптических элементов, расположенных в нем. Кроме поляризации генерируемого светового пучка поляризационные характеристики резонатора определяют в значительной степени частоту генерируемого света и его фазовые характеристики, что особенно важно при расчете лазеров с кольцевым резонатором, являющихся основой лазерных гироскопов.

Для расчета поляризационных характеристик обычно используют матричный метод Джонса, основанный на разложении вектора Е электрического поля плоской ЭМВ на две ортогональные компоненты Е_х и Е_у :

,, где – амплитуды 2х ортогональных компонент, – их фазы, – частота ЭМВ.

В методе Джонса электрическое поле волны записывается в виде столбца:

. Множитель несет информацию об абсолютной фазе колебания. Нас интересует изменение фазовых соотношений при прохождении анизотропных элементов между компонентами , поэтому в дальнейшем опускается.

Данное представление достаточно чтобы описать любую поляризацию.

При прохождении плоской ЭМВ через анизотропный элемент изменение поляризации происходит по закону

, или .

Коэффициенты характеризуют свойства анизотропного элемента. Матрица такого элемента в целом М= характеризует изменение амплитуд и фаз компонент ЭМВ при прохождении анизотропного элемента и изменение ее поляризации.

Поляризатор – устройство, преобразующее проходящий через него свет произвольной поляризации в свет заданной поляризации. Линейный поляризатор преобразует свет произвольной поляризации в свет с линейной поляризацией, циркулярный, соответственно, в свет с круговой поляризацией.

Линейный поляризатор разделяет падающий на него пучок света на две взаимно ортогональные линейно-поляризованные компоненты – одну пропускает, другую поглощает. Принцип действия такого поляризатора основан на использовании двойного лучепреломления или дихроизма.

Матрицы идеального поляризатора имеют вид М= и М=.

Дихроичный поляризатор, разделяющий ЭМВ на две линейно поляризованные компоненты с поглощением одной из них, не является идеальным. Матрица линейного дихроичного поляризатора записывается в виде М=, обычно ,

0<.

Линейная фазовая пластинка. Толщина dудовлетворяет условию

, где m– целое число, 0≤а≤1. Тогда две компоненты светового луча, на которые он расщепляется при двулучепреломлении, сдвигаются по фазе одна относительно другой на величину . Матрица линейной фазовой пластинки имеет вид М=.

Одной из важнейших характеристик резонатора является его добротность:

, где - энергия волны, запасенная в резонаторе, а - энергия, теряемая за один проход резонатора. Добротность резонатора пропорциональна его длине и обратно пропорциональна его потерям .

При наличии разности набега фаз в резонаторе возникает расщепление частот для собственных поляризаций

∆n=, так как изменение фазы на соответствует переходу от одной моды к следующей, т.е. ∆, ∆n_м =или ; ∆n=.

Для кольцевого резонатора , ∆n_м =, поэтому∆n=.

Расчет кольцевого резонатора несколько отличается от расчета линейного резонатора, так как для кольцевого резонатора из-за ненулевого угла падения необходимо рассчитывать различие коэффициентов отражения для различных поляризаций R_х ≠ R_у . Для простоты зеркала считают изотропными. Тогда при достаточно большом угле падения выражение матрицы зеркала имеет вид R=

При нечетном числе зеркал суммарная матрица зеркал резонатора имеет вид

R_Ʃ =, при четном числе зеркал анизотропия не проявляется: R_Ʃ =.

1. Нахождение в общем виде матрицы резонатора для света, выходящего из точки А в разных направлениях.

.

.

2. Нахождение собственных значений матриц

2.1. V=1, U=0

Анализ собственных значений показывает, что при потери в системе отсутствуют (амплитудный коэффициент равен единице), добротность резонатора равна бесконечности, анизотропия имеет фазовый характер (выражение комплексное).

2.2. V=0,9, U=0,1

= =

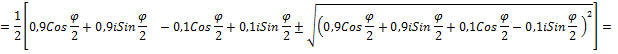
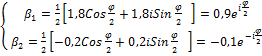
Анализ собственных значений показывает, что при и потери в системе присутствуют, анизотропия имеет амплитудно-фазовый характер (выражение комплексное).

3. Нахождение отношения компонент собственных векторов (собственных поляризаций), добротности резонатора и расщепления частот при различных V, U и

3.1. При V=1, U=0

а) ,

= , собственная поляризация линейная.

Расщепление частот имеет место и равно

n=,

Добротность

= 6.28∞

б) ,

, собственная поляризация линейная.

Расщепление частот имеет место и равно

n=,

Добротность

= 6.28∞

в) ,

, собственная поляризация линейная.

Расщепление частот имеет место и равно

n=,

Добротность

= 6.28∞

3.2. При V=0,9 , U=0,1

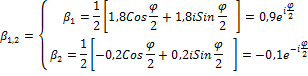
а) , анизотропия амплитудно-фазовая.

= , собственная поляризация линейная

Расщепление частот имеет место и равно

n=,

Добротность

= 6.28

= 6.28

б) , анизотропия амплитудно-фазовая.

, собственная поляризация линейная

Расщепление частот имеет место и равно

n=,

Добротность

= 6.28

= 6.28

в) , анизотропия фазовая.

, собственная поляризация линейная.

Расщепление частот имеет место и равно

n=,

Добротность

= 6.28

= 6.28

Вывод

В ходе выполнения курсовой работы был исследован 3-зеркальный кольцевой резонатор, содержащий линейную фазовую пластинку и частичный поляризатор. Были определены матрицы резонатора для света, выходящего из точки А в разных направлениях. Также были определены собственные поляризации, добротность резонатора и расщепление частот при разных значениях матрицы частичного поляризатора V, U и угла .

Анализ собственных значений показал, что при U=1, V=0, потери в системе отсутствуют (амплитудный коэффициент равен единице), анизотропия имеет фазовый характер (выражение комплексное).

Добротность резонатора обратно пропорциональна его потерям. Следовательно, при , a₁ =1, потери , добротность =∞.