Название: Исследование переходных процессов в электрических цепях с источником постоянного напряжения
Вид работы: лабораторная работа
Рубрика: Физика
Размер файла: 104.47 Kb
Скачать файл: referat.me-341797.docx
Краткое описание работы: Проведение экспериментальных работ при исследовании различных переходных режимов электрических цепей. Работа с электронным осциллографом и получение осциллограммам. Определение постоянной времени и декремента затухания в исследуемых переходных процессах.
Исследование переходных процессов в электрических цепях с источником постоянного напряжения
Министерство науки и образования РФ
Брянский государственный технический университет
Кафедра «Промышленная электроника»
Отчет по теоретическим основам электротехники
Лабораторная работа №8
«Исследование переходных процессов в электрических цепях с источником постоянного напряжения»
Выполнили студенты группы 04 ПЭ
Гайков В.А., Соколов А.А.,
Шкуратов А.А., Саченко Е.А.
Преподаватель Потапов Л.А.
Брянск 2006
Цель работы: получение навыков проведения экспериментальных работ при исследовании различных переходных режимов электрических цепей.
Задачи работы
1. Закрепить навыки работы с электронным осциллографом;
2. Освоить навыки получения осциллограммам в цепях RC, RL, RLC;
3. Научиться опытным путем определять постоянную времени и декремент затухания в исследуемых переходных процессах.
Выполнение работы
Схема для первых двух пунктов представлена на рис.1.
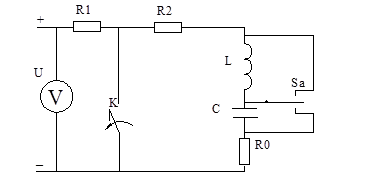
Рис.1
Параметры схемы рис.1
| R1,Oм | R2,Ом | R0,Ом | L,Гн | C,мкФ | U,В |
| 268 | 51 | 7 | 0,0566 | 4 | 10 |
1 . Исследование цепи с конденсатором и активным сопротивлением (процессы разряда и заряда).
Масштабы тока и напряжения на экране осциллографа соответственно равны: 
5 В/ед,
0.5 А/ед. Т.е. Uc=
. I=
.
Отсюда можем рассчитать амплитуду для тока и напряжения на конденсаторе в цепи.
Для заряда конденсатора значение напряжение на конденсаторе имеет вид
.
Возьмем на графике 2 точки, отстоящие друг от друга на некий интервал времени 
:
, 
.
Отсюда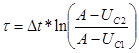 
,
= с.
При разряде конденсатора напряжение имеет вид
,
постоянная времени определяется по формуле
.
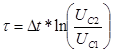Для теоретического расчета параметров переходного процесса составим характеристическое уравнение цепи по методу входного сопротивления:
, 
=
.
Уравнение для тока в цепи
(
).
Полученные результаты занесем в таблицу
Расчетные ( р) и полученные теоретически ( т) параметры переходного процесса в цепи RC
| Режим |  , В |
 , В |
,мс |
р, мс |
т,мс |
| Заряд конденсатора | 2,5 | 6,5 | 2 | 1,5 | 1,3 |
| Разряд конденсатора | 9,5 | 2 | 0,6 | 0,94 | 0,5 |
На осциллографе получаем чередование графиков процессов разряда и заряда конденсатора с частотой (переключения реле – ключ К) 50 Гц.
Построим графики переходного процесса по теоретическим данным.
График напряжения на конденсаторе при его заряде имеет вид
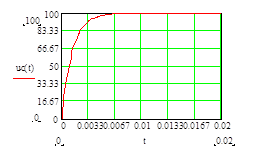
График тока через конденсатор при его заряде
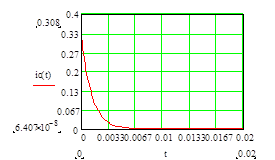
График напряжения на конденсаторе при его разряде
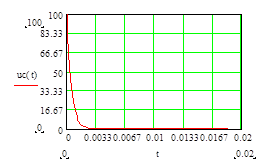
График тока через конденсатор при его разряде
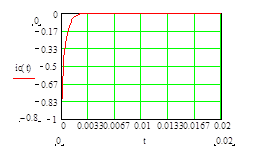
2 . Исследование цепи с катушкой и активным сопротивлением.
Масштабы тока и напряжения на экране осциллографа соответственно равны:
5 В/ед,
0.1 А/ед.
Для подключения катушки значение тока на ней имеет вид
.
Возьмем на графике 2 точки, отстоящие друг от друга на интервал времени :
, 
.
Отсюда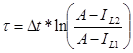 
,
= с.
При отключении катушки 
, постоянная времени определяется по формуле
.
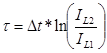Для теоретического расчета параметров переходного процесса составим характеристическое уравнение цепи:
=> 
.
Напряжение на катушке определяется следующей функцией
(
).
Результаты внесем в таблицу
Расчетные ( р) и полученные теоретически ( т) параметры переходного процесса в цепи RL
| Режим |  , A |
 , A |
,мс |
р, мс |
т,мс |
| Подключение катушки | 0,1 | 0,15 | 0,5 | 0,2 | 0,17 |
| Отключение катушки | 0,2 | 0,04 | 0,3 | 0,48 | 0,45 |
На осциллографе получаем чередование графиков процессов отключения и подключения катушки с частотой (переключения реле – ключ К) 50 Гц.
График тока через катушку при ее подключении
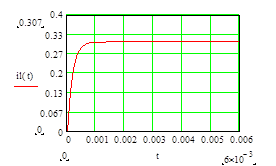
График напряжения на катушке при ее подключении
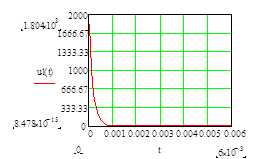
График тока через катушку при ее отключении
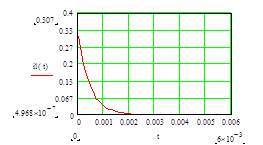
График напряжения на катушке при ее отключении
3 . Исследование цепи с катушкой, конденсатором и активным сопротивлением.
Цепь собрана по схеме, изображенной на рис.2.
Рис.2
Параметры схемы рис.2
| R,Ом | R0,Ом | L,Гн | C,мкФ | U,В |
| 319 | 7 | 0,0566 | 4 | 10 |
В ходе эксперимента мы получили апериодический режим, близкий к критическому (|p1
|>>|p2
|), – при подключении цепи RLC под постоянное напряжение – и затухающий колебательный процесс – при отключении цепи. Напряжение на конденсаторе имеет вид 
- при подключении цепи RLC под напряжение Е – и 
- при отключении цепи. Масштабы тока и напряжения на экране осциллографа соответственно равны: 5 В/ед, 0.2 А/ед.
При подключении цепи RLC постоянная времени определяется по формуле
,
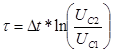а при отключении цепи RLC в качестве параметров переходного процесса выступают декремент затухания и частота свободных колебаний –
, 
, 
.
Для теоретического расчета параметров переходного процесса составим характеристическое уравнение цепи:
1) 
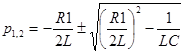- для режима подключения цепи под напряжение (R>
),
2)
; 
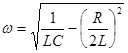- для затухающего колебательного процесса разряда конденсатора на катушку (R<).
Ток и напряжение на катушке описываются следующими функциями:
- при апериодическом режиме
,
;
- при затухающих колебаниях
,
.
Rk=237,9 Ом, активное сопротивление исследуемой цепи при размыкании ключа К R=R+R0=326 Ом.
Поэтому, определяя по осциллограмме апериодического процесса будем считать, что у нас критический режим, и затем сравним результат с полученными из теоретических расчетов 1 и 2 (одно из них будет сравнительно мало). Такое упрощение позволяет с достаточной точностью и простотой оценить результаты.
Расчетные ( р) и полученные теоретически ( т) параметры переходного процесса в цепи RLС
| Режим | , В |
, В |
,мс |
р, мс |
|
 р, с-1
|
т, с-1
|
 р, с-1
|
т, с-1
|
 ,º |
,º |
||||||||
| Апериодический режим | 5 | 8 | 1 | 0,92 | 1,1 | - | - | - | - |
| 0,21 | |||||||||
| Затухающие колебания | 3,5 |
1 |
3 |
- | - |
108,47 | 61,84 | 2094,4 | 2100,75 |
| 87,04 | 88,31 |
На осциллографе получаем чередование графиков процессов отключения и подключения цепи RLC под постоянное напряжение с частотой (переключения реле – ключ К) 50 Гц.
Участки экспериментальных осциллограмм для процессов
А) подключения цепи RLC
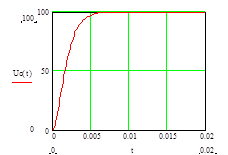
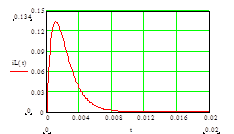
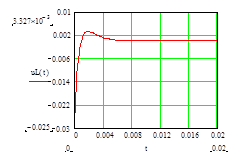
Б) отключения цепи от постоянного напряжения
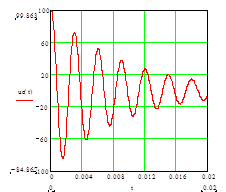
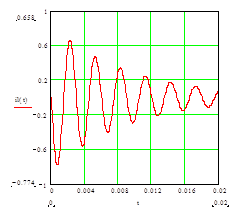
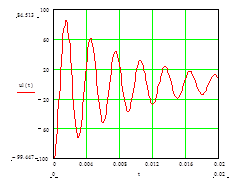
На экране осциллографа наблюдаем протекание процессов в следующей форме
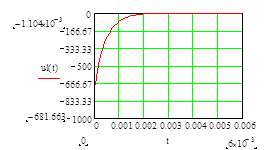
График напряжения на конденсаторе в цепи RLC
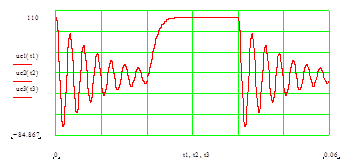
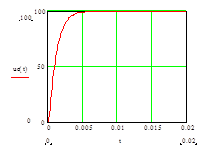
После теоретических расчетов получаем следующие зависимости
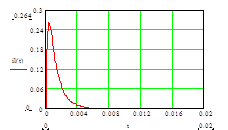
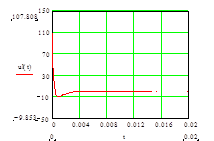
А) подключение цепи RLC под E
(t)=
;
;
.
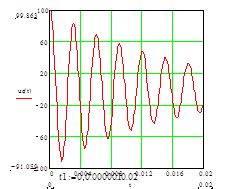
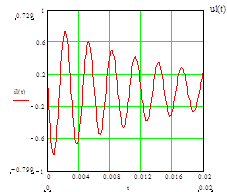
Б) разряд конденсатора на катушку
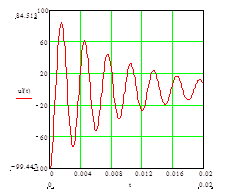
Вывод. При выполнении данной работы мы подробно рассмотрели различные режимы переходных процессов в цепях RC, RL, RLC, подключенных под постоянный ток, и развили навыки определения их параметров с использованием осциллограмм.
Вывод. При проведении эксперимента мы изучили возможности использования электронного осциллографа и применили их к задаче по практическому расчету параметров переходных процессов.
Вывод. Мы ознакомились со всеми режимами переходных процессов в цепях постоянного тока с входным сопротивлением, содержащим вторую степень комплексной частоты, и изучили их особенности.
Вывод. Проведенная работа позволила усвоить методы экспериментального расчета переходных процессов.
Похожие работы
-
Анализ зависимости условного периода логарифмического декремента затухания и добротности контура
Курсовая работа по физике на тему: Анализ зависимости условного периода, логарифмического декремента затухания и добротности контура от его параметров (L,C,R)
-
Расчет переходных процессов в электрических цепях
Контрольная работа по теме: «Расчет переходных процессов в электрических цепях» 1. Рассчитать переходный процесс в электрической цепи I порядка В задании №1 необходимо:
-
Исследование электрических цепей при переходных процессах первого и второго рода
Расчет силы тока и сопротивления по закону Ома. Составление характеристического уравнения и нахождение его корней через вычисление постоянной времени. Собственный магнитный поток и закон его сохранения. Построение графиков функций и схем в мультислим.
-
Расчет переходных процессов в электрических цепях. Формы и спектры сигналов при нелинейных преобразованиях
Расчёт переходных процессов в электрической цепи по заданным схемам: для определения начальных условий; определения характеристического сопротивления; нахождения принужденной составляющей; и временным диаграммам токов и напряжений в электрической цепи.
-
Переходные процессы в колебательных контурах
Колебательные контуры составляют часть аппаратуры связи. Переходные и свободные колебания в параллельном контуре. Режимы переходных колебаний. Переходные колебания в параллельном контуре при гармоническом воздействии. Теория линейных электрических цепей.
-
Исследование биполярного транзистора
Получение входных и выходных характеристик транзистора. Включение биполярного транзистора по схеме с общим эмиттером. Проведение измерения тока базы, напряжения база-эмиттер и тока эмиттера для значений напряжения источника. Расчет коллекторного тока.
-
Анализ переходных процессов в электрических цепях
Характеристика переходных процессов в электрических цепях. Классический и операторный метод расчета. Определение начальных и конечных условий в цепях с ненулевыми начальными условиями. Расчет графиков переходного процесса. Обобщенные характеристики цепи.
-
Экспериментальные исследования электромагнитной индукции 28
Нижегородский Государственный Технический Университет. Лабораторная работа по физике №2-28. Экспериментальные исследования электромагнитной индукции.
-
Расчет переходных процессов в линейных электрических цепях
Расчет токов и напряжения во время переходного процесса, вызванного коммутацией для каждой цепи. Классический и операторный методы. Уравнение по законам Кирхгофа в дифференциальной форме для послекоммутационного режима. Составляющие токов и напряжений.
-
Основные положения теории переходных процессов
Анализ электрической цепи при переходе от одного стационарного состояния к другому. Возникновение переходных колебаний в электрических цепях. Законы коммутации и начальные условия. Классический метод анализа переходных колебаний в электрических цепях.