Пространственная задача о волнообразовании при перемещении импульса давления по поверхности жидк

При движении тела в жидкости со стороны его поверхности к жидкости прилагаются импульсы давлений, создающие вызванные скорости и волнообразование на свободной поверхности.

Качественное представление о картине волнообразования при движении тела можно получить, если исследовать вид волн, возникающих при движении местного импульса давлений П с постоянной скоростью с по поверхности бесконечно глубокой жидкости.

Предположим, что возмущающий центр движется по свободной поверхности жидкости с постоянной скоростью вдоль оси х ; пусть в начальный момент времени этот центр находится в начале координат. При решении задачи воспользуемся методом установившихся фаз.

В произвольной точке Р волнообразование создается за счет наложения концентрических волн, приходящих в эту точку от последовательных точек расположения импульса на оси х . Главная часть этого возмущения возникает от тех концентрических волн, которые приходя в точку Р, имеют одинаковые фазы; волны с различными фазами будут погашать друг друга. Найдем положения Q1 и Q2 импульса на оси х , от которых фазы волн в точке Р постоянны. Для этого необходимо, чтобы при переходе от Q1 к Q2 приращение фазы было равно нулю, т.е.

Тогда, учитывая, что для различных точек Q величины r и t относительно Р переменны, дифференцируя, получим

но согласно рис. 1

тогда

(1)

C помощью этого равенства можно найти положения импульса, которые создают главную часть возмущения в точке Р.

Положим, что одна из этих точек Q1 нами указана на рис.1; отложим ОМ1=, тогда в силу равенства (1) равен 90°. Проведем М1СQ1Р и построим окружность на СР как диаметре; для нее =90°. Следовательно, проводя из Р линию РQ2CМ2, получим точку Q2, для которой тоже справедливо равенство (1), ибо =90°.

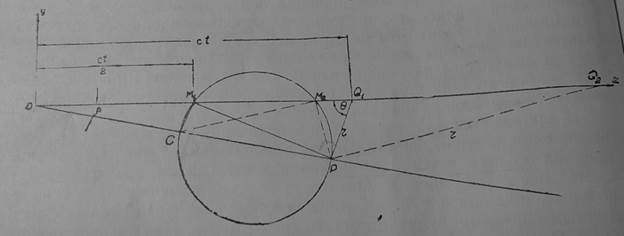
Рис.1

Результат этого построения дает возможность сформулировать следующий порядок нахождения положения возмущений, создающих в точке Р главную часть волн:

1) соединить Р с началом координат – точкой О;

2) разделить РО пополам, т.е. найти положение точки С;

3) построить окружность на РС, как на диаметре;

4) удвоить отрезки ОМ1 и ОМ2, образованные пересечением окружности с осью х, и, откладывая их от точки О, получить искомые положения центра возмущений. При этом построении возможны случаи, когда точек М может быть две, одна или эти точки отсутствуют. Если точка М одна, окружность касается оси х, тогда

т.е. предельное значение угла β, внутри которого возможно волнообразование, составляет 19°28´.

Если , то точки касания нет, волн в точке Р не возникает, и все волнообразование ограничено сектором с указанным предельным значением угла по обе стороны от оси х. Вид гребней волн получим, найдя кривые постоянной фазы; их определяет условие

,

Где – постоянная, причем r=PQ1 или r=PQ2, а или .

Найдем координаты х и у точки Р. Согласно рис. 1

, (2)

но , причем согласно (1)

,

тогда

и, следовательно, .

Исключая теперь время t из (2) , получаем уравнения кривых постоянной фазы в параметрической форме:

Вид кривых, соответствующих этим уравнениям:

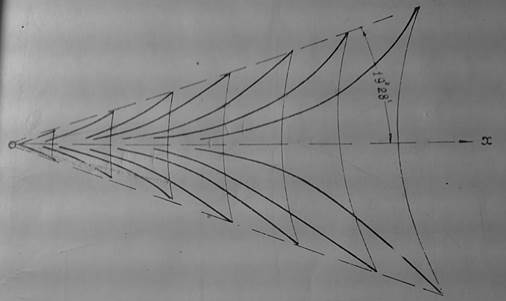
Найдем длину волн, возникающих при перемещении центра возмущений; она определится при из соотношения

Согласно этому равенству скорость бега волн, т.е. равна скорости перемещения источника возмущений, а сама формула совпадает с формулой, известной из теории малых волн для скорости распространения свободных волн.

Таким образом, при движении системы давлений по поверхности жидкости создаются две системы волн – поперечных и расходящихся.

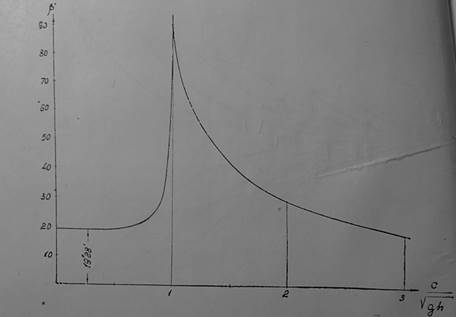
Если подсчитать высоты волн, то окажется, что в точке прило­жения точечного импульса давлений - они стремятся к бесконечности; это несоответствие можно устранить, взяв распределенное давление.

Высоты волн стремятся к бесконечности также в угловых точках; это есть следствие приближенности вида выражения . Можно показать, что поперечные волны создаются за счет центров Q2, а расходящиеся от центров Q1. При движении на глубокой воде угол зоны максимального распространения волн не зависит от скорости, и его величина остается постоянной; тот же порядок величины угла зоны расходящихся волн сохраняется и при движении судов на глубокой воде. При движении на мелкой воде угол, ограничивающий зону распространения волн, зависит от величины отношения , как указано на рис.2. Характерным является исчезновение поперечных волн при движении центра возмущений со скоростями, для которых ; в этом случае остаются только расходящиеся волны. Указанная картина наблюдается также при движении судов на мелкой воде и в мелководных каналах.