Название: Теорема Гауса

Вид работы: реферат

Рубрика: Физика

Размер файла: 87.59 Kb

Скачать файл: referat.me-341956.docx

Краткое описание работы: Реферат на тему: “Теорема Гауса” Цілі : Засвоєння та закріплення загальних відомостей про статичні електричні поля. Навчити розв’язувати задачі за допомогою використання теореми Гауса. Виховувати старанність, працелюбність.

Теорема Гауса

Реферат на тему:

“Теорема Гауса”

Цілі : Засвоєння та закріплення загальних відомостей про статичні електричні поля. Навчити розв’язувати задачі за допомогою використання теореми Гауса. Виховувати старанність, працелюбність.

Тип заняття : практичне

Хід заняття

Організація аудиторії

Нагадування щойно вивчених тем

Фронтальне опитування по них:

· закон збереження заряду (в ізольованій системі сумарний заряд не змінюється )

· релят. інваріантність заряду

· означення та зміст напруженості поля (сила, що діє на пробний заряд ) ; E =F /q;

· що виражає емпіричний закон Кулона

· принцип суперпозиції (наголошування на важливість векторних позначень )

· Розподіл зарядів ()

· Потік вектора Е ()

· теорема Гауса

Потік вектора Е скрізь замкнуту поверхню дорівнює алгебраїчній сумі зарядів обмежених цією поверхнею, поділеної на :

Приклад знаходження напруженості ел. поля нескінченно довгого тонкостінного циліндра

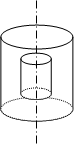Розв’язок:

У ході розв’язку треба наголошувати на причинах, за яких ми використовуємо теорему Гауса. Декілька раз підкреслювати, що поле має циліндричну симетрію.

Розбиття задачі на два етапи:

1) Знаходження поля всередині циліндра ()

Вибираємо точку на відстані від осі циліндра та проводимо крізь цю точку коаксіальний циліндр (рис. 1). Застосовуючи теорему Гауса, за відсутністю заряду всередині визначаємо, що

2) Знаходження поля зовні циліндра ()

Вибираємо точку на відстані від осі циліндра та проводимо крізь цю точку коаксіальний циліндр. Застосовуємо теорему Гауса. Потік крізь торці обраного циліндра дорівнює нулеві, а потік крізь бокову поверхню в теоремі Гауса набуде вигляду:

;

(1)

Приклад Знайти поле двох паралельних площин заряджених рівномірно різноіменими зарядами з густинами s та - s.

Розв’язок:

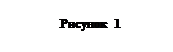
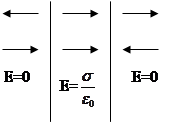Це поле легко знайти як суперпозицію полів, що створюються кожною площиною окремо. Між площинами напруженості полів що додаються мають однаковий напрямок, тому напруженість отримана для однієї площини (дивись лекцію) подвоїться, та результуюча напруженість поля між площинами має вигляд:

(2)

Зовні , легко побачити, що поле дорівнює нулю.

Поля систем розподілених зарядів .

Постійне втручання в індивідуальну роботу студентів

Слідкування за вірним напрямком ходу розв’язку

Індивідуальна робота по розв’язку задач: № 3.08, 3.10, 3.11, 3.14

Задача

Знайти поле нескінченного круглого циліндра, зарядженого рівномірно по поверхні, якщо подовжня густина - l.

Розв‘язок:

З точки зору симетрії поле має радіальний характер, так як вектор Е в кожній точці перпендикулярний до вісі циліндра, а модуль вектора напруженості залежить тільки від відстані r до вісі. Тоді замкнену поверхню треба обрати у формі коаксіального циліндру. В результаті по теоремі Гауса маю:

(3);

(4) (r>a), де а - радіус циліндру.

Коли r<a - E=0.

№3.08 Дано: q, R; E(0) - ?

Для даного напівкільця маємо:

(5)

(6)

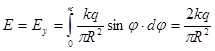
№3.10 Дано: q, R, -q; E(x) - ? x»R

Повідомити студентів, що у цьому випадку треба буде застосувати формулу наближеного числення для малих :

(7)

Користуючись розв’язком минулої задачі - формулою (6), згідно принципу суперпозиції полів, знаходимо:

(8)

(9)

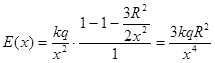
№3.11 Дано: R, q, ; F(x) - ?

(10)

Спираючись на отриманий на минулому занятті розв’язок задачі 3.9, та підставляючи його у формулу (10), отримаємо:

(11)

Теорема Гауса

Постійне втручання в індивідуальну роботу студентів

Слідкування за вірним напрямком ходу розв’язку

Індивідуальна робота по розв’язку задач: № 3.21, 3.22, 3.24

на вибір студента. Невирішені в аудиторії завдання - додому

№3.21 Напруженість електричного поля залежить тільки від Х та У як , де а – постійна, і та j – орти осей ОХ та ОУ. Знайти заряд у сфері радіусом R з центром у початку координат.

Розв’язок:

З теореми Гауса:

(12)

(13)

(14)

№3.22 Куля радіусу R має додатній заряд, об‘ємна густина якого залежить тільки від відстані r до її центру як r =, де - постійна, e=1. Знайти:

1) Модуль напруженості електричного поля в середині та зовні кулі як функцію від r.

2) Максимальне значення модуля напруженості та .

Розв’язок:

a) По теоремі Гауса:

У випадку r>R

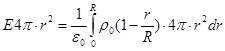
(15)

У випадку r<R

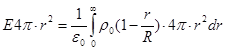
(16)

б) .

(17)

№ 3.24 Простір заповнено зарядом з об‘ємною густиною де та a - додатні постійні, r – відстань до центру системи. Знайти |E|=E(r).

Розв’язок:

З теореми Гауса:

(18) .

(19) .

Домашнє завдання

№ 3.16, 3.19, 3.22, 3.24

Надання ідейної думки до задачі №3.16: треба розбити сферу на кільця, що мають однакову напруженість поля.

Література

С.У. Гончаренко «Фізика 10»

А.В. Кругликов, С.О. Подласов «Збірник вправ та задач для довузівської підготовки з фізики»

И.Е. Иродов «Основные законы электромагнетизма»

И.Е. Иродов «Задачи по общей физике»

Справочник по физике для поступающих в ВУЗы под ред. Н.П. Калабухова

Студент-практикант : Філатов О.С.