Название: Вихровий характер магнітного поля

Вид работы: учебное пособие

Рубрика: Физика

Размер файла: 103.42 Kb

Скачать файл: referat.me-343678.docx

Краткое описание работы: Закон повного струму. Рівняння Максвелла для циркуляції вектора напруженості магнітного поля. Використання закону для розрахунку магнітного поля. Магнітний потік та теорема Гаусса. Робота переміщення провідника із струмом і контуру у магнітному полі.

Вихровий характер магнітного поля

РЕФЕРАТ

на тему:” Вихровий характер магнітного поля ”

План

1. Закон повного струму. Використання закону повного струму для розрахунку магнітного поля.

2. Магнітний потік. Теорема Гаусса для магнітного поля.

3. Робота переміщення провідника із струмом і контуру із струмом у магнітному полі.

4. Енергія магнітного поля.

1. Закон повного струму. Використання закону повного струму для розрахунку магнітного поля

Скористаємось рівнянням Максвелла для циркуляції вектора напруженості магнітного поля

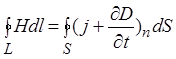, (1.1)

де j – густина струму провідності вільних електричних зарядів; - струм зміщення, не пов’язаний з наявністю вільних електричних зарядів; Н – напруженість магнітного поля.

У провідниках, в яких є вільні електричні заряди, струм зміщення відсутній (він може існувати лише у діелектричному середовищі), тобто

.

У цьому випадку рівняння (1.1) набуває вигляду:

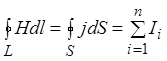. (1.2)

Рівняння (1.2) називається законом повного струму. Для написання закону повного струму через індукцію магнітного поля слід замінити Н у формулі (1.2) на

.

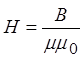Закон повного струму у цьому випадку матиме вигляд

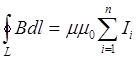. (1.3)

Рівняння (1.3) формулюється так:

Циркуляція вектора індукції магнітного поля уздовж довільного замкнутого контуру дорівнює алгебраїчній сумі всіх струмів, охоплених цим контуром і помноженій на ₀ .

Як видно з рівняння (1.3)

.

Таке магнітне поле називається вихровим. Силові лінії магнітного поля є завжди замкнутими.

Скористаємось законом повного струму (1.3) для розра-хунку магнітного поля соленоїда і тороїда.

а) знайдемо циркуляцію вектора В вздовж замкнутого контуру ABCD (рис.1). У нашому випадку витки в соленоїді щільно прилягають один до одного. Соленоїд має довжину, значно більшу за діаметр.

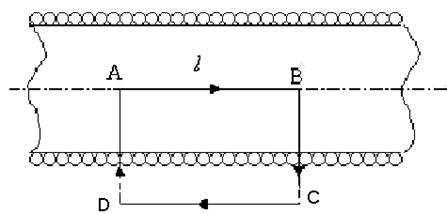
Рис.1

.

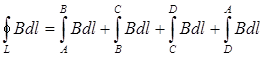На ділянках DA і BC 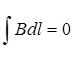; Тут а

На ділянці CD 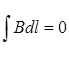; Цю ділянку можна вибрати досить далеко від соленоїда, де магнітне поле відсутнє.

Тому з урахуванням цих зауважень маємо:

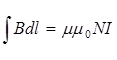. (1.4)

де N – число витків, які вкладаються в інтервалі довжини соленоїда АВ; І – струм, який протікає в цих витках.

Але 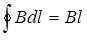, де l = AB. Закон повного струму в цьому випадку перепишеться:

. (1.5)

Звідки індукція магнітного поля на осі довгого соленоїда буде дорівнювати:

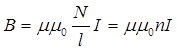. (1.6)

Вираз (13.1.6) показує, що на осі довгого соленоїда зі струмом І індукція магнітного поля дорівнює:

В = ₀ nI.

б) магнітне поле на осі тороїда.

Розглянемо тороїд, який має вигляд довгого соленоїда, кінець і початок якого збігаються (рис.13.2).

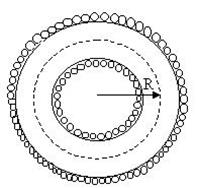
Рис.2

Витки в такій котушці щільно прилягають один до одного, а радіус осьової лінії R. Знайдемо циркуляцію вектора вздовж осьової лінії тороїда

,

де N - число витків у тороїді; І - струм у витках.

Але - довжина кола вздовж осьової лінії, тому

,

де - число витків на одиницю довжини осьової лінії тороїда.

Таким чином, індукція магнітного поля на осі тороїда визначається такою ж формулою, що і для довгого соленоїда, тобто

В = ₀ nI . (1.7)

2. Магнітний потік. Теорема Гаусса для магнітного поля

Потоком магнітної індукції або магнітним потоком називають скалярну величину, яка дорівнює:

, (2.1)

де - вектор індукції магнітного поля у напрямку нормалі до площадки dS (рис.13.3)

Рис.13.3

Повний магнітний потік через поверхню S знаходять шляхом інтегрування.

Магнітному потоку в 1 Вб відповідає 10⁸ силових ліній індукції магнітного поля крізь площадку в 1 м² .

У випадку замкнутої поверхні слід відрізняти між собою такі особливості:

- силові лінії, які входять у поверхню, мають від’ємний потік, тому в цьому випадку

- силові лінії, які виходять з поверхні мають

- у загальному випадку

. (2.2)

Вираз (2.2) є теоремою Гаусса для магнітного поля. Суть цієї теореми полягає в тому, що силові лінії магнітного поля не пов’язані з магнітними зарядами. Магнітних зарядів у природі не існує. Описане явище показане на рис. 4.

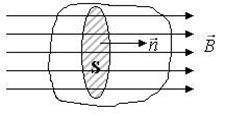
Рис.4

. (2.3)

3. Робота переміщення провідника із струмом і контуру із струмом у магнітному полі

Знайдемо роботу, яку слід виконати для переміщення провідника із струмом І у магнітному полі, як це показано на рис. 13.5

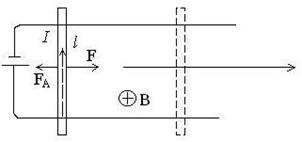
Рис.13.5

Провідник, що має довжину l і струм І виготовлений у вигляді коточка і має можливість переміщуватись. На рухому частину провідника з сторони магнітного поля діє сила Ампера, напрям якої визначається правилом лівої руки.

Для переміщення такого коточка вздовж направляючих дротів слід прикладати силу F, яка має бути рівною силі Ампера. Робота в цьому випадку буде дорівнювати:

. (13.3.1)

де F_A =IBl – величина сили Ампера, яка діє на рухомий коточок, тому:

A = -Ibldx = -IbdS = -Id (3.2)

Знак мінус показує, що робота виконується проти сили Ампера.

Якщо роботу виконує сила Ампера, то

A= Id (3.3)

де А – позитивна робота, виконана силою Ампера.

Після інтегрування одержуємо роботу сили по переміщенню провідника із струмом у магнітному полі.

A = -I,

або

A =I. (3.4)

У випадку контуру із струмом, який рухається у магнітному полі, слід враховувати як позитивну роботу, так і негативну роботу переміщення двох частин цього контуру (рис.13.6)

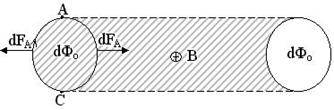
Рис.6

При русі частини контуру АС (зліва) робота виконується позитивна. Тому в цьому випадку

A₁ = I(d₁ + d₀ ), (3.5)

де dФ₁ – потік, який визначається площею лівої частини контуру АС (заштрихована площа),

dФ₀ - потік, який визначається площею самого контуру з струмом.

При переміщенні правої сторони цього контуру робота буде дорівнювати

A₂ = -I(d₂ + d₀ ), (3.6)

де dФ₂ – потік, який утвориться переміщенням правої частини контуру; dФ₀ – потік за рахунок площі самого контуру.

Ця площа перекривається площею правої сторони контуру. Робота А₂ – від’ємна

У загальному випадку робота переміщення контуру з струмом у магнітному полі буде дорівнювати

A = I(d₁ - d₂ )= Id. (3.7)

Після інтегрування одержимо

А=ІФ. (3.8)

Висновок. Робота переміщення провідника із струмом і контуру із струмом визначається однаковою формулою.

4. Енергія магнітного поля

Розглянемо замкнуте коло, в якому є резистор R, котушка L і джерело струму  (рис.7)

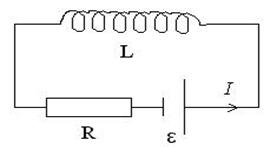
Рис.7

Скористаємось другим правилом Кірхгофа для замкнутого контуру, показаного на рис.7.

У цьому випадку

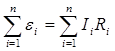, (4.1)

або

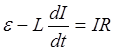, (4.2)

де - електрорушійна сила самоіндукції, діє лише в момент замикання або розмикання кола.

З рівняння (13.4.2) визначимо електрорушійну силу джерела

. (4.3)

Зведемо цей вираз до спільного знаменника

dt = Irdt + LdI . (4.4)

Помножимо вираз (13.4.4) на струм І, одержимо

Idt = I² rdt + LIdI , (4.5)

де I² rdt - джоулевe тепло; Idt - робота сторонніх сил джерела струму; LIdI - енергія магнітного поля, локалізована в котушці зі струмом.

Тому

dW_м = LIdI . (4.6)

Інтегруємо цей вираз у межах зміни енергії магнітного поля від 0 до W_м , а струму від 0 до І, одержимо

,

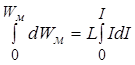або

. (4.7)

Вираз (13.4.7) визначає енергію магнітного поля котушки зі струмом.

Для довгого соленоїда L=₀ n² V. Підставимо це значення L у (13.4.7), одержимо

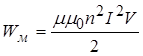. (4.8)

де ² ₀ ² n² І² =В² – квадрат індукції магнітного поля соленоїда.

З урахуванням цього зауваження одержуємо:

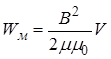. (4.9)

При діленні енергії магнітного поля на об’єм одержимо об’ємну густину енергії магнітного поля, локалізованого в котушці

,

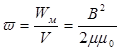або

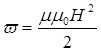. (4.10)