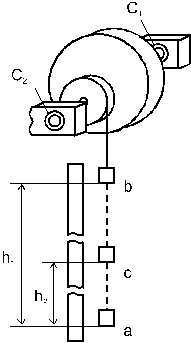Название: Закон сохранения энергии в механике

Вид работы: лабораторная работа

Рубрика: Физика

Размер файла: 75.03 Kb

Скачать файл: referat.me-342006.docx

Краткое описание работы: Лабораторная работа № 2а ПРОВЕРКА ЗАКОНА СОХРАНЕНИЯ ЭНЕРГИИ В МЕХАНИКЕ. Основы метода Система тел, на которую не действуют внешние силы, называется замкнутой. В замкнутой системе учитываются только внутренние силы, т.е. силы взаимодействия между входящими в эту систему телами.

Закон сохранения энергии в механике

Лабораторная работа № 2а

ПРОВЕРКА ЗАКОНА СОХРАНЕНИЯ ЭНЕРГИИ В МЕХАНИКЕ.

Основы метода

Система тел, на которую не действуют внешние силы, называется замкнутой. В замкнутой системе учитываются только внутренние силы, т.е. силы взаимодействия между входящими в эту систему телами.

Внутренние силы могут быть консервативными и неконсервативными (диссипативными).

Консервативными называются силы, работа которых не зависит от вида и длины траектории тела, а определяются лишь координатами начала и конца траектории. В системе тел, где действуют лишь консервативные силы, нет перехода механического движения в другие виды движения или превращения других форм движения в механическое. К консервативным силам относятся гравитационные, упругие, кулоновские.

Неконсервативными называются силы, работа которых зависит от вида и длины траектории. Таковыми являются силы трения, силы, возникающие при неупругой деформации. Наиболее общей мерой различных форм движения материи является ее энергия. Энергия характеризует способность тел совершать работу. Различают два вида механической энергии - кинетическую Е_К и потенциальную Е_Р .

Кинетическая энергия тела - это энергия движения. При поступательном движении кинетическая энергия тела массы m, движущегося со скоростью V, равна:

(1)

При вращательном движении твердого тела роль массы играет момент инерции I, роль линейной скорости - угловая скорость w. Кинетическая энергия тела, вращающегося вокруг неподвижной оси, равна:

(2)

Потенциальная энергия - это энергия, зависящая от взаимного расположения взаимодействующих тел или частей одного и того же тела. Потенциальная энергия в поле силы тяжести Земли выражается формулой:

(3)

Полная механическая энергия системы равна сумме ее кинетической и потенциальной энергии.

Рис.1

Изменение полной механической энергии системы равно суммарной работе всех внешних сил и всех внутренних неконсервативных сил и всех внутренних неконсервативных сил:

D(E_K + E_P ) = A_ВНЕШ + А_НЕКОНС (4)

Из (4) следует, что если система замкнута (А_ВНЕШ = 0) и консервативна (А_НЕКОНС = 0), то полная механическая энергия системы не изменяется:

D(E_K + E_P ) = 0 или E_K + E_P =const (5)

Это утверждение составляет содержание закона сохранения механической энергии, который формулируется так: полная механическая энергия замкнутой консервативной системы сохраняется неизменной.

Для проверки закона сохранения механической энергии в данной работе применяется установка, состоящая из махового колеса, насажанного на вал, и отсчетной линейки (Рис.1). Вал установлен на шарикоподшипниках С₁ и С₂ . На шкив вала намотан шнур, к концу которого крепится груз массой m. Опускаясь под действием силы тяжести, груз приводит во вращение вал с маховиком.

Если в результате движения до полного разматывания шнура груз проходит расстояние h₁ , то это означает, что в начальном положении система обладала запасом энергии E_Р = mgh₁ .

Потенциальная энергия поднятого груза E_Р расходуется на преодоление трения А_ТР и увеличение кинетической энергии системы.

По закону сохранения энергии в механической замкнутой системе получим уравнение:

(6) ,

где: - кинетическая энергия груза;

- кинетическая энергия махового колеса; А_ТР - работа по преодолению сил трения.

Правая часть уравнения (6) относится к тому моменту времени, когда груз находится в наиболее низком положении.

Цель работы:

проверить справедливость уравнения (6). Для этого нужно определить значения величин, входящих в уравнение.

Из известных формул скорости и пути равноускоренного движения легко найти выражение для скорости V:

(7)

Угловая скорость вала с маховиком находится по формуле:

(8),

где: r - радиус шкива.

Момент инерции махового колеса может быть вычислен по формуле:

(9)

где: M = p×R² ×r×a - масса махового колеса; R, r, a- соответственно радиус, плотность материала и толщина махового колеса.

Работу по преодолению сил трения можно вычислить, исходя из следующих соображений. Вращаясь по инерции, маховое колесо поднимает груз на высоту h₂ < h₁ . При этом система будет обладать потенциальной энергией mgh₂ , кинетическая энергия системы будет равна нулю. Убыль энергии системы при переходе из состояния b в состояние с равна работе по преодолению сил трения:

mgh₁ - mgh₂ = M_ТР j (10),

где M_ТР - момент сил трения;

j - общий угол поворота маховика с валом за время вращения в радианах.

Угол поворота связан с перемещением груза формулой:

(11)

Решая совместно (10) и (11), найдем М_ТР :

Принимая, что момент сил трения постоянен по величине, найдем работу сил трения в уравнении (6):

(12)

где: h₁ = b - a; h₂ = c - a.

Получаем рабочую формулу:

(13)

где: d - диаметр шкива; D - диаметр махового колеса.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. Определить по отсчетной линейке нижнее положение груза “а”.

2. Поднять груз в исходное верхнее положение и взять по линейке отсчет “b”.

3. Измерить секундомером время t отпускания груза из положения “b” в положение “a”.

4. Определить уровень “с”, на который груз поднимается по инерции.

5. Повторить опыт не менее 5 раз.

6. Рассчитать величины E_К1 , E_К2 , А_ТР , E_Р по формулам (6)-(9), (12).

7. Результаты измерений и вычислений занести в таблицу по предложенной форме 1.

Форма 1

№ опыта	a, м	b, м	c, м	t, с	m, кг	M, кг	d, м	D, м	g, м/с2
1.
…
5.

8.Проверить справедливость уравнения (13) для каждого опыта.

Расчёт величин Е_К1 , Е_К2 , А_ТР , Е_Р по формулам (6)-(9) и (12).

После того, как рассчитаны значения Е_Р и Е в каждом отдельном опыте, рассчитайте их средние значения <Е_Р > и <Е>.

СТАТИСТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ.

Пусть в результате измерений какой-либо физической величины получено ограниченное множество значений {x_i }. Используя ПМК для заданного рода значений можно вычислить статистические характеристики массива. Программа “Среднее-2” вычисляет среднее <x>, среднеквадратичное отклонение S_П , а также доверительный интервал Dx.

Для вычисления доверительного интервала используются так называемые t - квантили распределения Стьюдента. Для коэффициента надёжности a = 0.8 и числа измерений n > 7 t-квантили апроксимируются выражением вида:

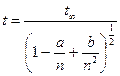
где: a, b и t зависят от заданного значения коэффициента надёжности a.

например, для a = 0.95; t = 1.96; a = 2.387; b = 1.260. С помощью t значение ширины доверительного интервала Dx и его границ x_НИЖ, x_ВЕРХ выражаются

формулами

,

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

1. Какие силы называются консервативными? Является ли консервативной система тел, рассматриваемая в данной работе?

2. Дайте определение кинетической и потенциальной энергии механической системы.

3. Сформулируйте закон сохранения энергии в механике.

ЛИТЕРАТУРА

1. И.В.Савельев. Курс общей физики. Т.1 - М.:Наука, 1977, §§ 18-24.