Дослідне вивчення властивостей математичного маятника

Лабораторна робота № 7.

ДОСЛІДНЕ ВИВЧЕННЯ ВЛАСТИВОСТЕЙ МАТЕМАТИЧНОГО МАЯТНИКА.

Мета роботи : Перевірити справедливість формули періоду коливань математичного маятника для різних довжин маятника і різних кутів відхилення від положення рівноваги.

Прилади і матеріали : Штатив, сталева кулька на нитці, рулетка, секундомір, транспортир.

Теоретичні відомості .

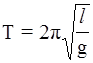Математичним маятником називається матеріальна точка, підвішена на невагомій нерозтяжній нитці. Гарним наближенням до цієї моделі є маленька кулька, підвішена на тонкій міцній нитці (тонка сталева дротина, рибальська волосінь, тощо). Як було показано в курсі фізики, при відхиленні маятника на малий кут він буде здійснювати гармонічні коливання. Період цих коливань визначається виразом:

(1)

де l - довжина маятника.

В даній роботі пропонується перевірити справедливість формули (1) для різних довжин і різних кутів відхилення.

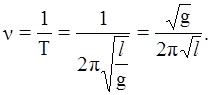Оскільки частота коливань ν обернена до періоду Т, то з формули (1) одержимо:

(2)

З (2) випливає, що добуток частоти маятника ν на корінь квадратний з його довжини повинен бути сталою величиною:

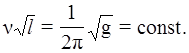(3)

Якщо g=9,81то ця константа дорівнює (0,4985±0,0005).

Хід роботи .

Завдання 1. Дослідження залежності частоти коливань математичного маятника від його довжини.

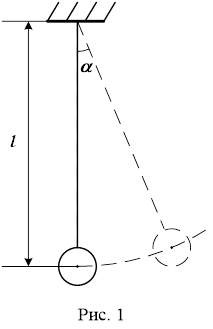1. Змінюючи довжину нитки, встановіть її приблизно рівною 1м. Ретельно виміряйте довжину маятника l - це відстань від точки підвісу до центра кульки (див. рис.1). Під час вимірювання намагайтесь забезпечити точність 1-2мм. Оскільки довжину близько 1м одному вимірювати незручно, то запросіть на допомогу ще одного студента.

2. Відхиліть маятник від положення рівноваги на кут =3−5˚ і відпустіть маятник. Пропустіть декілька коливань і з рахунком "нуль" включіть секундомір. Зручно включати секундомір в момент, коли маятник перебуває в положенні максимального відхилення. Виміряйте час t для 30−50 коливань.

3. Повторіть дослід ще один раз.

4. Зменште довжину маятника приблизно вдвічі і повторіть вимірювання довжини і часу.

5. Ще раз зменште вдвічі довжину маятника, виміряйте її і визначте час 50 коливань. Оскільки період коливань зменшується, то для підвищення точності вимірювань число коливань слід збільшити.

6. Для кожного досліду обчисліть частоту , і добуток . Результати вимірювань і обчислень зручно подати у виді таблиці 1.

Табл.1.

№	l, м	N	t, с	ν, с-1
1
2
3

Завдання 2. Дослідження залежності частоти коливань маятника від амплітуди його коливань.

1. Встановіть довжину маятника рівною приблизно 1м. Виміряйте довжину маятника і визначте час 30−50 коливань, як це описано в п.п.1 і 2 завдання 1.

2. Обчисліть частоту коливань маятника, одержану з досліду (експериментальну):

3. Повторіть визначення частоти для кутів відхилення 20˚, 40˚ і 60˚ від вертикалі. Оскільки при великих кутах відхилення стабільність коливань зменшується, то можна обмежитись меншим числом коливань (але не менше 20).

4. Обчисліть теоретичну частоту ν коливань маятника за формулою (2) . Візьміть = 3,1416 і g = 9,81

5. Знайдіть відносне відхилення результатів експерименту від теоретичного значення:

6. Результати вимірювань і обчислень зручно подати у вигляді таблиці 2.

Табл.2

№	l, м		N	t, с	νе ,с-1	ν, с-1	E,%
1
2
3
4

7. Зробіть висновки до кожного з завдань.

Контрольні запитання.

1. Які коливання називають гармонічними?

2. При яких умовах виникають механічні гармонічні коливання?

3. Чи підтвердив експеримент передбачену теорією залежність частоти коливань математичного маятника від його довжини?

4. Чи відрізняється частота коливань маятника при великих кутах відхилення від теоретичного значення, обчисленого за формулою (2)?