Название: Изучение физического маятника

Вид работы: контрольная работа

Рубрика: Физика

Размер файла: 53.11 Kb

Скачать файл: referat.me-343889.docx

Краткое описание работы: Изучение законов колебательного движения на примере физического маятника. Определение механических, электромагнитных и электромеханических колебательных процессов. Уравнение классического гармонического осциллятора и длины математического маятника.

Изучение физического маятника

Министерство образования РФ

Рязанская государственная радиотехническая академия

Кафедра ОиЭФ

Контрольная работа

"Изучение физического маятника"

Цель работы: изучение законов колебательного движения на примере физического маятника.

Приборы и принадлежности: маятник универсальный ФПМ04.

Элементы теории

Колебания - это процессы (движения или изменения состояния), в той или иной степени повторяющиеся во времени.

Колебательные процессы разделяют на механические, электромагнитные, электромеханические и т.д.

Механические колебания – колебания физических тел (маятников, струн, частей механизмов и т.д.); электромагнитные – колебания величин показывающих состояние электромагнитного поля (переменного электрического тока в цепи, колебания векторов напряженности и магнитной индукции переменного электромагнитного поля); электромеханические - колебания физических тел под действием электромагнитных полей (мембраны телефона, диффузора электродинамического громкоговорителя и т.д.)

Колебательная система – система совершающая колебания.

Любые колебания могут быть свободными или вынужденными.

Свободные колебания или собственные колебания – есть колебания, которые происходят в отсутствии переменных внешних воздействий на колебательную систему и возникает при однократном отклонения системы от состояния ее устойчивого равновесия.

Вынужденные колебания – есть колебания, возникающие, в системе под влиянием переменного внешнего воздействия.

Гармонические колебания подчиняются по закону:

1) ,

где A- амплитуда колебаний; w₀ = 2p/Т - круговая частота; Т - период; t - время; a - начальная фаза колебаний; (w₀ + a) – фаза колебаний.

Функция x(t) в (1) представляет собой решение дифференциального уравнения свободных колебаний:

2) ; .

Физическая система, выведенная из состояния равновесия и предоставленная самой себе, в которой изменение одного из параметров описывается дифференциальным уравнением (2), называется классическим гармоническим осцилятором.

Физический маятник - любое твёрдое тело которое под действием силы тяжести может свободно качаться вокруг неподвижной горизонтальной оси, не проходящей через центр масс. Движение маятника описывается уравнением:

3) ,

где I - момент инерции мятника; j - угол отклонения маятника от положения равновесия; t – время; M – момент действующих на маятник сил.

В данной работе в качестве физического маятника используется однородный стальной стержень дайны l. На стержне закреплена опорная призма, острое ребро которой является осью качения маятника. Призму можно перемещать по стержню. Пусть расстояние от оси качения маятника до его центра масс равно b.

4) ,

где - момент инерции стержня относительно оси, проходящей через его середину, m - масса маятника.

Момент силы тяжести, действующей на маятник:

5) .

Знак "минус" ставится так, как направление действия возвращающей силы и j всегда противоположны.

В данном случае моментом силы трения можно пренебречь. Подставляя выражения для I и M в (4) получаем уравнение:

6) , где

7) .

Решением данного уравнения является функция:

8) j(t) = j₀ sin(w₀ t + a).

Амплитуда j₀ и фаза aзависят от того, как возбуждаются колебания маятника.

Период колебаний T = 2p/w₀ равен:

9) .

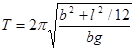Период колебаний физического маятника не зависит ни, от фазы, ни от амплитуды колебания. Это утверждение справедливо для колебаний, подчиняющихся уравнение (7). Движение маятника описывается этим уравнением приближенно - в той мере, в какой справедлива использованная при выводе (7) формула sin(j) »j. Исследование правильности утверждения о том, что период колебаний маятника независит от амплитуды, является чувствительным методом проверки теории. Как известно, период колебаний математического маятника определяется формулой:

10) 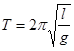, где l - длина математического маятника.

Поэтому величина

11)

называется приведенной длиной физического маятника. Точку О’, отстоящую от точки опоры O на расстояние l_пр , называют центром качания физического маятника, Можно доказать, что точка опоры и центр качания маятника обратимы, т.е. при качании маятника вокруг точки O период должен быть таким же, как и при качании вокруг точки O’. Исследование справедливости этого утверждения является другим методам проверки теории. Ещё один метод заключается в проверке правильности формулы (9). Величину b можно изменять, передвигая опорную призму по стержню.

В данной работе в качестве математического маятника используется металлический шарик, подвешенный на двух расходящихся нитях, длину которых можно изменять.

Расчётная часть

После работы с установкой имеем все данные, которые занесены в таблицу и длину физического маятника l_изм = 0,6 м.

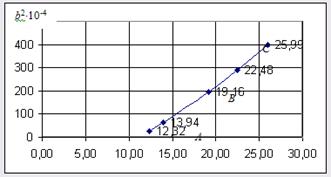
Теперь построим график зависимости T² b от b² .

Физический маятник
№	N	b1 ×10-2 м	ti1 , с	, с	, с
1	40	5	63,12	62,98	1,57
2			62,87
3			62,96
№	N	b2	ti2 , с	, с	, с
1	40	8	53,01	53	1,32
2			52,95
3			53,03
№	N	b3	ti3 , с	, с	, с
1	40	14	46,76	46,81	1,17
2			46,81
3			46,85
№	N	b4	ti4 , с	, с	, с
1	40	18 Пересчитывай	46,06	46,01	1,15
2			46,01
3			45,95
№	N	b5	ti5 , с	, с	, с
1	40	20	45,54	45,64	1,14
2			45,78
3			45,61
2			44,97
3			45,07

Возьмём несколько точек на графике и найдём по их параметрам (T² b и b² ) значения и для данных точек.

; ;

Для точки A:

;;

Для точки B:

;;

Для точки С:

;;

По найденным значениям величин и для точек А, В, С найдём их средние значения:

;;

Отсюда найдём значения g (ускорения свободного падения) и l (реальная длина маятника).

= 10,09 м/с² . l = 0,57 м.

Найденное значение l примерно равняется l_изм .

Теперь оценим погрешность величины g.

Выражая g из формулы (9) получим формулу вида: .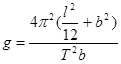

Вычисление g по данной формуле допускает определение погрешности вычисления величины g по упрощённой формуле.

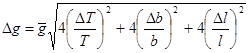; ; ; при DT = Dt имеем:

;

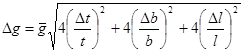Для нахождения абсолютной погрешности Dg, найдём погрешности величин найденных прямыми измерениями: Dt, Db и Dl.

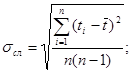
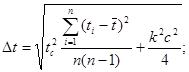
при t_c = 1,96, k = 1.1(для P = 0,95) и с = 10^-3 с.

с.

Так как различные длины b_i измерялись по одному разу (D_сл » 0).

при k = 1.1(для P = 0,95) и с = 10^-3 м.

м.

Значение Dl = Db, т.к. l измерялось тем же измерительным инструментом и 1 раз, как и b.

м.

Теперь подставим значения абсолютных погрешностей Dl, Db и Dt в формулу расчёта Dg:

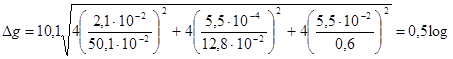м/с² .

g = 10,1±0,5 м/с² .

Далее по формуле (11) найдём приведённую длину физического маятника l_пр .

м.

Найденное значение приведённой длины l_пр равняется длине математического маятника.