Название: Решение задач по сопротивлению материалов
Вид работы: контрольная работа
Рубрика: Физика
Размер файла: 274.29 Kb
Скачать файл: referat.me-343544.docx
Краткое описание работы: Задание Дано: Определить силу Q Решение Составим уравнение работ, выражающее принцип возможных перемещений: Уравнение работ, выражающее принцип возможных перемещений:
Решение задач по сопротивлению материалов
Задание .
Дано: ![]() ;
;
![]() ;
; ![]() ;
;
![]()
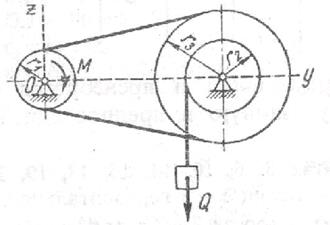
Определить силу Q
Решение
Составим уравнение работ, выражающее принцип возможных перемещений:
![]()
Уравнение работ, выражающее принцип возможных перемещений:
![]() (1)
(1)
Скорость точки А равна скорости точки B
![]()
Тогда
![]()
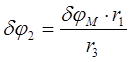
Перемещение груза Q
![]()
Подставив в уравнение (1) выражения возможных перемещений точек системы, получим
![]()
Откуда
![]()
X=C2 t2 +C1 t+C0
При t=0 x0
=8 ![]() =6
=6
t2 =4 x2 =40 см
X0 =C2 t2 +C1 t+C0
8=0+0+C0
C0=8
V=x=2C2 t+C1
6=0+C1
C1 =6
X2 =C2 t2 2 +C1 t2 +C0
40=C2 *42+6*4+8
40-32=C2 *42
8=C2 * 14
C2 =0,5
2) При t=t1 , t1 =2
C0 =x0
C1 =V0
C2 =x2-C1 t-C0 /t2
3)C0 =8
C1 =6
C2 =0,5
X=0,5t2 1 +6t1 +8
![]() =V=t+6
=V=t+6
a=![]() =1
=1
V=r2
![]() 2
2
R2
![]() 2
=R3
2
=R3
![]() 3
3
![]() 3
=V*R2
/(r2
*R3)
=100(t+6)/60*75=0,02(t+6)
3
=V*R2
/(r2
*R3)
=100(t+6)/60*75=0,02(t+6)
Vm
=r3
*![]() 3
=75*0,177=13,3
3
=75*0,177=13,3
at
m
=r3
![]()
![]() =0,02t
=0,02t
at
m
=R3
![]() =75*0,02t=1,6t
=75*0,02t=1,6t
an
m
=R3
![]() 2
3
=75*0,02(t+6)=1,6(t+6)2
2
3
=75*0,02(t+6)=1,6(t+6)2
a=![]()
![]()
Вариант 3 Д1
Дано: ![]()
![]()
![]()
![]()
![]()
![]() Определить
Определить ![]() и
и ![]() .
.
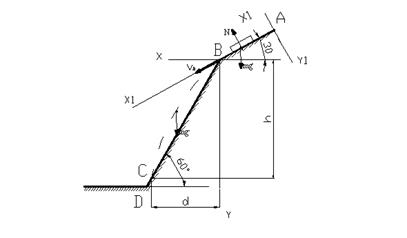
Решение
m![]() =
=![]()
1) m![]() =
=![]()
OZ: m![]() = -Q+R+Psin
= -Q+R+Psin![]()
![]() =
=![]() ; P=mg; R=0,5
; P=mg; R=0,5![]() ;
;
m![]() = -Q+0,5
= -Q+0,5![]() +mg sin
+mg sin![]() | :m
| :m
![]() = -
= -![]() +
+![]() +g sin
+g sin![]()
![]() =
=![]() =
=![]()
![]()
![]()
![]() =
=![]() 104
104
![]() =
=![]()
![]()
![]() =
=![]()
![]()
н.у: ![]() =10 м/c; l=4;
=10 м/c; l=4;
С=![]() =
=![]() 2,16
2,16
![]() =
=![]()
![]() =
=![]() 4 м/c
4 м/c
2) m![]() =
=![]()
OY: N=Pcos![]() =
=![]()
OX: m![]() =
=![]() =
=![]() =
=
![]()
![]()
![]() =
=![]() | :m
| :m
![]() =
=![]() =
=![]() =
=
![]()
![]() = -
= -![]()
![]() =0,375cos2
=0,375cos2![]() -10,2t+C
-10,2t+C![]()
н.у: t=0; ![]() =4 м/с;
=4 м/с;
C![]() = 4-0,375=3,625
= 4-0,375=3,625
![]() =0,375cos2
=0,375cos2![]() -10,2t+3,625
-10,2t+3,625
![]() ;
; ![]() =0,375cos2t-10,2t+3,625
=0,375cos2t-10,2t+3,625
![]() =
=![]()
x=0,2sin2t-5,1![]() +3,625t+C
+3,625t+C![]()
н.у: ![]() =0;
=0; ![]() =0; => C
=0; => C![]() =0
=0
Ответ:
x=0,2sin2t-5,1![]() +3,625
+3,625
Вариант № 3. Определение реакций опор твердого тела
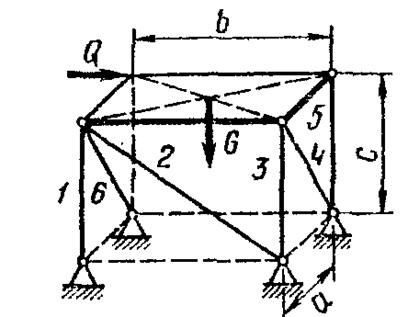
Найти реакции опор конструкции
| Силы, кН |
Размеры, см |
|||
| Q |
G |
a |
b |
c |
| 20 |
18 |
400 |
400 |
450 |
К раме ABCD, закрепленной при помощи стержней на шарнирах, приложены: масса G, сила Q. Для нахождения реакций опор твердого тела нужно найти силу, действующую на стержни, крепящие раму ABCD. Обозначим их как ![]() .
.
У нас 6 неизвестных, поэтому мы должны составить 6 уравнений.
Для того, чтобы рама находилась в равновесии необходимо и достаточно, чтобы сумма проекций сил на оси и моментов равнялись нулю.
Составим систему:
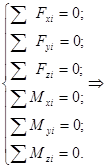
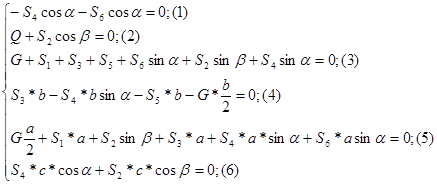 ,
,
где 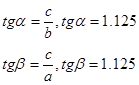
![]() .
.
Из уравнения (2) найдем значение ![]() :
:
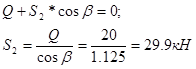
Из уравнения (6) найдем значение ![]() :
:
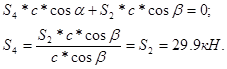
Из уравнения (1) найдем значение ![]() :
:
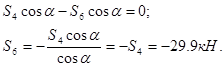
Из уравнения (4) выразим ![]() :
:
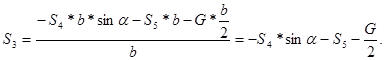 (7)
(7)
Из уравнения (5) выразим ![]() :
:
![]()
Так как ![]() имеем:
имеем:
![]()
(8)
Уравнения (7) и (8) приравняем:
![]() (9)
(9)
Из уравнения (9) выразим ![]() :
:
![]() (10)
(10)
Из уравнения (3) выразим ![]() :
:
![]()
Так как ![]() имеем:
имеем:
![]() (11)
(11)
Подставим уравнение (8) в уравнение (11), получим:
![]()
![]() (12)
(12)
Приравняем уравнения (10) и (12):
![]() (13)
(13)
Выразим из уравнения (13) ![]() :
:
![]()
![]()
Так как ![]() имеем:
имеем:
![]() (14)
(14)
Подставляя значения в уравнение (14) находим ![]() :
:
![]()
Подставим найденное значение ![]() в уравнение (8) найдем
в уравнение (8) найдем ![]() :
:
![]()
Из уравнения (12) найдем значение ![]() :
:
![]()
Результаты вычислений приведены в таблице:
|
|
|
|
|
|
|
| 71,252 |
29,9 |
80,196685 |
29,9 |
-31 |
-29,9 |
Знак «-» в значениях реакций означает, что реакции направлены в противоположную сторону от предполагаемой.
Похожие работы
-
Действие физических сил на конструкцию
Определение реакций опор составной конструкции по системе двух тел. Способы интегрирования дифференциальных уравнений. Определение реакций опор твердого тела. Применение теоремы об изменении кинетической энергии к изучению движения механической системы.
-
Расчет элементов статически неопределенных и статически определенных систем на прочность, жесткость
Введение Все твердые тела в той или иной степени воспринимают воздействие внешних сил без разрушения и существенного изменения геометрических размеров и формы, то есть обладают свойствами прочности и жесткости.
-
Параметры точек твердого плоскодвижущегося тела
Задание К-5-27. Определение скоростей и ускорений точек твердого тела при плоском движении ώOA ώI ξOA 15 cm 60 cm/c 30 cm/c2 Условие скорости звена:
-
Нахождение значений физических величин
Определение количества воды, которое необходимо дополнительно подать в трубопровод, чтобы давление в нем поднялось до значения по манометру. Оценка абсолютного и вакуумметрического давления в сосуде. Равнодействующая сила воздействия воды на стенку.
-
Теоретическая механика (шпаргалка)
Статика Уравновешенные силы: Система сил, под действием которой свободное твердое тело может находится в покое, называется уравновешенной. Аксиомы статики:
-
Определение величин по теоретической механике
Определение поступательного и вращательного движения твердого тела. Кинематический анализ плоского механизма. Применение теоремы об изменении кинетической энергии к изучению движения механической системы. Применение общего управления динамики к движению.
-
Центр скоростей и ускорение плоскодвижущегося шатуна
Расчет мгновенного центра скоростей и центростремительного ускорения шатуна, совершающего плоское движение. Определение реакции опор для закрепления бруса, при котором Ма имеет наименьшее значение. Нахождение модуля ускорения и модуля скорости точки.
-
Задача по Физике
С помощью принципа возможных перемещений (общего уравнения динамики) определить ускорение центра масс тела А. С помощью принципа Даламбера найти натяжение нити на всех участках. Рассмотрев динамическое равновесие последнего тела, сделать проверку правильности выполненных расчётов.
-
Плоская задача теории упругости
Нижегородский государственный архитектурно-строительный университет. Кафедра сопротивления материалов и теории упругости. Расчетно-проектировочная работа
-
Прикладная механика
Задача 1 Для стального трубчатого вала , который оборачивается с постоянной угловой скоростью, требуется: Определить, пренебрегая трением в подшипниках, мощность на шкиве P0 .