Название: Составление уравнений равновесия и расчет действующих сил

Вид работы: реферат

Рубрика: Физика

Размер файла: 292.24 Kb

Скачать файл: referat.me-343568.docx

Краткое описание работы: Задача С 1 Жестяная рама закреплена в точке А шарнирно, а в точке В прикреплена к шарнирной опоре на катках. На раму действуют пара сил с моментом М = 100H*м и две силы F1 = 10H под углом 30 к горизонтальной оси, приложенная к точке K, и F4=40H под углом 60 к горизонтальной оси, приложенная к точке H.

Составление уравнений равновесия и расчет действующих сил

Задача С 1

Жестяная рама закреплена в точке А шарнирно, а в точке В прикреплена к шарнирной опоре на катках. На раму действуют пара сил с моментом М = 100H*м и две силы F₁ = 10H под углом 30° к горизонтальной оси, приложенная к точке K, и F₄ =40H под углом 60° к горизонтальной оси, приложенная к точке H.

Определить реакции связей в точках A и В, вызываемые заданными нагрузками. При окончательных подсчетах принять l = 0,5 м

2 ll

Дано : X_A F₄ ^’ X

М = 100 Н * м AH

F₁ = 10 Н F₄ ^’’ F₄ F₁ ^’’ F₁ l

£ ₁ = 30°K

F ₄ = 40 HF₁ ^’

L = 0,5 мМ 3l

£ ₄ = 60°2l

R_B

X_А, Y_А, R_B Д

Рис. С 1.0.

Решение:

Рассмотрим равновесие рамы. Проведем координатные оси XY (начало координат в точке А). На раму действуют следующие силы: 1 и 4, пара сил моментом М и реакция связи A, A, B (реакция неподвижной шарнирной опоры А изображаем двумя ее составляющими, реакция шарнирной опоры на катках направлена перпендикулярно опорной плоскости).

Составляем три уравнения равновесия:

1) ∑ FKX=0; XA+F4*coς 60 °+ F1*coς 30 °=0

2) ∑ FKY=0; YA-F4*ςin 60 °+ F1* ςin 30 °+RB=0

3) ∑ MA (FK)=0; -F4*ςin 60 °*2l+ F1* ςin 30 °*3l+F1* coς 30 °*l-M+RB*5l=0

Из уравнений (1) находим XA:

XA= -F4* coς 60 °-F1* coς 30 °= -40*0,5-10*0,866= -28,66H

Из уравнения (3) находим RB:

RB==

==

=49,12H

Из уравнения (2) находим YA:

YA=

Проверка:

- все силы реакции найдены правильно:

Ответ:

Задача С 2

Однородная прямоугольная плита весом P=5kH со стороны АВ=3l, ВС=2l закреплена в точке А сферическим шарниром, а в точке В цилиндрическим шарниром (подшипником) и удерживается в равновесии невесомым стержнем СС! На плиту действуют пара сил с моментом М=6лН*м, лежащая в плоскости плиты, и две силы. Значения этих сил, их направления и точки приложения Н, £1=90°с, Д, £2=30°с; при этом силы и лежат в плоскостях, параллельных плоскости xy, сила - в плоскости, параллельной xz, сила - в плоскости параллельной yz. Точки приложения Д и Н находятся в серединах сторон плиты. Определить реакции связей в(.) А и В, С. При окончательных расчетах принять l=0,5м.

С1

Z

Дано:

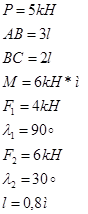
Y

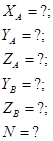
Рис С 2.0.

Решение:

1) Рассмотрим равновесие плиты. На нее действуют заданные силы: пара сил с моментом М, а также реакции связей. Реакцию сферического шарнира разложим на 3 составляющие: цилиндрического шарнира (подшипника) - на две составляющие: (в плоскости перпендикулярной оси подшипника), реакцию стержня направим вдоль стержня, предполагая, что он растянут (рис. С 2.0.)

2) Для определения составляем равновесия, действующей на плиту пространственной системы сил:

(1)

(2)

(3)

(4)

(5)

(6)

Из уравнения (4) находим N:

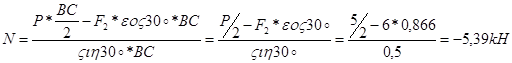
Из уравнения (5) находим ZB:

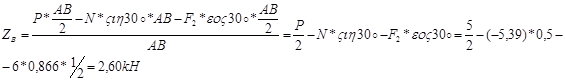
Из уравнения (1) находим XA:

Из уравнения (6) находим YB^

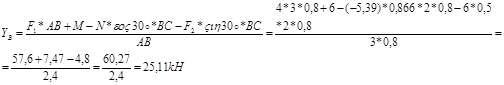
Из уравнения (2) находим YA:

Из уравнения (3) находим ZA:

Ответ:

XA= -1,67kH

YA= -29,11kH

ZA= -0,10kH

YB=25,11kH

ZB=2,60kH

N= -5,39kH

Знаки указывают, что силы направлены противоположно показанным на рис. С 2.0.

Задача К1

Дано:

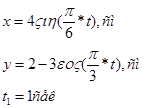
Три движения точки на плоскости

Найти:

- уравнение траектории точки

для момента времени

y

B

x

Рис. К 1.0.

Решение:

1) Для определения уравнения траектории исключим из заданных уравнений движения время t:

(1)

Преобразуя систему (1), получим:

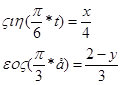(2)

Поскольку время е входит в аргументы тригометрических функций, где один аргумент вдвое больше другого, используем формулу: то есть:

Итак, получаем:

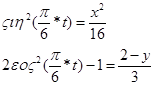(3)

Преобразуя систему (3), получим:

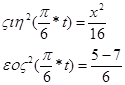(4)

Преобразуем:

Упрощая выражение, получим:

(5)

Выражение (5) – это уравнение траектории точки. График – парабола с вершиной в точке (0;11) на рис. К.1.0 а

2) Скорость точки найдем по ее траектории на координатной оси:

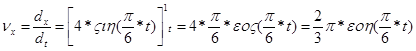см/с

y

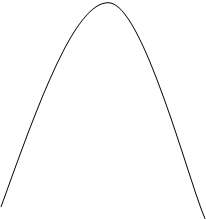(0;11)

y=-0,375x² +11

(-5,4;0)(5,4;0)

x

Рис. К 1.0 а

При t=1 сек, находим

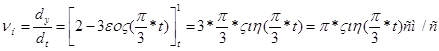
При t=t1=1 сек, находим

Находим скорость точки:

3) Аналогично найдем уравнение точки:

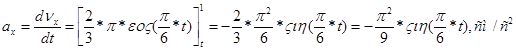
При t=t1=1 сек, находим

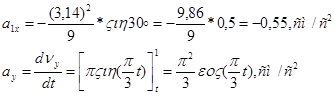
При t=t1=1 сек, находим:

Находим ускорение точки:

Найдем касательное ускорение, дифференцируя по времени равенства:

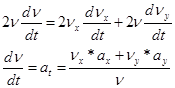
Учитывая найденные значения при t= 1 сек, получим:

5)Нормальное ускорение определяется по формуле:

6)Радиус кривизны траектории определяется по формуле:

Ответ:

a1=1,73 см/с2

aT=1,07 см/с2

an=1,36 cм/c2

=7,53 см

Задача К2

Дано:

l1=0,4 м

l2=1,2 м

l3=1,4 м

l4=0,8 м

=60°

=60°

=60°

=90°

=120°

4=3с-2

=10с-2

Найти:

-?

2

O₁

4

O₂

Рис. К2.0.

Решение:

1) Строим положение данного механизма в соответствии с заданными узлами (рис К2.0)

2) Определяем скорость точки по формуле:

Точка одновременно принадлежит стержню . Зная и направление воспользуемся теоремой о проекциях скоростей двух точек тела (стержня ) на прямую, соединяющую эти точки (прямая )

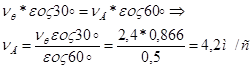
Точка В одновременно принадлежит к стержню 3 те к стержню АВ. При помощи теоремы о проекциях скоростей определяем скорость точки А:

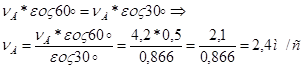
Для определения скорости точки D стержня АВ построим мгновенный центр скоростей для звенья АВ (рис. К 2.0)

Определяем угловую скорость звенья 3 по формуле:

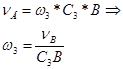
Из треугольника АС3В при помощи теоремы синусов определяем С3В:

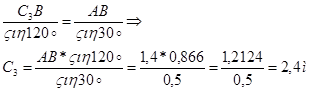
Т.О., угловая скорость стержня 3 равна:

Скорость точки D стержня АВ определяется по формуле:

С3D определяем при помощи теоремы синусов:

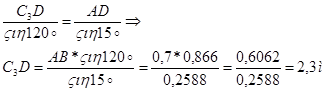
Итак: =

Определяем ускорение точки А.

Т.к., угловая ускорение известно, то

Найдем нормальное ускорение точки А определяем по формуле:

Ускорение точки А плоского механизма определяется по формуле:

Ответ:

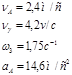
Задача Д1

Дано:

m=2 кг

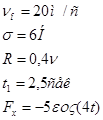
Найти:

x=f(t) – закон движения груза на участке ВС

А

CВ

D

x 30°

Рис. D 1.0.

Решение:

1) Рассмотрим движение груза D на участке АВ, считая груз материальной точкой.

Изображаем груз (в произвольном положении) и действующее на него силы:

. Проводим ось AZ в сторону движения и составляем дифференциальное уравнение движения груза в проекции на эту ось:

(1)

(2)

Далее, находим:

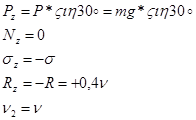(3)

Учитывая выражение (3) в (2) получим:

(4)

(5)

Принимая g=10ми/с2 получим:

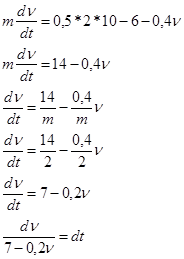
Интегрируем:

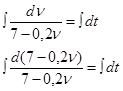
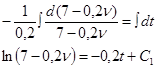
Начальные условия:

При t=0;

или

ln(7-0,2*)= C1

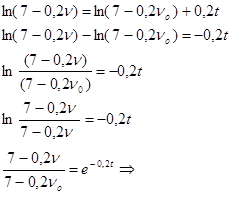
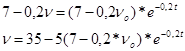
При t=t1=2,5сек, , получим:

2) Теперь рассмотрим движение груза на участке ВС, найденная скорость будет для движения на этом участке начальной скоростью

Изображаем груз (в произвольном положении) и действующие на него силы:

(рис. D1.0)

Проведем из точки В ось BX и составим дифференциальное уравнение движения груза в проекции на эту ось:

(6)

Т.к., то уравнение (6) примет вид:

(7)

Разделив обе части равенства на m=2 кг, получим

(8)

(9)

Умножим обе части уравнения (9) на и проинтегрируя, получим:

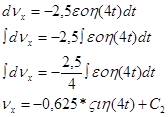
Учитывая начальные условия:

При

Т.о.,

Умножим обе части равенства на dt и снова интегрируем, получим:

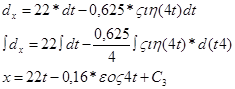
Начальные условия: при

Итак:

Ответ:

Это закон движения груза D в изогнутой трубе АВС.