Название: Расчет статически неопределимой рамы методом сил
Вид работы: реферат
Рубрика: Физика
Размер файла: 104.03 Kb
Скачать файл: referat.me-343663.docx
Краткое описание работы: Задача №5. Расчет статически неопределимой рамы методом сил Для статически неопределимой Е-образной рамы с одной скользящей и двумя неподвижными опорами используя метод сил, формулу Мора и правило Верещагина необходимо определить реакции опор и построить эпюры моментов, поперечных и продольных сил
Расчет статически неопределимой рамы методом сил
Задача №5.
Расчет статически неопределимой рамы методом сил
Для статически неопределимой Е-образной рамы с одной скользящей и двумя неподвижными опорами используя метод сил, формулу Мора и правило Верещагина необходимо определить реакции опор и построить эпюры моментов, поперечных и продольных сил
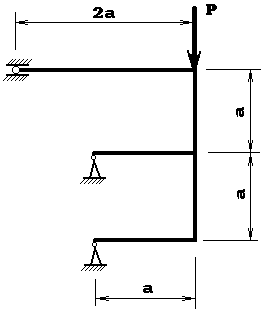
Построить эпюры M, Q и N.
Решение
Данная система дважды статически неопределима, так как рама прикреплена пятью связями, а уравнений статики для их определения – три. Выбираем основную систему путем отбрасывания лишних связей и заменой их неизвестными усилиями Х1 и Х2 . Фактически Х1 будет являться реакцией опоры С, а Х2 – вертикальной составляющей реакции опоры В.
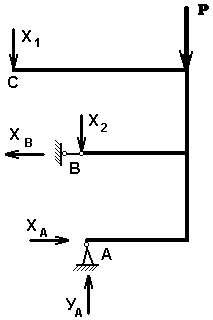
Составляем систему канонических уравнений метода сил:
![]() d11
×Х1
+ d12
×Х2
+ D1Р
= 0;
d11
×Х1
+ d12
×Х2
+ D1Р
= 0;
d21 ×Х1 + d22 ×Х2 + D2Р = 0.
Для определения коэффициентов при неизвестных и свободных членах необходимо построить эпюры изгибающих моментов поочередно для каждой силы.
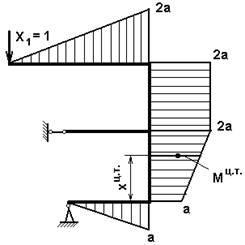
Эпюра единичных изгибающих моментов от единичной силы Х1
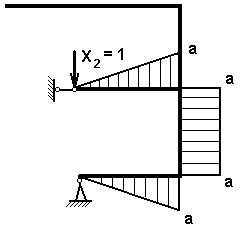
Эпюра единичных изгибающих моментов от единичной силы Х2
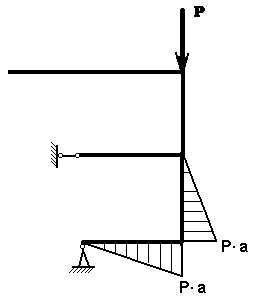
Грузовая эпюра от заданной нагрузки – силы Р.
Подсчитываем коэффициенты по формуле Мора используя правило Верещагина:
![]()
где ![]() – величина изгибающего момента единичной эпюры Хj
в точке, где расположен центр тяжести фигуры, образованной единичной эпюрой Хi
;
– величина изгибающего момента единичной эпюры Хj
в точке, где расположен центр тяжести фигуры, образованной единичной эпюрой Хi
;
![]() – площадь фигуры, образованной единичной эпюрой Хi
.
– площадь фигуры, образованной единичной эпюрой Хi
.
Например, для трапециевидного участка длиной L и размерами сторон м и М единичной эпюры Х1 находим координату центра тяжести для трапеции:
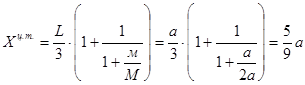 ;
;
Далее находим значение Мц.т. в этой точке для всех эпюр.
– для эпюры Х1 это будет:
![]() ,
,
– для эпюры Х2 в любой точке данного участка М равно а, следовательно:
![]()
– для эпюры Р это будет:
![]()
Соответственно площади эпюр на данном участке будут равны:
![]()
![]()
![]()
Аналогичным образом находим составляющие уравнения Мора для других, более простых участков и вычисляем требуемые коэффициенты:
![]()
![]()
![]()
![]()
![]()
Подставив найденные коэффициенты в систему канонических уравнений и сократив на ![]() и а3
получим систему двух уравнений с двумя неизвестными:
и а3
получим систему двух уравнений с двумя неизвестными:
![]()
![]()
![]() ×Х1
+
×Х1
+ ![]() ×Х2
+ Р = 0; 56×Х1
+ 11×Х2
+ 6Р = 0;
×Х2
+ Р = 0; 56×Х1
+ 11×Х2
+ 6Р = 0;
![]() ×Х1
+
×Х1
+ ![]() ×Х2
+
×Х2
+ ![]() ×Р = 0.11×Х1
+ 10×Х2
+ 7Р = 0;
×Р = 0.11×Х1
+ 10×Х2
+ 7Р = 0;
Вычитая из первого уравнения второе, получим более простое выражение, из которого выразим Х2 и подставим затем во второе уравнение;
45Х1 + Х2 – Р = 0;®Х2 = Р – 45Х1 ;
11 Х1 + 10Р – 450 Х1 + 5Р = 0;
Х1
= ![]() Р = 0,034Р;
Р = 0,034Р;
Х2
= Р – ![]() Р = –
Р = –![]() Р = –0,538Р;
Р = –0,538Р;
Найдя значения неизвестных усилий Х1 и Х2 , обратимся к основной системе и найдем ХА , УА и ХВ .
S У = 0;
УА – Х1 – Х2 – Р = 0;
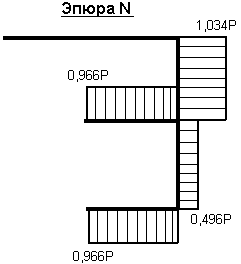
УА = Х1 + Х2 + Р = 0,034Р – 0,538Р + Р = 0,496Р;
S МА = 0;
Х1 ×а + ХВ ×а – Р×а = 0;
ХВ = Р – Х1 = 0,966Р;
S Х = 0;
ХА – ХВ = 0;
ХА = ХВ = 0,966Р;
Зная значения всех усилий, действующих на раму, строим эпюры М, Q и N:
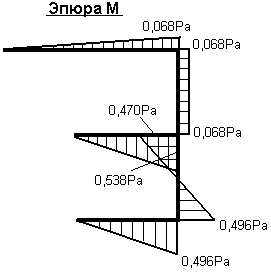
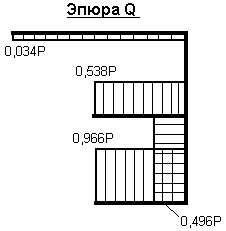
Похожие работы
-
Теоретическая механика. Статика
Требования к выполнению расчетно-графических работ. Примеры типовых задач: система сходящихся сил в плоскости; равновесие тела в плоскости; определение реакций двухопорной балки; равновесие системы тел в плоскости; равновесие пространственной системы сил.
-
Действие физических сил на конструкцию
Определение реакций опор составной конструкции по системе двух тел. Способы интегрирования дифференциальных уравнений. Определение реакций опор твердого тела. Применение теоремы об изменении кинетической энергии к изучению движения механической системы.
-
Расчет элементов статически неопределенных и статически определенных систем на прочность, жесткость
Введение Все твердые тела в той или иной степени воспринимают воздействие внешних сил без разрушения и существенного изменения геометрических размеров и формы, то есть обладают свойствами прочности и жесткости.
-
Электромеханические переходные процессы
Определение запаса статической устойчивости по пределу передаваемой мощности при передаче от генератора в систему мощности по заданной схеме электропередачи. Расчет статической и динамической устойчивости. Статическая устойчивость асинхронной нагрузки.
-
Расчет плоских ферм при подвижной нагрузке
Сургутский Государственный Педагогический Институт Кафедра высшей математики. Реферат "Методы расчета ферм при подвижной нагрузке" по дисциплине: Простейшие динамические модели
-
Сопромат
Задача № 1 Тема: Расчет на прочность статически определимых систем при растяжении и сжатии Требуется: 1. Построить эпюру продольного усилия Ni 2. По условию прочности подобрать размер поперечного сечение «а», если
-
Расчет вала при совместном действии изгиба и кручения по гипотезам прочности
Совместные действия изгиба и кручения, расчет с применением гипотез прочности. Значение эквивалентного момента по заданным координатам. Реакция опор в вертикальной и горизонтальной плоскости. Эпюра крутящихся, изгибающихся и вращающихся моментов.
-
Растяжение - сжатие
Построение эпюры нормальных сил и напряжений. Методика расчета задач на прочность. Подбор поперечного сечения стержня. Определение напряжения в любой точке поперечного сечения при растяжении и сжатии. Определение удлинения стержня по формуле Гука.
-
Техническая механика. Задачи
Қазақстан Республикасының білім және ғылым министрлігі Министерство образования и науки Республики Казахстан РИИ индустриалды-технологиялық колледжі
-
Прикладная механика
Задача 1 Для стального трубчатого вала , который оборачивается с постоянной угловой скоростью, требуется: Определить, пренебрегая трением в подшипниках, мощность на шкиве P0 .