Название: Автоматизированные формы

Вид работы: контрольная работа

Рубрика: Информатика и программирование

Размер файла: 56.33 Kb

Скачать файл: referat.me-133932.docx

Краткое описание работы: Структурная схема автоматизированной системы, передаточные функции каждого из звеньев и системы в целом, местной и общей обратной связи. Вычисление передаточной функции замкнутой и разомкнутой систем, координаты точек годографа по критерию Михайлова.

Автоматизированные формы

Федеральное Государственное образовательное учреждение

Высшего профессионального образования

«Омский государственный аграрный университет»

Кафедра электротехники и электрификации сельского хозяйства

Контрольная работа по предмету

«Автоматика»

Выполнил: Кеня А.А.

61 группа. Шифр 410

Проверил:

2009

Дано:

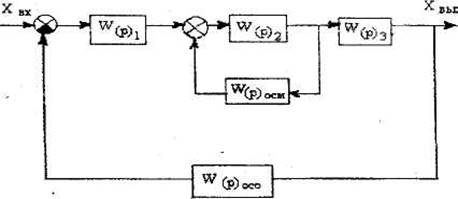
Рис. 1. Структурная схема AC: W (р) - передаточные функции звеньев

Уравнения звеньев в операторной форме имеют вид:

1-е звено:

2-е звено:

3-е звено:

4-е звено местной обратной связи (ОСМ):

5-е звено общей обратной связи (ОСО):

Таблица 1

Вариант	К1	К2	К3	Т1	Т2	Т3
0	1	1	2	1	4	2

Определить передаточные функции каждого звена и системы в целом. Определить устойчивость системы по критерию Михайлова.

По заданным уравнениям звеньев находим передаточные функции этих звеньев:

1.

2.

3.

4. Передаточная функция местной обратной связи:

5. Передаточная функция общей обратной связи:

Следует иметь в виду, что если передаточная функция звена обратной связи W(p)_осо =1,то это звено на структурной схеме можно не изображать, тогда структурная схема АС принимает вид.

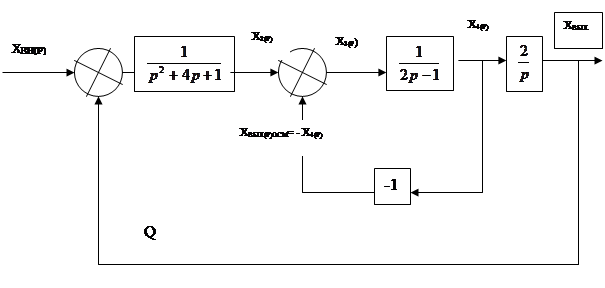
Рис. 2. Структурная схема АС

В этой задаче местная обратная связь положительная, поэтому сектор х_вых (р)осм не заштрихован. Передаточная функция для второго и четвертого звена вычисляется по формуле:

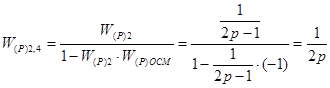
Находим общую передаточную функцию для разомкнутой АС, для чего имеющуюся замкнутую АС разомкнем в точке Q (этот разрыв можно сделать между любыми другими звеньями).

Общая передаточная функция всей системы для разомкнутого состояния будет равна:

Для замкнутой системы в случае единичной отрицательной обратной связи передаточная функция определяется по формуле:

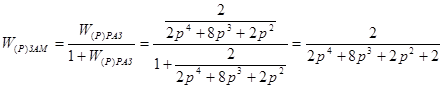
Вычисляем передаточную функцию замкнутой системы:

Для определения устойчивости АС по критерию Михайлова необходимо ωω иметь передаточную функцию АС для замкнутого состояния, а ее знаменатель является характеристическим многочленом.

В характеристическом многочлене для замкнутой АС вместо оператора р подставим значение iω и получим выражение вектора Михайлова:

M(ìω) = 2(ìω)⁴ + 8(ìω)³ + 2(ìω)² +2 = 2ω⁴ - 8 ìω³ -2ω² + 2 =

= 2(1 - ω² + ω⁴ ) +ì(-8ω)³

где R(ω) = 2 (1- ω² + ω⁴ ); I(ω)= - 8ω³ .

Найдем координаты точек годографа по критерию Михайлова так же, как при построении по критерию Найквиста.

При ω→ 0 получим

R(ω)_ω→0 → 2; I(ω)_ω→0 =0

При ω→ + ∞ получим

R(ω)_ω→∞ → + ∞; I(ω)_ω→∞ =-∞

Приравнивая I(ω) = 0, находим корни уравнения:

- 8ω³ = 0; ω = 0;

Приравнивая R(ω) = 0, находим корни уравнения:

2(ω⁴ - ω² + 1) = О,

2≠0

положив ω² = х, получим

х² -х+1=0

решаем уравнение:

Все корни получились мнимые, т.е. нет больше пересечений годографа с осью

ординат. Полученные данные заносятся в табл. 2.

Результаты вычислений

Таблица 2

ω	R(ω)	I(ω)	ω	R(ω)	I(ω)
0	2	0	1	2	-8
2	26	-64
∞	+∞	-∞

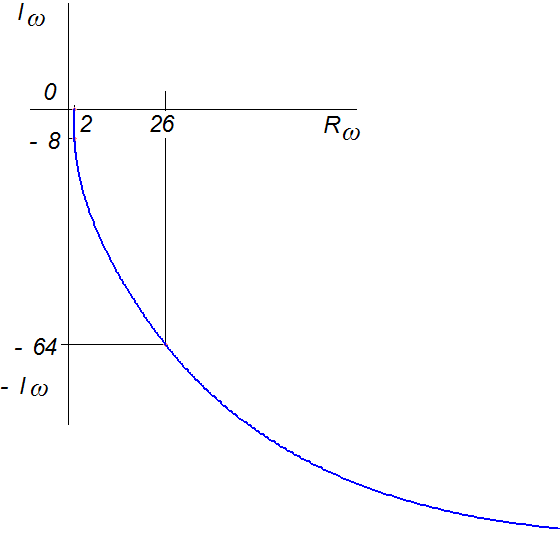
Рис. 3. Годограф по критерию Михайлова

Вывод: годограф по критерию Михайлова не пересекает последовательно оси координат, следовательно, автоматическая система неустойчива.