Название: Транспортные модели

Вид работы: лабораторная работа

Рубрика: Информатика и программирование

Размер файла: 164.08 Kb

Скачать файл: referat.me-136633.docx

Краткое описание работы: Оптимальное решение задач транспортного типа, математические модели; определение потребностей в грузах и суммарного объема поставок по пунктам назначения; сведение к минимуму общей суммы затрат на перевозку. Ситуации, ограничивающие транспортную задачу.

Транспортные модели

Лабораторная работа №4

Транспортные модели

Цель работы: научиться находить оптимальное решение задач транспортного типа.

Задание

Вариант 1. На четырех ткацких станках с объемом рабочего времени 200, 300, 250 и 400 станко-ч за 1 час можно изготовить соответственно 260, 200, 340 и 500 м ткани трех артикулов I, II, III. Составить оптимальную программу загрузки станков, если прибыль (в ден. ед.) от реализации 1 м ткани i-го артикула при ее изготовлении на j-м станке характеризуется элементами матрицы

,

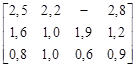а суммарная потребность в ткани каждого из артикулов равна 200, 100 и 150 тыс. м, учитывая, что ткань Iартикула не может производиться на третьем станке.

Табличная модель:

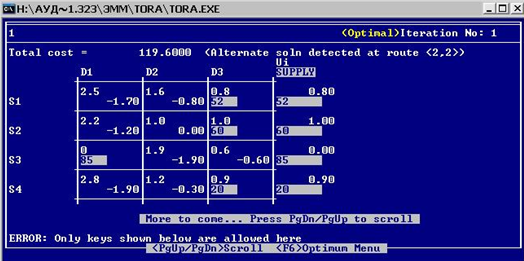
Контрольные вопросы:

1. Как записывается математическая модель задачи транспортного типа?

Обозначим через x_ij объем перевозок от i-го поставщика j-ому потребителю. Математическая модель задачи имеет вид:

1) объем поставок i-го поставщика должен равняться количеству имеющегося у него груза

;

2) объем поставок j-ому потребителю должен быть равен его спросу

;

3) объемы поставок должны выражаться неотрицательными числами

x_ij ³0; , ;

4) общая сумма затрат на перевозку груза должна быть минимальной

.

Если суммарный объем отправляемых грузов равен суммарному объему потребностей в этих грузах по пунктам назначения

,

то такая транспортная задача называется закрытой (сбалансированной), в противном случае — открытой (несбалансированной).

Если указанные затраты неизвестны (не указаны) соответствующие значения с_ij полагают равными нулю.

модель поставка потребность затрата

2. Как свести открытую транспортную задачу к закрытой?

Если имеет место открытая транспортная задача, ее необходимо свести к закрытой:

1) в случае перепроизводства – ввести фиктивного потребителя с необходимым объемом потребления (элементы матрицы с_ij , связывающие фиктивные пункты с реальными, имеют значения, равные затратам на хранение невывезенных грузов);

2) в случае дефицита – ввести фиктивного поставщика с недостающим объемом отправляемых грузов (элементы матрицы с_ij , связывающие фиктивные пункты с реальными, имеют значения, равные штрафам за недопоставку продукции).

3. Каковы основные ситуации, описывающие дополнительные ограничения транспортной задачи?

При решении практических задач зачастую приходится учитывать ряд дополнительных ограничений.

1. Отдельные поставки от определенных поставщиков некоторым потребителям должны быть исключены (из-за отсутствия необходимых условий хранения, чрезмерной перегрузки коммуникаций и т.д.). Это достигается искусственным значительным завышением затрат на перевозки с_ij в клетках, перевозки через которые следует запретить.

2. На предприятии необходимо определить минимальные суммарные затраты на производство и транспортировку продукции. С подобной задачей сталкиваются при решении вопросов, связанных с оптимальным размещением производственных объектов. Здесь может оказаться экономически более выгодным доставлять сырье из более отдаленных пунктов, но зато при меньшей его себестоимости. В таких задачах за критерий оптимальности принимают сумму затрат на производство и транспортировку продукции.

3. Ряд транспортных маршрутов, по которым необходимо доставить грузы, имеют ограничения по пропускной способности. Если, например, по маршруту A_i B_j можно провести не более qединиц груза, то B_j -й столбец матрицы разбивается на два столбца – и . В первом столбце спрос принимается равным , во втором – . Несмотря на то, что фактические затраты с_ij в обоих столбцах одинаковы и равны исходным, в столбце вместо истинного тарифа с_ij ставится искусственно завышенный тариф М (клетка блокируется). Затем задача решается обычным способом.

4. Поставки по определенным маршрутам обязательны и должны войти в оптимальный план независимо от того, выгодно это или нет. В этом случае уменьшают запас груза у поставщиков и спрос потребителей и решают задачу относительно тех поставок, которые необязательны. Полученное решение корректируют с учетом обязательных поставок.

5. Необходимо максимизировать целевую функцию задачи транспортного типа (например, задача об оптимальном распределении оборудования). В этом случае необходимо изменить знак в тарифах на противоположный. В ответе отрицательный знак игнорируется.

Вывод: я научилась находить оптимальное решение задач транспортного типа.