Название: Математическое программирование
Вид работы: контрольная работа
Рубрика: Информатика и программирование
Размер файла: 493.04 Kb
Скачать файл: referat.me-134591.docx
Краткое описание работы: Решение задачи линейного программирования симплекс-методом. Нахождение оптимального плана по критерию максимума прибыли. Транспорт - определение плана перевозок грузов на предприятие, которое обеспечивает минимальные совокупные транспортные издержки.
Математическое программирование
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ ФИНАНСОВ
ДОНЕЦКИЙ ФИЛИАЛ
Расчётная работа
по дисциплине “математическое программирование”
Вариант №10
Выполнил: ст. гр. МЭФ 2007-1п
Збыковский И.Е.
Проверила: Слепнёва Л.Д.
Донецк 2008 г.
1. Решение задачи линейного программирования симплекс-методом.
Задача 10.
Прибыль от изделий А,В,С составляет соответственно 13, 14, 15 единиц. Для их изготовления расходуется время работы двух станков, которые можно эксплуатировать 24 и 30 часов соответственно. В таблице – нормы времени на изделие.
| Станки | Изделия | ||
| А | В | С | |
| 1 | 5 | 4 | 5 |
| 2 | 6 | 3 | 3 |
Найти оптимальный план по критерию максимума прибыли.
Задачей является найти максимум функции прибыли
![]()
Где Xi – выпускаемые изделия i-го вида (А,В,С).
При существующих ограничениях ресурсов (время работы станков).
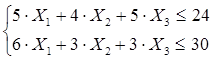
![]()
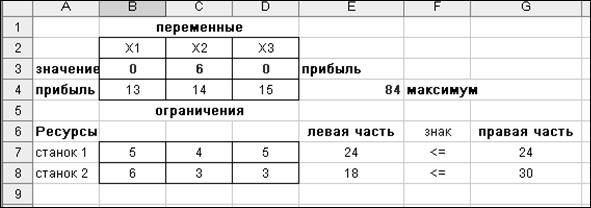
Исходя из решения оптимальный план выпуска – это выпуск изделия В в количестве 6 единиц. Этот план обусловит получение максимума прибыли в размере 84 единицы. При этом ресурс 1-го станка исчерпывается полностью, что говорит о дефицитности этого ресурса. Получить больше прибыли возможно только при увеличении этого ограничительного параметра. Второй же станок, при данном плане, будет простаивать 12 часов.
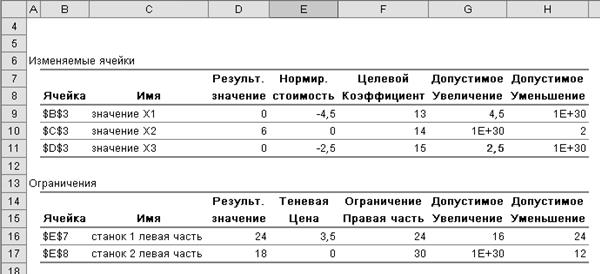
Исходя из отчёта по устойчивости решения, можно установить, что изготовление изделия С станет выгодным лишь в том случае, если увеличится его прибыльность на 2,5 единицы, т.е. составит 17,5 ед.
Пересчитаем план с новым условием:
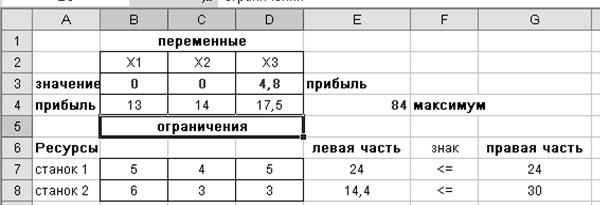
Отсюда видим, что план действительно изменился, и изготовление изделия С стало выгодным.
Дополнительное время использования 1 станка (опять же исходя из отчёта по устойчивости решения), не меняющее допустимость решения= +16 часов (общее время=40 часов), что позволит произвести + 4 дополнительных изделия и получить прибыль в размере 140 ед. (прирост = 16*3,5=56 ед.), при полном расходовании ресурсов обоих станков.

При принудительном изготовлении изделия А, исходя из значения нормированной стоимости из отчёта по устойчивости решения, прибыль уменьшится на 4,5 ед, т.е. составит 79,5
2. Решение транспортной задачи.
Задача 39.
Компания, занимающаяся добычей железной руды, имеет 4 карьера (С), производительность которых соответственно равна: 170, 150, 190 и 200 тыс.т. ежемесячно. Железная руда направляется на 3 принадлежащие этой компании обогатительный фабрики (S), мощности которых соответственно 250, 150, 270 тыс.т в месяц. Транспортные расходы (в тыс. руб.) на перевозку 1 тыс. руды с карьеров на фабрики:
| S1 | S2 | S3 | |
| C1 | 7 | 3 | 8 |
| C2 | 5 | 4 | 6 |
| C3 | 4 | 5 | 9 |
| C4 | 6 | 2 | 5 |
Задачей является определить план перевозок железной руды на обогатительные фабрики, который обеспечивает минимальные совокупные транспортные издержки.
Если обозначить С ij стоимость перевозки единицы груза из i-го карьера на j-ю обогатительную фабрику, а X ij – количество тонн груза, перевозимого из i-го карьера на j-ю обогатительную фабрику, то математически задача формулируется следующим образом:
![]()
Ограничения:
1. Суммарное количество перевозимой железной руды из каждого карьера не должно превышать возможности карьеров по добыче.
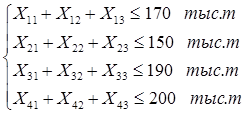
2. Суммарное количество пере перевозимой железной руды из каждого карьера не должно превышать возможности обогатительных фабрик по обогащению руды.
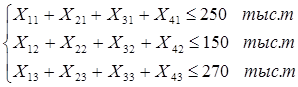
3. Неотрицательность количества перевозимой руды
![]()
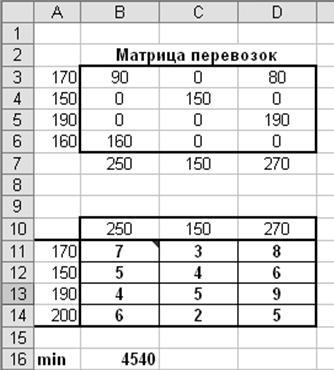
В результате был получен оптимальный план перевозок, который позволит удовлетворить потребности обогатительных фабрик в руде при минимальных суммарных затратах на перевозку = 4540 ден. ед.
Из плана видно, что мощности первых трёх карьеров используются полностью. Мощность по выработке 4-карьера недоиспользуется на 40 тыс. т.
Похожие работы
-
Методы решения задач линейного программирования с n-переменными
Характеристика основных методов линейного программирования с n- переменными, в частности, графического и симплекс-метода. Способы решения задачи по определению оптимальной структуры товарооборота, обеспечивающей торговому предприятию максимум прибыли.
-
Решение транспортной задачи методом потенциалов
Программа для решения транспортной задачи. Метод потенциалов, его математический смысл и порядок действий по его применению. Математические методы решения транспортных задач. Вычисление стоимости перевозок, расхода топлива, общей прибыли и окупаемости.
-
Постановка и решение транспортной параметрической задачи
Сущность и назначение основных алгоритмов оптимизации. Линейное программирование. Постановка и аналитический метод решения параметрической транспортной задачи, математическая модель. Метод решения задачи об оптимальных перевозках средствами MS Excel.
-
Метод потенциалов для решения транспортной задачи
Основные этапы решения транспортной задачи, использование метода потенциалов. Алгоритм решения методом аппроксимации Фогеля. Процедура построения цикла. Планирование перевозок из конечного числа пунктов отправления в конечное число пунктов назначения.
-
Транспортные модели
Оптимальное решение задач транспортного типа, математические модели; определение потребностей в грузах и суммарного объема поставок по пунктам назначения; сведение к минимуму общей суммы затрат на перевозку. Ситуации, ограничивающие транспортную задачу.
-
Регрессионные зависимости
Вычисление значений регрессионно-авторегрессионной зависимости заданного выражения линейного программирования. Графическое представление математической модели в виде уравнения регрессии. Принципи оптимизации производственных и коммерческих операций.
-
Графический метод решения задач линейного программирования
Расчет производства необходимого количества продукции для получения максимальной прибыли предприятия. Математическая модель для решения задач линейного программирования. Построение ограничений и целевых функций. Исследование чувствительности модели.
-
Решение задач исследования операций
Целевая функция. Базисная переменная. Симплекс метод, таблица. Коэффициенты при свободных переменных в целевой функции. Задача квадратичного программирования, максимизации функции. Функция Лагранжа. Координаты стационарной точки. Система ограничений.
-
Решение задачи оптимального управления
Математические основы оптимизации. Постановка задачи оптимизации. Методы оптимизации. Решение задачи классическим симплекс методом. Графический метод. Решение задач с помощью Excel. Коэффициенты целевой функции. Линейное программирование, метод, задачи.
-
Исследование операций
Математическая модель задачи. Система ограничений. Составление симплекс-таблиц. Разрешающий элемент. Линейное программирование. Коэффициенты при свободных членах. Целевая функция. Метод потенциалов, северо-западного угла. Выпуклость, вогнутость функции.