Referat.me
/ / Определение мольной теплоемкости методом интерполяции

Название: Определение мольной теплоемкости методом интерполяции

Вид работы: курсовая работа

Рубрика: Информатика и программирование

Размер файла: 119.4 Kb

Скачать файл: referat.me-136769.docx

Краткое описание работы: Написание программы решения технических задач языком высокого уровня Си: определение мольной теплоемкости кислорода методом интерполяции. Построение математических моделей, графиков и таблиц по результатам расчетов, составление текста программы.

Определение мольной теплоемкости методом интерполяции

Федеральное агентство по образованию

Федеральное государственное образовательное учреждение

Высшего профессионального образования

"СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ"

Институт космических и информационных технологий

Кафедра системы искусственного интеллекта

КУРСОВАЯ РАБОТА

Тема: ОПРЕДЕЛЕНИЕ МОЛЬНОЙ ТЕПЛОЕМКОСТИ МЕТОДОМ ИНТЕРПОЛЯЦИИ

Красноярск, 2009


Содержание

1. Цели и задачи курсовой работы

2. Теоретические основы курсовой работы

3. Массив исходных данных

4. Математические модели, применяемые для расчетов

5. Результаты расчетов, представляющиеся в виде таблиц и графиков

6. Текст программы

Вывод

Список литературы


1. Цели и задачи курсовой работы

Цель курсовой работы: закрепление навыков работы с языком высокого уровня Си, умение писать на этом языке программы решения технических задач (определение мольной теплоемкости кислорода, c помощью метода интерполяции).

Задача: определение приблизительных значений теплоемкости при температурах от 0 0 С до 1500 0 С с шагом Dt=10 0 C, методами интерполяции, позволяющими узнать приблизительные значения функции в промежуточных точках.

2. Теоретические основы курсовой работы

Результаты экспериментов зачастую представляют собой таблицу следующего вида:

X …
…

где Х - это может быть, например, время, а f(X) скорость или, как в нашем примере Х – это температура, а f(X) это теплоемкость.

Из этой таблицы, например, известны значения функции f(X) в точках х0 и х1 , но мы ничего не знаем о ее значении, например, в точке , однако, существуют методы, позволяющие узнать приблизительные значения функции в промежуточных точках. К таким методам относятся методы интерполяции.

Определение 1: Интерполяцией называется отыскание приближенной функции F(X), такой что F(xi )=f(xi ), где i=0,1…n, af(xi ) известные значения функции F(X) на отрезке[x0 , xn ]. Точки, в которых F(xi )=f(xi ) называются узлами интерполяции.

Определение 2: Если найденная интерполяционная функция F(X) для отрезка [x0 , xn ] имеет область определения вне этого отрезка, тогда она будет называться экстраполяцией функции f(x).

Одним из методов интерполяции является метод Интерполяции степенным многочленом

Будем искать интерполяционную функцию F(X) в виде многочлена степени n:

(*)

Многочлен Pn (x) имеет n+1 коэффициент, следовательно, n+1 условие, наложенное на многочлен однозначно определит его коэффициенты, которые могут быть получены их условия:

или

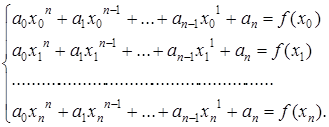
Разрешив эту систему относительно ai (i=0,1…,n), получим аналитическое выражение для полинома (*).


3. Массив исходных данных

Опытным путем найдены данные истинной мольной теплоемкости кислорода mср при постоянном давлении P=const, при температуре t=0 0 C, t=500 0 C, и t=1000 0 C, представленные таблицей 1.

Таблица 1.

№варианта
1 29.2741 33.5488 35.9144
2 29.2801 33.5501 35.9201
3 29.2729 33.5493 35.9167
4 29.30 33.5479 35.9251
5 29.2752 33.5485 35.9109
6 29.2748 33.5397 35.8999
7 29.2752 33.5501 35.9123
8 29.2744 33.5486 35.9128
9 29.2699 33.5484 35.9251
10 29.2742 33.5481 35.9109
11 29.2753 33.5399 35.9201
12 29.2748 33.5501 35.9167
13 29.2801 33.5493 35.9144
14 29.2729 33.5479 35.9201
15 29.2744 33.5485 35.9123
16 29.2699 33.5493 35.9128
17 29.2742 33.5479 35.9251
18 29.2753 33.5485 35.9109
19 29.2748 33.5397 35.9128
20 29.2752 33.5501 35.9251
21 29.2744 33.5486 35.9201
22 29.2741 33.5484 35.9167
23 29.2801 33.5481 35.9144
24 29.2753 33.5486 35.9201

мольный теплоемкость интерполяция программа

В нашем случае рассматриваются данные варианта №5.



№ варианта
5 29.2752 33.5485 35.9109

4. Математические модели, применяемые для расчетов

Интерполяционный многочлен mср =f(t0 ), будет иметь следующий вид:

,

на основе него составляется система линейных уравнений, разрешив которую относительно коэффициентов a, b, d, получим интерполяционную функцию. Составим для этих данных интерполяционные уравнения:

1.

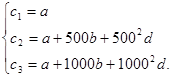
2.

3.

4.

5.

y=29,2752+0,0104575*t-0,0000038218*t2


5. Результатырасчетов

t°,C mср t°,C mср
0 29.2752 400 32.8467
10 29.3794 410 32.9203
20 29.4828 420 32.9932
30 29.5855 430 33.0653
40 29.6874 440 33.1366
50 29.7885 450 33.2072
60 29.8889 460 33.2770
70 29.9885 470 33.3460
80 30.0873 480 33.4143
90 30.1854 490 33.4818
100 30.2827 500 33.5485
110 30.3793 510 33.6145
120 30.4551 520 33.6797
130 30.5701 530 33.7441
140 30.6643 540 33.8078
150 30.7578 550 33.8707
160 30.8506 560 33.9329
170 30.9425 570 33.9943
180 31.0337 580 34.0549
190 31.1242 590 33.1148
200 31.2138 600 34.1739
210 31.3027 610 34.2322
220 31.3909 620 34.2897
230 31.4783 630 34.3466
240 31.5649 640 34.4026
250 31.6507 650 34.4579
260 31.7358 660 34.5124
270 31.8201 670 34.5661
280 31.9037 680 34.6191
290 31.9865 690 34.6713
300 32.0685 700 34.7228
310 32.1497 710 34.7735
320 32.2302 720 34.8234
330 32.3100 730 34.8725
340 32.3890 740 34.9209
t°,C mср t°,C mср
750 34.9686 1150 36.2470
760 35.0154 1160 36.2633
770 35.0615 1170 36.2788
780 35.1069 1180 36.2936
790 35.1514 1190 36.3076
800 35.1952 1200 36.3208
810 35.2383 1210 36.3333
820 35.2806 1220 36.3450
830 35.3221 1230 36.3559
840 35.3628 1240 36.3661
850 35.4028 1250 36.3755
860 35.4420 1260 36.3842
870 35.4805 1270 36.3920
880 35.5185 1280 36.3992
890 35.5551 1290 36.4055
900 35.5913 1300 36.4111
910 35.6267 1310 36.4159
920 35.6613 1320 36.4200
930 35.6952 1330 36.4233
940 35.7283 1340 36.4258
950 35.7607 1350 36.4276
960 35.7922 1360 36.4286
970 35.8230 1370 36.4288
980 35.8531 1380 36.4283
990 35.8824 1390 36.4270
1000 35.9109 1400 36.4250
1010 35.9387 1410 36.4222
1020 35.9656 1420 36.4186
1030 35.9919 1430 36.4142
1040 36.0173 1440 36.4091
1050 36.0420 1450 36.4032
1060 36.0660 1460 36.3966
1070 36.0891 1470 36.3892
1080 36.1116 1480 36.3810
1090 36.1332 1490 36.3721
1100 36.1541 1500 36.3624
1110 36.1742
1120 36.1935
1130 36.2121
1140 36.2299

График:

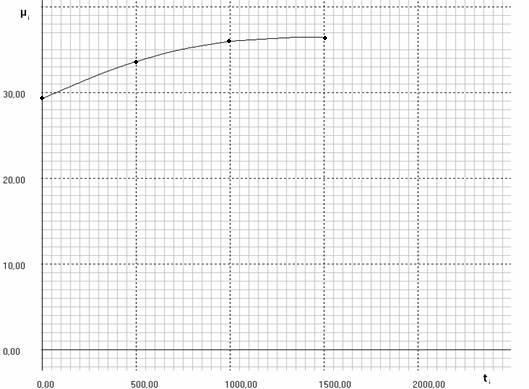
6. Текст программы

#include<stdio.h>

#include<conio.h>

#include<math.h>

float andrey (float c1, float c2, float m);

void main()

{clrscr();

float p1,p2,b,d;

int t1=500,i;

float k1=29.2752,k2=33.5485,k3=35.9109;

p1=(k2-k1)/t1;

p2=(k3-k1)/(2*t1);

d=-(p1-p2)/t1;

b=p1-t1*d;

printf ("n b=%f",b);

printf ("n d=%f",d);

andrey (b,d,k1);}

float andrey (float c1,float c2,float m)

{clrscr();

float t[1000];

float y[1000];

int h=10,i;

for (t[0]=0,i=0;i<=150;i++)

{t[i]=t[0]+i*h;

y[i]=m+c1*t[i]+c2*t[i]*t[i];

printf ("n t[%i]=%7.2f y[%i]=%7.2f",i,t[i],i,y[i]);}

getch();}


Вывод

Данные истинной мольной теплоемкости кислорода mср ,найденные опытным путем при постоянном давлении P=const, при температуре t=0 0 C, t=500 0 C, и t=1000 0 C, совпали с mср , найденные мной с помощью языка Си. Значит, метод интерполяции сработал.


Список литературы:

1. Паппас Крис Мюрей. Программирование на языке С++:-К.: Издательская группа BHV, 2000. - 320с.

2. Крячков А.В., Сухинина И.В., Томшин В.К. Программирование на С и С++. Практикум: Учеб. пособие для вузов/ Крячков А.В., Сухинина И.В., Томшин В.К.: Под ред. Томшина – 2-е изд. испр. – М.: Горячая линия – Телеком. 2000 – 344 с.: ил.

3. Подбельский В.В., Фомин С.С. Программирование на языке Си: Учеб. пособие – 2-е доп. изд. – М.: Финансы и статистика, 2000 – 600 с.: ил.

4. Гутер Р.С., Овчинский Б.В. Элементы численного анализа и математической обработки результатов опыта. – 2-е изд., перераб. – М.: Наука, 1970, 432 с.

5. Волков Е.А. Численные методы. – 2-е изд. испр. – М.: Наука, 1987, 248 с.

6. Мудров А.Е. Численные методы для ПЭВМ на языках Бейсик, Фортран и Паскаль – Томск: "РАСКО", 1991, - 272 с.: ил.

7. Плис А.И., Сливина Н.А. Лабораторный практикум по высшей математике.: Учеб. пособ. для втузов. . – 2-е изд., перераб. и доп. – М.: Высш. шк., 1994. – 416 с.

Похожие работы