Название: Моделирование линейных систем

Вид работы: контрольная работа

Рубрика: Информатика и программирование

Размер файла: 58.67 Kb

Скачать файл: referat.me-137011.docx

Краткое описание работы: Решение задачи на построение имитационной модели статической линейной системы, имеющей три входа и один выход. Предполагается, что на систему действуют случайные возмущения, результатом которых являются случайные составляющие с нормальным разделением.

Моделирование линейных систем

Министерство образования РФ

Тульский Институт Экономики и Информатики

Кафедра информационных технологий

Контрольная работа

По дисциплине «Теория систем и системный анализ»

По теме «Моделирование линейных систем»

Выполнил: студентка 1-го курса

Специальности ПИвЭ05

Андрианова К.Г.

Проверил:

Токарев В.Л.

Тула 2006

Введение

Целью системного анализа является моделирование системы.

Существуют два способа моделирование системы:

-аналитический;

-имитационный.

Аналитический способ применяется тогда, когда закономерности процессов, протекающих в системе, известны.

Имитационный способ применяется тогда, когда такие закономерности не известны, но в процессе функционирования системы, может быть накоплена выборка данных, содержащих информацию о поведении системы.

В контрольной работе решается задача построения имитационной модели статической линейной системы, имеющей три входа и один выход. Предполагается, что на систему действуют случайные возмущения, результатом которых являются случайные составляющие с нормальным разделением.

Построение математической модели системы

В контрольной работе решается задача построения имитационной модели статической решеткой системы, имеющей 3 входа и 1 выход.

Предполагается, что на систему действует случайное вращение, результатом которого является случайное составление с нормальным распределением.

Формирование матриц Х и Y по исходным данным (обучающая выборка – первые 20 строк матрицы):

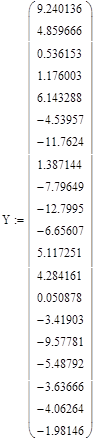
Найдем вектор исходных параметров:

1) Транспонируем матрицу Х.

2)

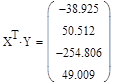
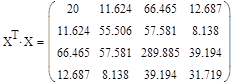
3)

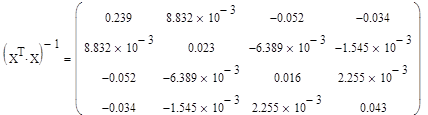
Получаем вектор исходных параметров:

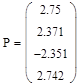
Сформируем матрицы X1 и Y1, полученные из контрольной выборки (следующие 20 чисел):

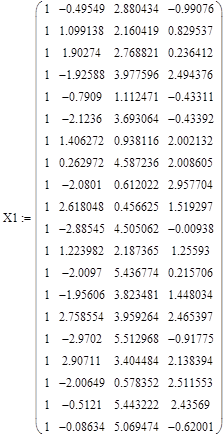
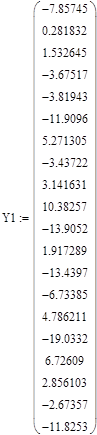
Для оценки случайности значений временного ряда ошибки необходимо сформировать матрицу Е по контрольной выборке.

Для того, чтобы сформировать матрицу Е нужно:

- найти скалярную величину У2(матрицу Х1 умножить на вектор случайных параметров Р)

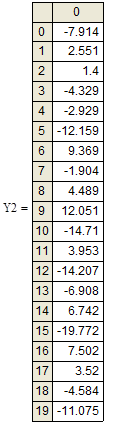
- найдем саму матрицу по формуле:

Получим:

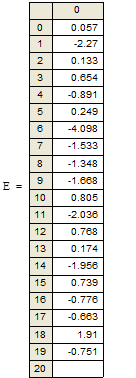
Сравним значения в матрице Е (значение сравнивается с предыдущим):

Длина серий получилась равно двум ().

Число серий получилось равное двенадцати().

По формуле должно быть: n > n1 и τ <τ1

Найдем n1 по формуле:

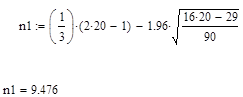
Найдем τ1 по формуле:

Получаем: 15 > 9.476 и 2 < 7.593

Следовательно: n > n1 и τ <τ1 – верно.

Гипотеза об адекватности не отвергается.

Для оценки взаимной зависимости значений ременного ряда, необходимо найти d. Чтобы его найти нужно выполнить следующие действия:

- сформировать матрицы Е1 и Е2

Для того, чтобы получить матрицу Е1 нужно скопировать значения из матрицы Е с 1 по 19; для получения матрицы Е2 мы скопируем значения из матрицы Е, начиная с 0 и заканчивая 18 значением, при этом получим:

Затем по формуле найдем матрицу Е3:

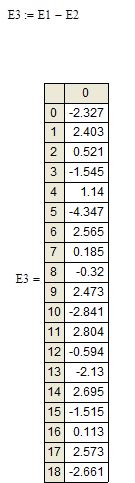
Теперь транспонируем Е3, получим:

Транспонируем матрицу Е, получим:

Затем по формулам находим d:

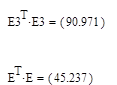
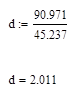
d=0..2, этом говорит о том, что имеется отрицательная взаимозависимость между ошибками. Гипотеза об адекватности модели не отвергается.

Проверка распределения случайной величины Е на нормальность заключается в оценке двух статистик: асимметрии и эксцесса.

Для того, чтобы найти асимметрию необходимо знать S, она является среднеквадратичной. Среднеквадратичная вычисляется по формуле:

Из этой формулы нам известно Е4.Для того, чтобы найти выполним следующие действия:

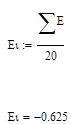
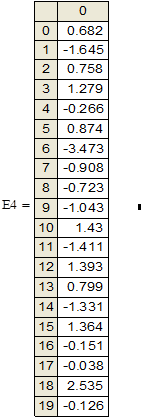
Теперь транспонируем полученную матрицу Е4, получим:

Теперь мы можем найти S:

Мы нашли S, теперь можем найти асимметрию (А), подставив Е4 в формулу:

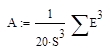
Далее находим эксцесс по формуле, подставляя S. Эксцесс обозначим буквой В.

Получим:

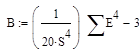
Чем ближе эксцесс к 0, то считается это нормально.

Если выполняется следующее условие

То гипотеза об адекватности не отвергается. Следовательно, гипотеза, об адекватности модели отвергается.

Заключение

В контрольной работе решалась задача построения имитационной модели статической системы, имеющей 3 входа и 1 выход.

Предполагалось, что на систему действует случайное возмещение, результатом которого является случайное составление с нормальным распределением.

В контрольной работе производилась проверка адекватности модели системы. Проверка состояла из трёх этапов:

1. Оценки случайности значений временного ряда ошибки (здесь были выполнены оба неравенства n > n1 и τ <τ1 – это означает, что гипотеза об адекватности не отвергается).

2. Оценка взаимной зависимости значений временного ряда (d=0..2(2.011) - -это означает, что имеется отрицательная взаимозависимость между ошибками).

3. Проверка распределения случайной величины на нормальность (условие, при котором гипотеза об адекватности не отвергается, не выполняется).