Название: Моделирование структурных схем в среде SIMULINK пакета MATLAB

Вид работы: лабораторная работа

Рубрика: Информатика и программирование

Размер файла: 54.35 Kb

Скачать файл: referat.me-137022.docx

Краткое описание работы: Практические навыки моделирования структурных схем в среде SIMULINK пакета MATLAB. Построение графиков функций в декартовой системе координат. Решение систем линейных и нелинейных уравнений. Работа с блоками Sum, Algebraic Constraint, Gain, Product.

Моделирование структурных схем в среде SIMULINK пакета MATLAB

Целью данной лабораторной работы является изучение принципов и получения практических навыков моделирования структурных схем в среде SIMULINK пакета MATLAB.

ТЕОРЕТИЧЕСКИЕ ИССЛЕДОВАНИЯ

Задание 1

Построить график функции в декартовой системе координат. Результаты представить в виде графика.

Диапазон изменения аргумента: 0.1-1.8

Шаг: 1/20=0.05

Структурная схема для построения данного графика функции представлена на рисунке 1.1

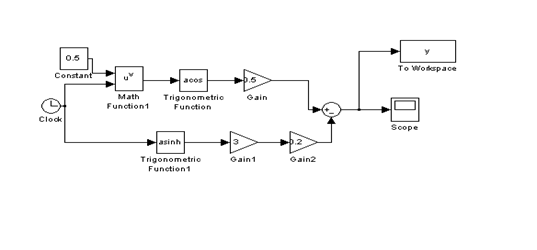
Рисунок 1.1 – Структурная схема моделирования функции к заданию 1

Задание 2

Решить системы линейных и нелинейных уравнений. Начальные приближения:

;

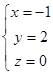Задана система линейных уравнений:

;

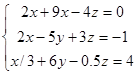Преобразую систему к виду:

;

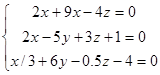Структурная схема для решения данного линейногоуравнения представлена на рисунке 1.2

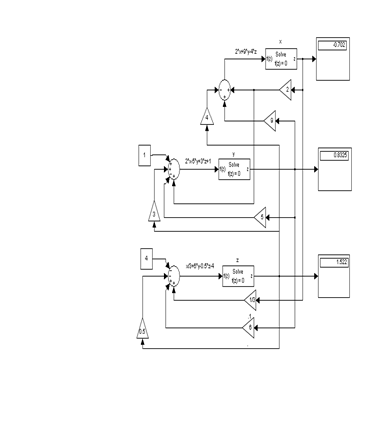
Рисунок 1.2 - Структурная схема для решения системы линейныхуравненийк заданию 2

Задана система нелинейных уравнений:

;

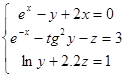Преобразую систему к виду:

;

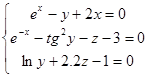Структурная схема решения данного линейногоуравнения представлена на рисунке 1.3

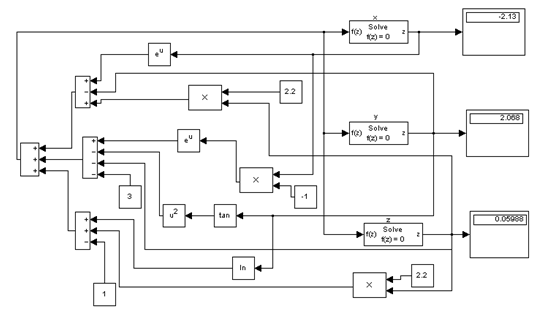
Рисунок 1.3 - Структурная схема для решения системы нелинейныхуравненийк заданию 2

Задание 3

Осуществить моделирование структуры, представленной на рисунке 1.4

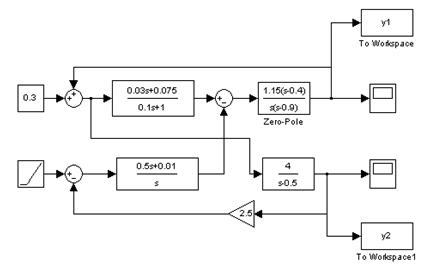
Рисунок 1.4 – Структурная схема к заданию 3

ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ

1. Структурная схема для построения графика функции 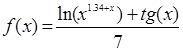к заданию 1 представлена на рисунке 2.1

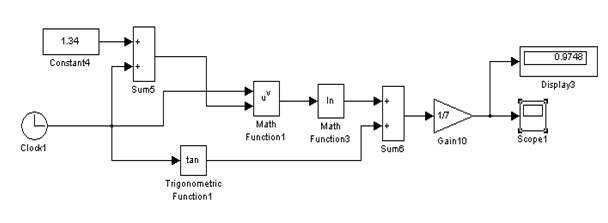
Рисунок 2.1 – Структурная схема моделирования функции к заданию 1

Построил график функции к заданию 1, представленный на рисунке 2.2.

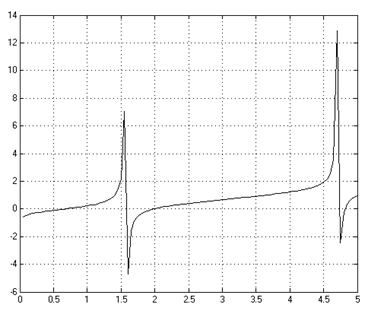
Рисунок 2.2 – График функции к заданию 1

2. Задана система линейных уравнений:

;

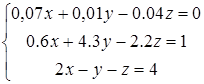Структурная схема для решения данного линейногоуравнения представлена на рисунке 2.3

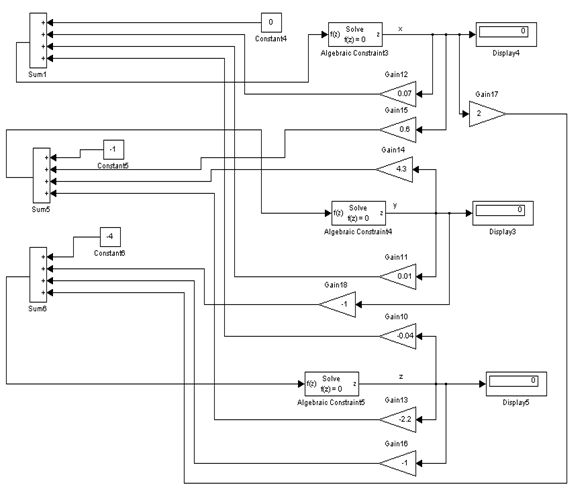Рисунок 2.3 - Структурная схема для решения системы линейныхуравненийк заданию 2

Построил структурные модели к заданию 2. Для линейной системы уравнений получил следующие значения:

;

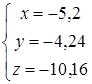3. Задана система нелинейных уравнений:

;

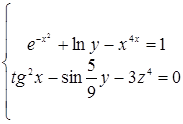Структурная схема решения данного линейногоуравнения представлена на рисунке 2.4

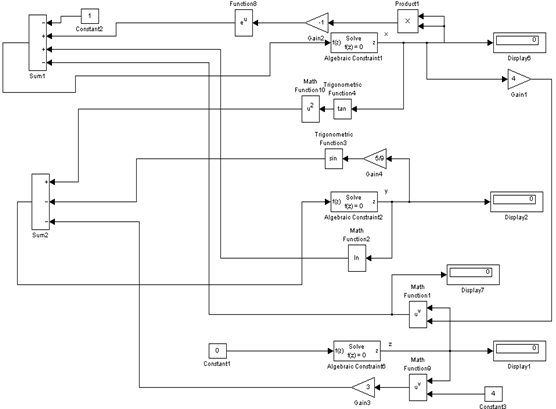
Структурная схема для решения системы нелинейныхуравненийк заданию 2.

Для нелинейной системы уравнений получил такие значения:

.

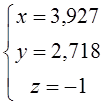4. Построил структурную модель к заданию 3 (рисунок 2.5). График результатов работы модели F ( t , y 1 ) представлен на рисунке 2.6.

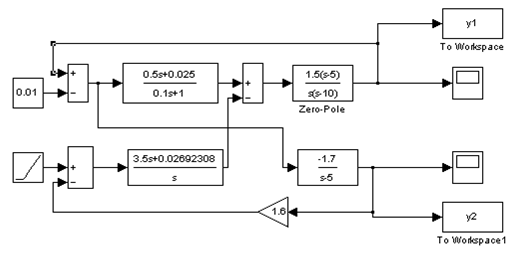
Рисунок 2.5 – Структурная схема к заданию 3

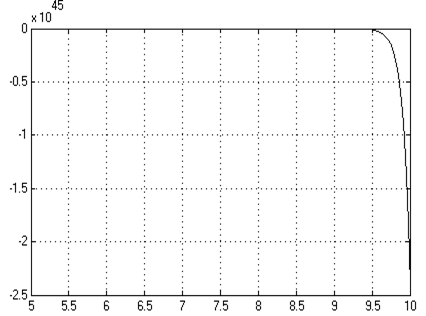
Рисунок 2.6 - График F ( t , y 1 ) результатов работы функции модели 3 к заданию 3

График результатов работы модели F ( t , y 2 ) представлен на рисунке 2.7.

y

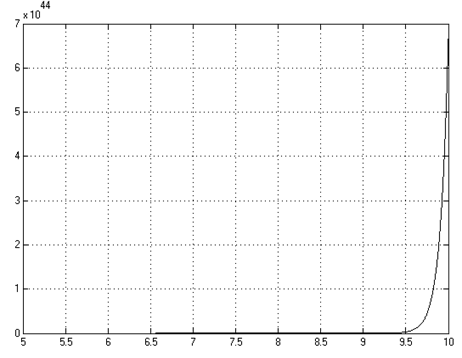
Рисунок 2.7 - График F ( t , y 2 ) результатов работы функции модели 3 к заданию 3

ВЫВОДЫ

В результате выполнения данной лабораторной работы получил практические навыки моделирования структурных схем в среде SIMULINK пакета MATLAB. Также я научился строить графики функций в декартовой системе координат (рисунок 2.1). Я научился решать системы линейных и нелинейных уравнений, то есть нашел корни этих уравнений

А также получил результаты работы модели в задании 3 (рисунок 2.2 и 2.3).

Научился работать с такими блоками, как Sum, AlgebraicConstraint, Gain, Productи другими.