Referat.me / Информатика и программирование / Создание программы табуляции функций

Название: Создание программы табуляции функций

Вид работы: курсовая работа

Рубрика: Информатика и программирование

Размер файла: 165.8 Kb

Скачать файл: referat.me-137090.docx

Краткое описание работы: Определение функции, ее графика и множества. Проблема повышения качества вычислений, как несоответствие между желаемым и действительным. Совершенствование методов организации информационных процессов. Создание программной реализации табуляции функций.

Создание программы табуляции функций

Содержание

Введение

1 Теоретическая часть

2 Программная реализация решения задачи

3 Пример выполнения программы

Заключение

Список использованных источников и литературы

Введение

В XXI веке в развитии человеческой цивилизации происходят глобальные изменения, ведущие к её новому этапу - постиндустриальному обществу, все шире использующему компьютеризированные орудия труда и информационные технологии.

Стремительное развитие индустрии, влечет за собой все больший и больший интерес начинающих программистов создавать то, что актуально в наше время. Мы в своей курсовой работе предлагаем упрощенный и автоматизированный вариант табуляции функций.

Данная программа, написанная на языке высокого уровня C++ в среде визуального программирования CodeGearRadStudio 2009.

Цель написания данной курсовой работы – табуляция функций.

Курсовая работа проста, удобна и практична в использовании.

Курсовая работа содержит: введение, теоретическую часть, практическую реализацию, заключение, литературу, которая использовалась при написании курсовой работы.

1. Теоретическая часть

Понятие функции.

Пусть Х и Y - некоторые множества.

Если каждому элементу xХ ставится в соответствие по некоторому правилу единственный элемент yY , то говорят, что на множестве Х задана функция (отображение) со значениями в множестве Y :

f : XY, y=f(x).

Множество Х называется областью определения функции и обозначается Dom(f) или D(f), множество Y называется множеством значений функции и обозначается Im(f) или I(f).

Если функция fпереводит элемент xХ в элемент yY, т.е. y=f(x), то у называют образом элемента х, а х называют прообразом элемента у. Образ всегда единственен.

Если обратное соответствие, переводящее У в Х является функцией, т.е. у каждого элемента yУ имеется единственный прообраз xХ, то это соответствие называют обратным отображением, или обратной функцией.

f^-1 : YХ, х=f^-1 (у).

Обратная функция обратима, и обратная функция к обратной функции совпадает с исходной функцией (f^-1 )^-1 = f .

Графиком числовой функции y=f(x) называется совокупность точек плоскости вида (x , f(x)), где хD(f).

Табуляция функции означает создать таблицу, в которой для каждого значения аргумента вычислено соответствующее значение функции.

2. Программная реализация решения задачи

Файл UTabulation.h

//---------------------------------------------------------------------------

#ifndef UTabulationH

#define UTabulationH

//---------------------------------------------------------------------------

#include <Classes.hpp>

#include <Controls.hpp>

#include <StdCtrls.hpp>

#include <Forms.hpp>

#include "HandTuning.h"

#include "Chart.hpp"

#include "Series.hpp"

#include "TeEngine.hpp"

#include "TeeProcs.hpp"

#include <ExtCtrls.hpp>

#include "HandTuning.h"

#include <Grids.hpp>

//---------------------------------------------------------------------------

class TfrmTabulation : public TForm

{__published: // IDE-managed Components

THandTuning *htMin;

THandTuning *htMax;

THandTuning *htStep;

TLabel *Label1;

TLabel *Label2;

TLabel *Label3;

TChart *chGraph;

TFastLineSeries *Series1;

TButton *btnCalc;

TButton *btnExit;

TButton *btnClear;

TStringGrid *sgrXY;

TRadioGroup *rgrFunction;

void __fastcall btnExitClick(TObject *Sender);

void __fastcall btnCalcClick(TObject *Sender);

void __fastcall btnClearClick(TObject *Sender);

private: // User declarations

double __fastcall function1(double x);

double __fastcall function2(double x);

double __fastcall function3(double x);

double __fastcall function4(double x);

double __fastcall function5(double x);

double __fastcall function6(double x);

public:// User declarations

__fastcall TfrmTabulation(TComponent* Owner);};

//---------------------------------------------------------------------------

extern PACKAGE TfrmTabulation *frmTabulation;

//---------------------------------------------------------------------------

#endif

ФайлUTabulation.cpp

//---------------------------------------------------------------------------

#include <vcl.h>

#pragma hdrstop

#include "UTabulation.h"

//---------------------------------------------------------------------------

#pragma package(smart_init)

#pragma link "Chart"

#pragma link "HandTuning"

#pragma link "Series"

#pragma link "TeEngine"

#pragma link "TeeProcs"

#pragma link "HandTuning"

#pragma resource "*.dfm"

TfrmTabulation *frmTabulation;

double __fastcall TfrmTabulation::function1(double x)

{return sin(x);}

//---------------------------------------------------------------------------

double __fastcall TfrmTabulation::function2(double x)

{return tan(3 * x);}

//---------------------------------------------------------------------------

double __fastcall TfrmTabulation::function3(double x)

{return cos(2 * x);}

//---------------------------------------------------------------------------

double __fastcall TfrmTabulation::function4(double x)

{return (4 - x) / 2;}

//----------------------------------------------------------

double __fastcall TfrmTabulation::function5(double x)

{return (1 - tan(x)) / (1 + tan(x));}

//----------------------------------------------------------

double __fastcall TfrmTabulation::function6(double x)

{return cos(x) + sin(x);}

//----------------------------------------------------------__fastcall TfrmTabulation::TfrmTabulation(TComponent* Owner)

: TForm(Owner)

{sgrXY->Rows[0]->Strings[0] = "y";

sgrXY->Rows[0]->Strings[1] = "x";}

//----------------------------------------------------------

void __fastcall TfrmTabulation::btnExitClick(TObject *Sender)

{this->Close();}

//----------------------------------------------------------

void __fastcall TfrmTabulation::btnCalcClick(TObject *Sender)

{Series1->Clear();

sgrXY->Cells[0][1] = "";

sgrXY->Cells[1][1] = "";

sgrXY->RowCount = 2;

for(double i = htMin->Value, j=0; i < htMax->Value; i = i + htStep->Value, j++)

{sgrXY->RowCount++;

sgrXY->Rows[j+1]->Strings[0] = FormatFloat("0.00", i);

switch(rgrFunction->ItemIndex)

{case 0:

sgrXY->Rows[j+1]->Strings[1] = FormatFloat("0.00", function1(i));

Series1->AddXY(i, function1(i), "",clRed) ;

break;

case 1:

sgrXY->Rows[j+1]->Strings[1] = FormatFloat("0.00", function2(i));

Series1->AddXY(i, function2(i), "",clRed) ;

break;

case 2:

sgrXY->Rows[j+1]->Strings[1] = FormatFloat("0.00", function3(i));

Series1->AddXY(i, function3(i), "",clRed) ;

break;

case 3:

sgrXY->Rows[j+1]->Strings[1] = FormatFloat("0.00", function4(i));

Series1->AddXY(i, function4(i), "",clRed) ;

break;

case 4:

sgrXY->Rows[j+1]->Strings[1] = FormatFloat("0.00", function5(i));

Series1->AddXY(i, function5(i), "",clRed) ;

break;

case 5:

sgrXY->Rows[j+1]->Strings[1] = FormatFloat("0.00", function6(i));

Series1->AddXY(i, function6(i), "",clRed) ;

break;}}

sgrXY->RowCount = sgrXY->RowCount >= 2 ? sgrXY->RowCount : sgrXY->RowCount--;}

//----------------------------------------------------------

void __fastcall TfrmTabulation::btnClearClick(TObject *Sender)

{Series1->Clear();

sgrXY->Cells[0][1] = "";

sgrXY->Cells[1][1] = "";

sgrXY->RowCount = 2;

htMin->Value = 0;

htMax->Value = 0;

htStep->Value = 0.1;}

//---------------------------------------------------------------------------

3. Пример выполнения программы

Пример 1.

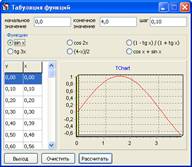
Рисунок 1 – Табуляция функции

Пример 2.

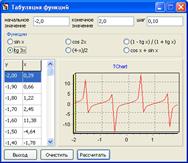
Рисунок 2 – Табуляция функции

Пример 3.

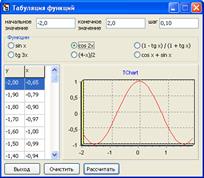
Рисунок 3 – Табуляция функции

Пример 4.

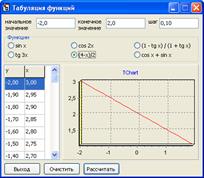
Рисунок 4 – Табуляция функции

Пример 5.

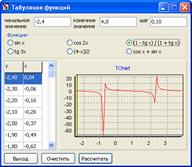
Рисунок 5 – Табуляция функции

Пример 6.

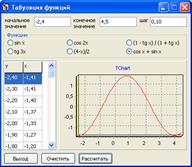
Рисунок 6 – Табуляция функции

Пример 7.

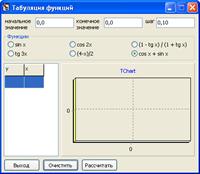
Рисунок 7 – Очистка

Заключение

Проблема повышения качества вычислений, как несоответствие между желаемым и действительным, существует и будет существовать в дальнейшем. Ее решению будет содействовать развитие информационных технологий, которое заключается как в совершенствовании методов организации информационных процессов, так и их реализации с помощью конкретных инструментов – сред и языков программирования.

Итогом работы можно считать созданную программу табуляции функций. Созданная программная реализация может служить органической частью решения более сложных задач.

Список использованных источников и литературы

1. Архангельский, А.Я. Программирование в С++ Builder 6. [Текст] / А.Я.Архангельский. – М.: Бином, 2003. С. 1154.

2. Ахо, А.. Построение и анализ вычислительных алгоритмов [Электронный ресурс] / А. Ахо, Дж. Хопкрофт, Дж.. Ульман. – М.: Мир. 1999. С. 143.

3. Бронштейн, И.Н. Справочник по математике для инженеров и учащихся втузов [Текст] / И.Н. Бронштейн, К.А. Семендяев. – М.: Наука, 2007. – 708 с.

4. Кремер, Н.Ш. Высшая математика для экономистов: учебник для студентов вузов. [Текст] / Н.Ш.Кремер, 3-е издание – М.:ЮНИТИ-ДАНА, 2006. C. 412.

5. Калиткин, Н.Н. Численные методы. [Электронный ресурс] / Н.Н. Калиткин. – М.: Питер, 2001. С. 504.

6. Павловская, Т.А. Программирование на языке высокого уровня. [Текст] / Т.А. Павловская. – М.: Питер, 2003. С. 461.

7. Семакин, И.Г. Основы программирования. [Текст] / И.Г.Семакин, А.П.Шестаков. – М.: Мир, 2006. C. 346.

8. Табуляция функций [Электронный ресурс] – Режим доступа: http://programmer.zp.ua/index.php

Создание программы табуляции функций

Похожие работы