Название: Метод касательных (метод Ньютона)
Вид работы: реферат
Рубрика: Информатика и программирование
Размер файла: 50.58 Kb
Скачать файл: referat.me-138308.docx
Краткое описание работы: Содержание Содержание 1 Используемая литература 1 Метод Ньютона (касательных). 2 Описание 2 Блок-схема алгоритма 3 Листинг программы 4 Результаты работы программы 6
Метод касательных (метод Ньютона)
Содержание
Содержание. 1
Используемая литература. 1
Метод Ньютона (касательных). 2
Описание. 2
Блок-схема алгоритма. 3
Листинг программы.. 4
Результаты работы программы.. 6
Пример №1. 6
Пример №2. 6
Пример №3. 7
Метод итераций. 8
Блок-схема алгоритма. 8
Листинг программы.. 9
Результаты работы программы.. 11
Пример №1. 11
Пример №2. 11
Пример №3. 12
Используемая литература
1. http://www.kyshtym.net.ru/rww/ Учимся программировать на С++
2. http://www.sprin.ru/soft.php Решение линейных уравнений методом Ньютона (касательных)
Метод Ньютона (касательных).
Описание
В рамках метода Ньютона предполагается, что функция дифференцируема. Согласно этому методу строится линейная аппроксимация функции в начальной точке, а точка, в которой аппроксимирующая линейная функция обращается в нуль, принимается в качестве следующего приближения.
Итерационый процесс схождения к корню реализуется формулой:
xn+1
=xn
-f(xn
)/f '(xn
). Вычисления продолжаются пока соблюдается условие
|xn+1
-xn
|>=eps.
В зависимости от выбора начальной точки и вида функции алгоритм по методу Ньютона может как сходиться к корню уравнения, так и расходиться.
Ниже приведена блок-схема алгоритма и листинг программы, реализующей данный алгоритм на языке С++. Также привожу текст, которая выдает данная программа при решении исходного уравнения.
Блок-схема алгоритма
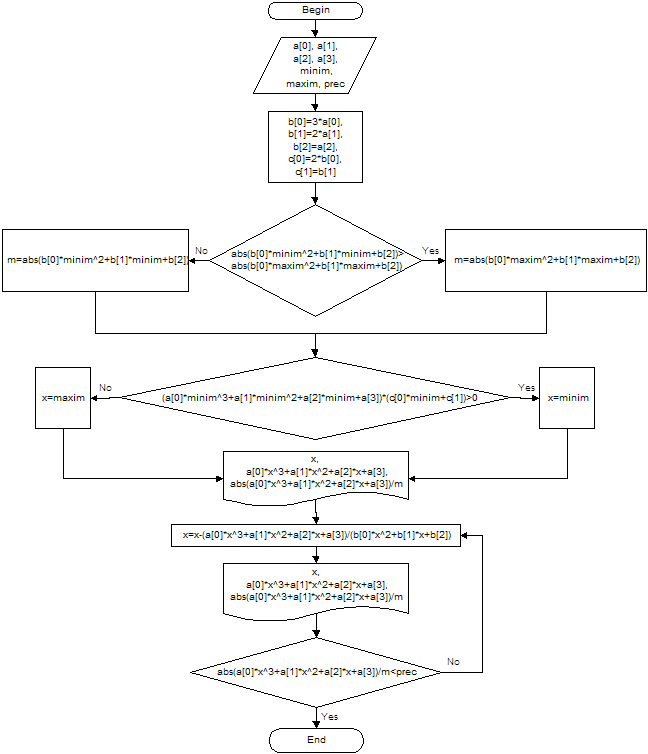
Листинг программы
//метод Ньютона для решения кубических уравнений
#include<math.h>
#include<iostream.h>
double a[4]={0},
b[3]={0},
c[2]={0},
prec=0.00000;
double minim=0, maxim=0;
void Hello(void);
void Input();
void Derivative();
void Calculation();
double Calc_Fun(double);
double Calc_First(double);
double Calc_Second(double);
main(void)
{
Hello();
Input();
Derivative();
Calculation();
return 0;
}
void Hello(void)
{
cout<<"Программа для решения кубических уравнений методом касательных (метод Ньютона).nn";
}
void Input()
{
cout<<"Кубическое уравнение имеет вид"<<endl
<<"a1*x^3+a2*x^2+a3*x+a4=0"<<endl<<endl;
for (int i=0;i<4;i++)
{
cout<<"Введите значение коэффициента a["<<i+1<<"] : ";
cin>>a[i];
}
cout<<endl<<"Необходимо указать интервал поиска решения."<<endl
<<"Введите нижнюю границу поиска : ";
cin>>minim;
cout<<"Введите верхнюю границу поиска : ";
cin>>maxim;
while(minim==maxim||minim>maxim)
{
cout<<"nНижняя граница должна быть меньше верхней и не может быть ей равна."<<endl
<<"Повторите ввод нижней границы : ";
cin>>minim;
cout<<"Повторите ввод верхней границы : ";
cin>>maxim;
}
cout<<"Введите допустимую погрешность : ";
cin>>prec;
}
void Derivative()
{
b[0]=a[0]*3;
b[1]=a[1]*2;
b[2]=a[2];
c[0]=b[0]*2;
c[1]=b[1];
cout<<"nnn"
<<"Исходное уравнение имеет вид : nn"
<<a[0]<<"x^3+("<<a[1]<<")x^2+("<<a[2]<<")x+("<<a[3]<<")=0nn"
<<"Первая производная имеет вид : nn"
<<"f'(x)="<<b[0]<<"x^2+("<<b[1]<<")x+("<<b[2]<<")nn"
<<"Вторая производная имеет вид : nn"
<<"f''(x)="<<c[0]<<"x+("<<c[1]<<")nn";
}
void Calculation()
{
double x=0, m=0;
cout<<"-------------------------------------------------"<<endl
<<"| Xn | f(Xn) | |f(Xn)|/m |"<<endl
<<"-------------------------------------------------"<<endl;
if (abs(Calc_Fun(minim))*abs(Calc_Second(minim))>0) x=minim;
else x=maxim;
if (Calc_First(minim)>Calc_First(maxim)) m=abs(Calc_First(maxim));
else m=abs(Calc_First(minim));
cout<<"|";
cout.width(15);cout.precision(10);
cout<<x;
cout<<"|";
cout.width(15);cout.precision(10);
cout<<Calc_Fun(x);
cout<<"|";
cout.width(15);cout.precision(10);
cout<<(fabs(Calc_Fun(x))/m);
cout<<"|n";
while((fabs(Calc_Fun(x))/m)>prec)
{
x=(x-(Calc_Fun(x)/Calc_First(x)));
cout<<"|";
cout.width(15);cout.precision(10);
cout<<x;
cout<<"|";
cout.width(15);cout.precision(10);
cout<<Calc_Fun(x);
cout<<"|";
cout.width(15);cout.precision(10);
cout<<fabs(Calc_Fun(x))/m;
cout<<"|n";
}
cout<<"-------------------------------------------------";
}
double Calc_Fun(double x)
{
return (a[0]*x*x*x+a[1]*x*x+a[2]*x+a[3]);
}
double Calc_First(double x)
{
return (b[0]*x*x+b[1]*x+b[2]);
}
double Calc_Second(double x)
{
return (c[0]*x+c[1]);
}
Результаты работы программы
Пример №1
![]()
Программа для решения кубических уравнений методом касательных (метод Ньютона).
Кубическое уравнение имеет вид
a1*x^3+a2*x^2+a3*x+a4=0
Введите значение коэффициента a[1] : 1
Введите значение коэффициента a[2] : -6
Введите значение коэффициента a[3] : -9
Введите значение коэффициента a[4] : 58
Необходимо указать интервал поиска решения.
Введите нижнюю границу поиска : -4
Введите верхнюю границу поиска : -3
Введите допустимую погрешность : 0.00005
Исходное уравнение имеет вид :
1x^3+(-6)x^2+(-9)x+(58)=0
Первая производная имеет вид :
f'(x)=3x^2+(-12)x+(-9)
Вторая производная имеет вид :
f''(x)=6x+(-12)
-------------------------------------------------
| Xn | f(Xn) | |f(Xn)|/m |
-------------------------------------------------
| -4| -66| 1.222222222|
| -3.24137931| -9.922506048| 0.183750112|
| -3.079817529| -0.40621762| 0.007522548518|
| -3.07261683|-0.000789793230|1.462580056e-05|
-------------------------------------------------
Пример №2
![]()
Программа для решения кубических уравнений методом касательных (метод Ньютона).
Кубическое уравнение имеет вид
a1*x^3+a2*x^2+a3*x+a4=0
Введите значение коэффициента a[1] : 1
Введите значение коэффициента a[2] : -6
Введите значение коэффициента a[3] : -9
Введите значение коэффициента a[4] : 58
Необходимо указать интервал поиска решения.
Введите нижнюю границу поиска : 3
Введите верхнюю границу поиска : 4
Введите допустимую погрешность : 0.00005
Исходное уравнение имеет вид :
1x^3+(-6)x^2+(-9)x+(58)=0
Первая производная имеет вид :
f'(x)=3x^2+(-12)x+(-9)
Вторая производная имеет вид :
f''(x)=6x+(-12)
-------------------------------------------------
| Xn | f(Xn) | |f(Xn)|/m |
-------------------------------------------------
| 3| 4| 0.4444444444|
| 3.222222222| 0.159122085| 0.01768023167|
| 3.231855174| 0.000341137633|3.790418145e-05|
-------------------------------------------------
Пример №3
![]()
Программа для решения кубических уравнений методом касательных (метод Ньютона).
Кубическое уравнение имеет вид
a1*x^3+a2*x^2+a3*x+a4=0
Введите значение коэффициента a[1] : 1
Введите значение коэффициента a[2] : -6
Введите значение коэффициента a[3] : -9
Введите значение коэффициента a[4] : 58
Необходимо указать интервал поиска решения.
Введите нижнюю границу поиска : 5
Введите верхнюю границу поиска : 6
Введите допустимую погрешность : 0.00005
Исходное уравнение имеет вид :
1x^3+(-6)x^2+(-9)x+(58)=0
Первая производная имеет вид :
f'(x)=3x^2+(-12)x+(-9)
Вторая производная имеет вид :
f''(x)=6x+(-12)
-------------------------------------------------
| Xn | f(Xn) | |f(Xn)|/m |
-------------------------------------------------
| 6| 4| 0.6666666667|
| 5.851851852| 0.2601229487| 0.04335382479|
| 5.840787634| 0.001413241032| 0.000235540172|
| 5.840726862|4.255405933e-08|7.092343222e-09|
-------------------------------------------------
Метод итераций.
Блок-схема алгоритма
Блок-схема решения и листинг программы, реализующей этот алгоритм на языке программирования С++.
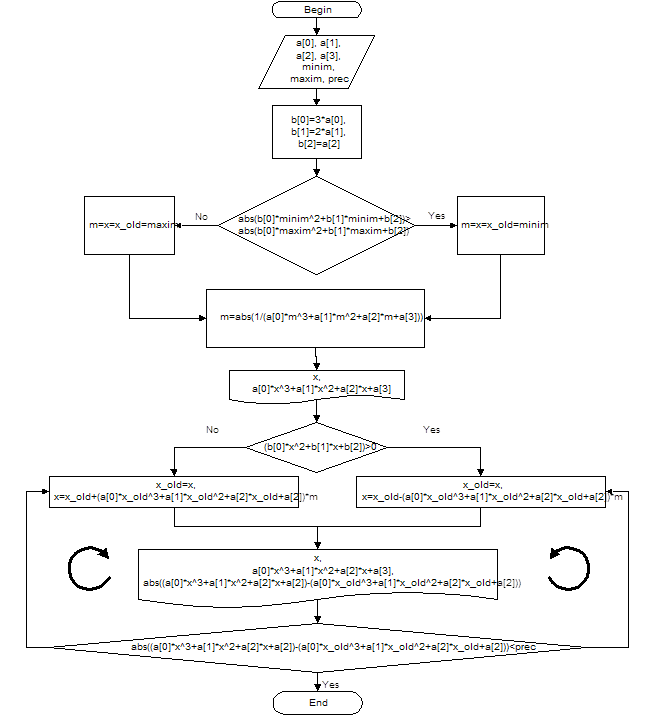
Листинг программы
//метод итераций для решения кубических уравнений
#include<math.h>
#include<iostream.h>
double a[4]={0},
b[3]={0},
prec=0.00000;
double minim=0, maxim=0;
void Hello(void);
void Input();
void Derivative();
void Calculation();
double Calc_Fun(double);
double Calc_First(double);
main(void)
{
Hello();
Input();
Derivative();
Calculation();
return 0;
}
void Hello(void)
{
cout<<"Программа для решения кубических уравнений методом итераций.nn";
}
void Input()
{
cout<<"Кубическое уравнение имеет вид"<<endl
<<"a1*x^3+a2*x^2+a3*x+a4=0"<<endl<<endl;
for (int i=0;i<4;i++)
{
cout<<"Введите значение коэффициента a["<<i+1<<"] : ";
cin>>a[i];
}
cout<<endl<<"Необходимо указать интервал поиска решения."<<endl
<<"Введите нижнюю границу поиска : ";
cin>>minim;
cout<<"Введите верхнюю границу поиска : ";
cin>>maxim;
while(minim==maxim||minim>maxim)
{
cout<<"nНижняя граница должна быть меньше верхней и не может быть ей
равна." <<endl
<<"Повторите ввод нижней границы : ";
cin>>minim;
cout<<"Повторите ввод верхней границы : ";
cin>>maxim;
}
cout<<"Введите допустимую погрешность : ";
cin>>prec;
}
void Derivative()
{
b[0]=a[0]*3;
b[1]=a[1]*2;
b[2]=a[2];
}
void Calculation()
{
double x=0, x_old=0, m=0;
cout<<"-------------------------------------------------"<<endl
<<"| Xn | f(Xn) | X(n+1)-Xn |"<<endl
<<"-------------------------------------------------"<<endl;
if(fabs(Calc_First(minim))>fabs(Calc_First(maxim))) m=x=x_old=minim;
else m=x=x_old=maxim;
m=fabs(1/Calc_First(m));
cout<<"|";
cout.width(15);cout.precision(10);
cout<<x;
cout<<"|";
cout.width(15);cout.precision(10);
cout<<Calc_Fun(x);
cout<<"| |n";
if(Calc_First(x)>0)
{
do
{
x_old=x;
x=x_old-m*Calc_Fun(x_old);
cout<<"|";
cout.width(15);cout.precision(10);
cout<<x;
cout<<"|";
cout.width(15);cout.precision(10);
cout<<Calc_Fun(x);
cout<<"|";
cout.width(15);cout.precision(10);
cout<<fabs( Calc_Fun(x) - Calc_Fun(x_old) );
cout<<"|n";
}
while(( fabs( Calc_Fun(x) - Calc_Fun(x_old) ) )>prec);
}
else
{
do
{
x_old=x;
x=x_old+m*Calc_Fun(x_old);
cout<<"|";
cout.width(15);cout.precision(10);
cout<<x;
cout<<"|";
cout.width(15);cout.precision(10);
cout<<Calc_Fun(x);
cout<<"|";
cout.width(15);cout.precision(10);
cout<<fabs( Calc_Fun(x) - Calc_Fun(x_old) );
cout<<"|n";
}
while(( fabs( Calc_Fun(x) - Calc_Fun(x_old) ) )>prec);
}
cout<<"-------------------------------------------------";
}
double Calc_Fun(double x)
{
return (a[0]*x*x*x+a[1]*x*x+a[2]*x+a[3]);
}
double Calc_First(double x)
{
return (b[0]*x*x+b[1]*x+b[2]);
}
![]()
Результаты работы программы
Пример №1
Программа для решения кубических уравнений методом итераций.
Кубическое уравнение имеет вид
a1*x^3+a2*x^2+a3*x+a4=0
Введите значение коэффициента a[1] : 1
Введите значение коэффициента a[2] : -6
Введите значение коэффициента a[3] : -9
Введите значение коэффициента a[4] : 58
Необходимо указать интервал поиска решения.
Введите нижнюю границу поиска : -4
Введите верхнюю границу поиска : -3
Введите допустимую погрешность : 0.00005
-------------------------------------------------
| Xn | f(Xn) | X(n+1)-Xn |
-------------------------------------------------
| -4| -66| |
| -3.24137931| -9.922506048| 56.07749395|
| -3.127327517| -3.12093462| 6.801571427|
| -3.091454705| -1.064778438| 2.056156183|
| -3.079215872| -0.372281515| 0.6924969227|
| -3.074936774| -0.131239433| 0.241042082|
| -3.073428275| -0.04639844126| 0.08484099175|
| -3.07289496| -0.01642029825| 0.02997814301|
| -3.072706221|-0.005813178631| 0.01060711962|
| -3.072639403|-0.002058264249| 0.003754914382|
| -3.072615744|-0.000728799396| 0.001329464852|
| -3.072607367|-0.000258060628|0.0004707387678|
| -3.072604401|-9.137721784e-0|0.0001666834108|
| -3.072603351|-3.235601088e-0|5.902120696e-05|
| -3.072602979|-1.145703711e-0|2.089897377e-05|
-------------------------------------------------
Пример №2
![]() Программа для решения кубических уравнений методом итераций.
Программа для решения кубических уравнений методом итераций.
Кубическое уравнение имеет вид
a1*x^3+a2*x^2+a3*x+a4=0
Введите значение коэффициента a[1] : 1
Введите значение коэффициента a[2] : -6
Введите значение коэффициента a[3] : -9
Введите значение коэффициента a[4] : 58
Необходимо указать интервал поиска решения.
Введите нижнюю границу поиска : 3
Введите верхнюю границу поиска : 4
Введите допустимую погрешность : 0.00005
-------------------------------------------------
| Xn | f(Xn) | X(n+1)-Xn |
-------------------------------------------------
| 3| 4| |
| 3.222222222| 0.159122085| 3.840877915|
| 3.231062338| 0.01338370012| 0.1457383849|
| 3.231805877| 0.001151957391| 0.01223174272|
| 3.231869875|9.934183961e-05| 0.001052615552|
| 3.231875394|8.568402322e-06|9.077343728e-05|
| 3.23187587|7.390497921e-07| 7.82935253e-06|
-------------------------------------------------
Пример №3
![]()
Программа для решения кубических уравнений методом итераций.
Кубическое уравнение имеет вид
a1*x^3+a2*x^2+a3*x+a4=0
Введите значение коэффициента a[1] : 1
Введите значение коэффициента a[2] : -6
Введите значение коэффициента a[3] : -9
Введите значение коэффициента a[4] : 58
Необходимо указать интервал поиска решения.
Введите нижнюю границу поиска : 5
Введите верхнюю границу поиска : 6
Введите допустимую погрешность : 0.00005
-------------------------------------------------
| Xn | f(Xn) | X(n+1)-Xn |
-------------------------------------------------
| 6| 4| |
| 5.851851852| 0.2601229487| 3.739877051|
| 5.842217669| 0.0346921878| 0.2254307609|
| 5.840932773| 0.004788677115| 0.02990351069|
| 5.840755414|0.0006639855431| 0.004124691572|
| 5.840730822|9.212373716e-05|0.0005718618059|
| 5.84072741|1.278267885e-05|7.934105832e-05|
| 5.840726937|1.773688694e-06|1.100899016e-05|
-------------------------------------------------
![]()
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ ТАТАРСТАН
АЛЬМЕТЬЕВСКИЙ НЕФТЯНОЙ ИНСТИТУТ
Кафедра информатики
Курсовая работа
На тему: метод касательных (метод Ньютона)
Работу выполнил студент гр. 52-61
Низамова Г.Н.
Проверил: Борганова Э.М.
Альметьевск 2003 г.
Похожие работы
-
Решение нелинейных уравнений
ЧИСЛЕННОЕ . 1п. Общий вид нелинейного уравнения F(x)=0 Нелинейные уравнения могут быть двух видов: Алгебраические anxn + an-1xn-1 +… + a0 = 0 Трансцендентные- это уравнения в которых х является аргументом
-
Расчетно-графическая работа
§1. ЧИСЛЕННОЕ РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ. 1п. Общий вид нелинейного уравнения F(x)=0 Нелинейные уравнения могут быть двух видов: Алгебраические
-
Вычислительная техника и программирование
Построение интерполяционного полинома Ньютона по значениям функции в узлах согласно методу Лагранжа. Составление алгоритмов решения задачи, их реализация на программном уровне на языке Turbo Pascal. Представление результатов работы программы Polinom.
-
Чисельне інтегрування та наближення функцій поліномами вищого порядку
Чисельне інтегрування, формула Сімпсона, значення інтегралу від функцій та формули трапецій. Знаходження коренів рівняння методом Ньютона. Наближення функцій поліномами вищого порядку. Метод Ейлера та його модифікації. Визначення похибок розрахунків.
-
Разработка программного обеспечения для решения уравнений с одной переменной методом Ньютона (касательных)
Программный продукт, способный решать уравнения с одной переменной методом Ньютона (касательных). Он прост в эксплуатации, имеет интуитивно понятный интерфейс, выстраивает график уравнения, что очень важно для пользователя. Реализация решений в программе.
-
Итерационные методы решения нелинейных уравнений
Решение нелинейных уравнений методом простых итераций и аналитическим, простым и модифицированным методом Ньютона. Программы на языке программирования Паскаль и С для вычислений по вариантам в порядке указанных методов. Изменение параметров задачи.
-
Решение нелинейных уравнений
Сравнительный анализ итерационных методов решения нелинейных алгебраических и трансцендентных уравнений. Простейший алгоритм отделения корней нелинейных уравнений. Метод половинного деления. Геометрический смысл метода Ньютона. Метод простой итерации.
-
Приближенное вычисление значений определенного интеграла
Сущность и особенности применения метода средних треугольников. Порядок расчета по методу трапеций и Ньютона-Котеса. Формула Чебышева и значения узлов ее квадратуры. Составление блок-схемы программы и ее основных процедур различными численными методами.
-
Нахождение корней уравнения методом Ньютона (ЛИСП-реализация)
Определение недостатков итерационного численного способа нахождения корня заданной функции (метод Ньютона). Рассмотрение основ математического и алгоритмического решения поставленной задачи, ее функциональной модели, блок-схемы и программной реализации.
-
Решение систем нелинейных алгебраических уравнений методом Ньютона
Модифицированный метод Ньютона при заданных начальных условиях, где задаётся погрешность вычисления. Вычисления корня уравнения при помощи программы. Построения графика зависимости приближений двух координат, при котором задаются промежутки и константы.