Название: Чисельне інтегрування та наближення функцій поліномами вищого порядку

Вид работы: контрольная работа

Рубрика: Информатика и программирование

Размер файла: 1.79 Mb

Скачать файл: referat.me-136262.docx

Краткое описание работы: Чисельне інтегрування, формула Сімпсона, значення інтегралу від функцій та формули трапецій. Знаходження коренів рівняння методом Ньютона. Наближення функцій поліномами вищого порядку. Метод Ейлера та його модифікації. Визначення похибок розрахунків.

Чисельне інтегрування та наближення функцій поліномами вищого порядку

Міністерство освіти і науки України

Житомирський державний технологічний університет

Кафедра ТМ та КТС

Група ЗІМ 03-1т

Курсова робота

з інформатики

на тему: «Чисельне інтегрування. НАБЛИЖЕННЯ ФУНКЦІЙ ПОЛІНОМАМИ ВИЩОГО ПОРЯДКУ»

Житомир

Зміст

Завдання № 1. – Чисельне інтегрування. Формула трапецій та формула Сімпсона

Завдання № 2. – Знаходження коренів рівняння методом Ньютона

Завдання № 3,4. – Наближення функцій поліномами вищого порядку

Завдання № 5. – Метод Ейлера. Модифікації метода Ейлера

Завдання № 1

Чисельне інтегрування. Формула трапецій та формула Сімпсона

Розрахувати за допомогою формул трапецій та Сімпсона значення інтегралу від функції y=f(x)= a₀ +a₁ x+a₂ x² +a₃ x³ +a ₄ x⁴ +a₅ x⁵ з точністю до п’ятого знака. Визначити похибки розрахунків для різних значень n – e8 та e4

Вихідні дані:

Варіант	a0	a1	a2	a3	a4	a5
2	1	0.9	0.8	0.7	0.5	2.3

Реалізація у MS Excel:

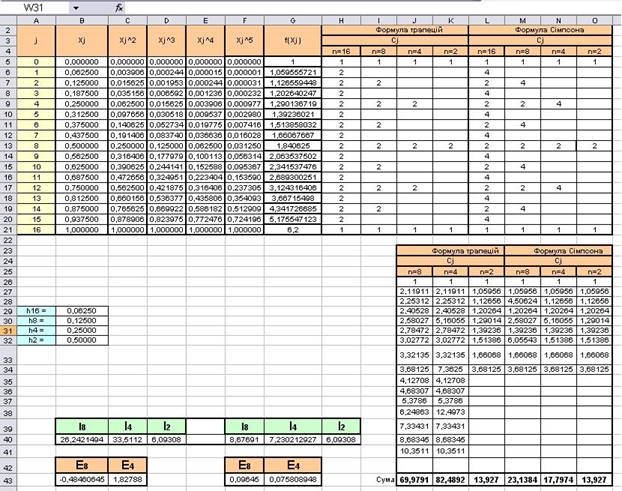
Хід виконання:

Визначений інтеграл чисельно рівний площі криволінійної трапеції, яка описується кривою y = f(x), віссю х та двома прямими, паралельними осі ординат x = a, x = b. Тому знаходження розв’язку інтеграла є визначення відповідної площі.

Розіб’ємо відрізок [a, b] = [0, 1] на n=16 рівних елементарних трапецій із площами s. Величину D, що дорівнює основі кожної із елементарних трапецій, позначимо буквою h і називатимемо кроком квадратурної формули, який визначається з формули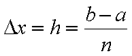

Таким чином, шукана формула трапецій має вигляд

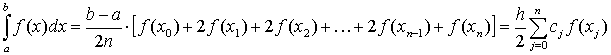
де c_j = 1,2,2,2,….2,1.

Для формули парабол (Сімпсона) замість двох прямолінійних трапецій розглядається одна трапеція, яка обмежена параболічною дугою

Елементарна площа визначається інтегралом

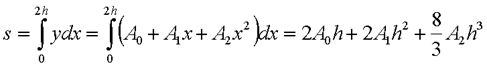
Враховуючи, що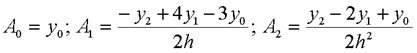

Отримаємо формулу парабол (Сімпсона)

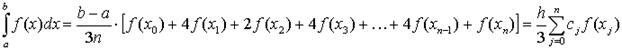
де c_j = 1, 4, 2, 4, 2,…..2, 4, 1.

У формулі трапецій n є довільним числом, у формулі Сімпсона воно повинно бути парним.

Завдання № 2

Знаходження коренів рівняння методом Ньютона

Визначити всі дійсні корені поліному P(x)=a₀ +a₁ x+a₂ x² +a3x³ за допомогою методів Ньютона (дотичних) та методу „січних”. Результати розрахунків звести у таблицю.

Вихідні дані:

Варіант	a0	a1	a2	a3
2	1,3	-7	-4	-4

Реалізація у MS Excel:

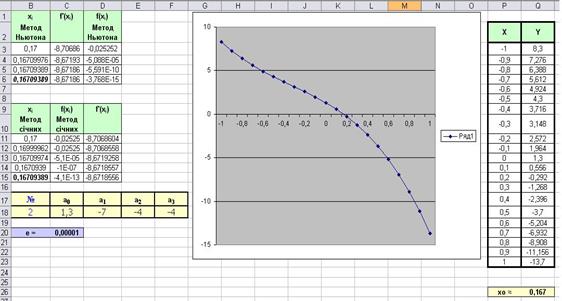
Хід виконання:

1. Будуємо графік заданої функції та визначаємо з нього приблизне значення кореня х_{0 ≈} 0,17

2. Проводимо уточнення коренів за методом Ньютона та січних з точністю e=10^-5 .

В розрахунках наближене значення похідної знаходиться за формулою:

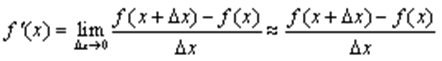
При уточненні коренів рівняння методом Ньютона користуємось наступними формулами:

Чергове k-е наближення:

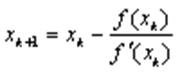
В якості малої величини беремо задану точність обчислень , тоді розрахункова формула має вигляд:

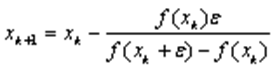
При уточненні коренів рівняння методом січних користуємось наступними формулами:

Для першого наближення:

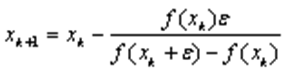
Для подальших наближень:

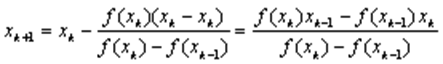
Завдання № 3,4

Наближення функцій поліномами вищого порядку

Функція y=f(x) задана таблицею значень у точках . Використовуючи метод найменших квадратів (МНК), знайти многочлен найменшого середньоквадратичного наближення оптимальної степені m=m*. За оптимальне значення m* прийняти ту степінь многочлена, починаючи з якої величина 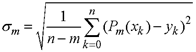стабілізується або починає зростати.

Вихідні дані:

Варіант 2
x	0	0,375	0,563	0,75	1,125	1,313	1,5	1,690	1,875	2,063	2,25	2,438	2,625	2,813	3
y	4.568	3,365	2,810	2,624	0,674	0,557	0,384	-0,556	-1,44	-1,696	-1,91	-2,819	-3,625	-3,941	-4,367

Хід виконання:

1. Задаємо вектори x та y вихідних даних.

2. Використовуючи метод найменших квадратів, знаходимо многочлени Pm, m = 0,1,2... Розраховуємо відповідні їм значення .

3. Будуємо гістограму залежності від m, на основі якої вибратємо оптимальну степінь m* многочлена найкращого середньоквадратичного наближення.

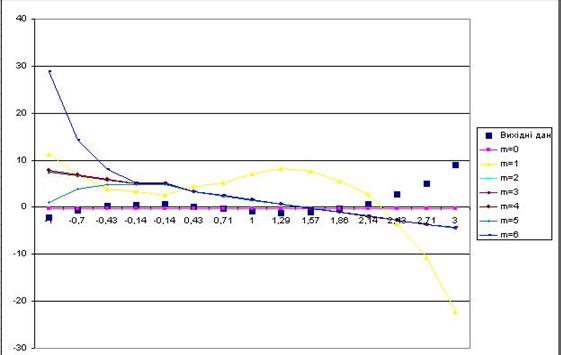
4. На одному графіку будуємо многочлени P_m , m = 0,1,2,..., m*, і точковий графік вихідної функції.

Реалізація у MS Excel:

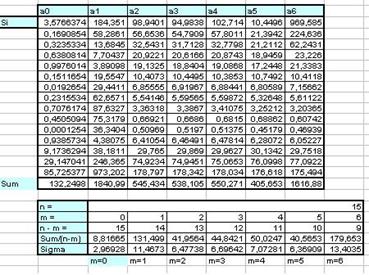
Визначаємо матрицю Х як суму відповідних х_і у відповідних степенях та у_і *х_і ^j

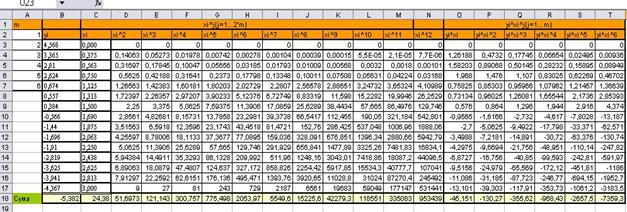
За допомогою отриманих даних, будуємо, для полінома кожної степені, відповідну матрицю Х:

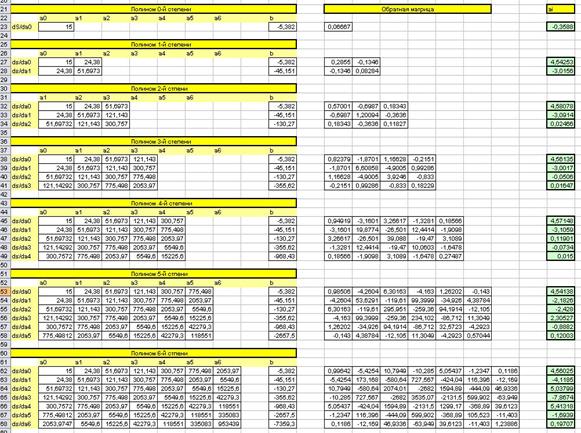
Визначаємо обернені матриці Х^-1 до відповідних матриць Х, використовуючи вбудовану функцію Excel МОБР(....).

Визначаємо коефіцієнти відповідних поліномів, для чого визначаємо добуток матриць Х^-1 та B, використовуючи вбудовану функцію МУМНОЖ(....).

Використовуючи визначені коефіцієнти поліномів а_і , визначаємо значення даних поліномів у кожній точці х_і .

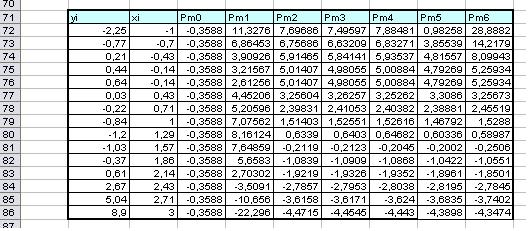
Будуємо графік отриманих поліномів та вихідних даних: вихідні дані – точковий графік, розрахункові дані – лініями різного типу.

Визначаємо величину для кожного полінома та будуємо гістограму:

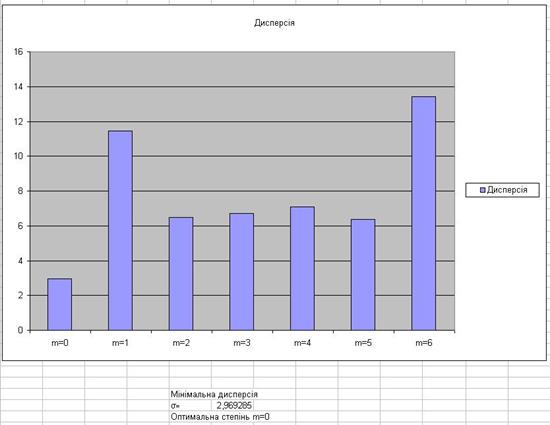
Вже по побудованій гістограмі можна робити висновки про оптимальність степені полінома для апроксимації вихідних даних (мінімальне значення , але визначимо мінімум за допомогою функції МИН(...) . І по отриманому значенню робимо висновок про оптимальну степінь апроксимуючої функції

Завдання № 5

Метод Ейлера. Модифікації метода Ейлера

Використовуючи метод Ейлера, скласти на відрізку [а, b] таблицю значень інтегралу диференційного рівняння y' = f (x, y), що задовольняє початковим умовам (x₀ , y₀ ), вибираючи крок інтегрування h, де

y(x_i +h)=y(x_i )+h·y'(x_i )

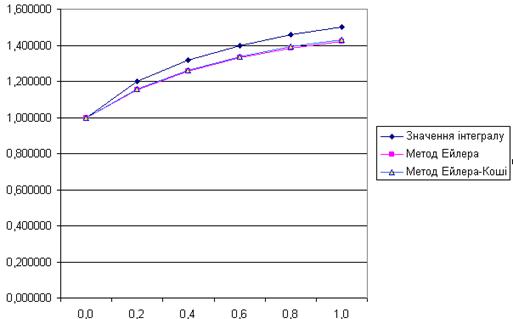
Розв’язати попереднє диференційне рівняння y' =f(x, y) вдосконаленим методом ломаних та вдосконаленим методом Ейлера-Коші.

Вихідні дані:

Варіант	h	[a, b]	(x0 , y0 )
2	0,2	[0;1]	(0;1)

Реалізація у MS Excel:

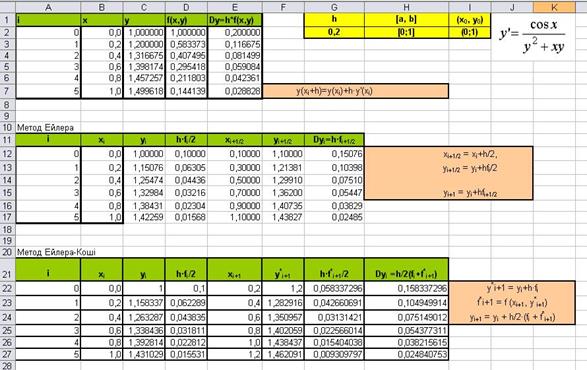
Графіки розрахованих даних: