Название: Определение динамических характеристик системы

Вид работы: реферат

Рубрика: Информатика и программирование

Размер файла: 46.23 Kb

Скачать файл: referat.me-139548.docx

Краткое описание работы: Понятие идентификацией систем. Взаимная корреляционная функция между входом и выходом системы. Определение импульсной переходной функции объекта по статистическим характеристикам, а также импульсной переходной функции по детерминированным характеристикам.

Определение динамических характеристик системы

Министерство образования Республики Беларусь

Учреждение образования

''Белорусский государственный университет информатики и радиоэлектроники''

кафедра информационные технологии автоматизированных систем

РЕФЕРАТ

на тему:

«Определение динамических характеристик системы»

Минск, 2008

СОДЕРЖАНИЕ

1. Взаимная корреляционная функция между входом и выходом системы

2. Определение импульсной переходной функции объекта по статистическим характеристикам

3. Определение импульсной переходной функции по детерминированным характеристикам

Определение характеристик системы по экспериментальным данным называется идентификацией систем. Этот важный класс задач теории управления располагает большим набором методов, основанных на методах анализа систем.

Среди них важное место занимают методы, которые связаны с подачей на вход определенных воздействий. Зная взаимосвязь между входом и выходом системы во временной и частотной областях, можно определить переходную или частотную характеристику. Например, реакция на единичное ступенчатое воздействие является единичной переходной функцией.

Однако определение переходных и передаточных функций линейных систем или объектов управления посредством подачи на ее вход искусственных воздействий определенного вида (импульсов, ступенчатых воздействий, гармоник) и замера реакции системы на эти воздействия не всегда возможно.

Причин тому может быть несколько.

Во-первых, нередко подача на вход системы невозможна или нежелательна, так как это ведет к нарушению нормального хода технологического процесса. И в то же время необходимо определить характеристики системы в режиме ее нормальной эксплуатации.

Во-вторых, очень часто на входные воздействия специального вида накладываются случайные неконтролируемые воздействия (шумы и помехи), в результате чего оказываются невозможным точное определение динамических характеристик системы по реакции на типовые воздействия.

В этих случаях прибегают к методам определения характеристик системы, основанным на взаимосвязи статистических характеристик процессов, протекающих в системе. Приведенные выше выражения не всегда удобны. Приведем дополнительные сведения на этот счет.

1 Взаимная корреляционная функция между входом и выходом системы

Процессы на входе и выходе системы с импульсной переходной функцией связаны уравнением свертки, которое можно записать в виде

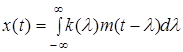. (1)

Если же дополнительно к управляющему воздействию на систему действует возмущающее воздействие (помеха) , так что - импульсная переходная функция по помехе, то в приведенном выше выражении появляется дополнительное слагаемое

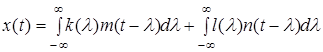. (2)

Пусть внешние воздействия являются стационарными случайными процессами и, как следствие, таковым же является выходной процесс .

Для центрированных процессов (при нулевых математических ожиданиях) определим взаимную корреляционную функцию входного и выходного процессов как математическое ожидание произведения этих процессов, один из которых сдвинут по времени

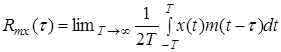. (3)

Здесь, как и раньше, использовано усреднение по времени вместо усреднения по множеству.

Подставим сюда выражение выходного процесса (2)

.

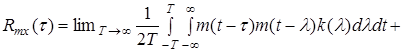
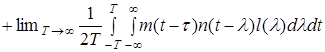Изменим порядок интегрирования

.

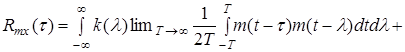
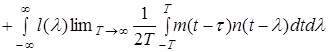Внутренние интегралы здесь представляют выражения корреляционных функций. Поэтому последнее выражение можно представить в виде:

.

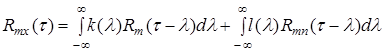Если помеха не коррелирована с управляющим воздействием , что чаще всего и бывает, то последнее слагаемое равно нулю и

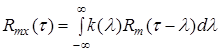. (4)

Полученное выражение представляет собой интеграл свертки. Оно аналогично выражению (1). Если рассматривать корреляционную функцию как входное воздействие, а взаимную корреляционную функцию – как выходной процесс, то указанная аналогия станет очевидной.

Заметим, что в окончательном выражении (4) не фигурируют ни характеристики помехи, ни импульсная переходная функция по помехе. Не отражен даже сам факт наличия помехи.

Если бы вывод этого выражения был основан на использовании выражения (1), а не (2), т.е. в предположении, что помеха отсутствует, то и тогда было бы получено выражение связи (4).

Этим не исчерпываются замечательные свойства полученного выражения. Предположим, что на входе системы действует «белый шум», т.е. . Тогда по основному свойству d - функции

.

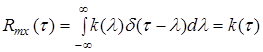Другими словами, если на вход системы подавать «белый шум», то взаимно корреляционная функция будет численно равна импульсной переходной функции системы.

Это чисто теоретический результат, но он имеет большое практическое значение. Как известно, «белый шум» - это абстрактное математическое понятие, идеализация случайного процесса, спектральная плотность которого одинакова для любой частоты. Такого процесса в природе не существует: для его генерации потребовался бы источник бесконечно большой мощности. Однако к такой идеализации прибегают всякий раз, когда изменением спектральной плотности в полосе пропускания системы можно пренебречь.

Но даже с учетом этого обстоятельства полученный результат имеет большое значение, потому что чем ближе спектральная плотность к «белому шуму», тем ближе взаимная корреляционная функция к импульсной переходной функции.

2 Определение импульсной переходной функции объекта по статистическим характеристикам

Если входной процесс не может считаться «белым шумом», для определения импульсной переходной функции необходимо решить интегральное уравнение (4).

Рассчитывать на аналитическое решение данного уравнения после экспериментального определения корреляционных функций и в подавляюще большинстве случаев не приходится. Для этого применяются численные методы.

Для решения различного рода уравнений численными методами необходима дискретизация задачи. В данном случае для этого достаточно заменить интеграл в выражении (4) конечной суммой.

При вычислении интеграла по формуле прямоугольников это происходит естественным образом. Для применения упомянутой формулы интервал интегрирования разбивают на достаточно малые подинтервалы длиной Т , на каждом из которых подынтегральная функция мало изменяется.

В качестве интервала интегрирования возьмем интервал (0, L). Нижняя граница определяется условием физической осуществимости: при отрицательных значениях аргумента импульсная функция равна нулю, а конечный верхний предел определяется условием устойчивости системы: импульсная переходная функция устойчивой системы должна стремиться к нулю.

Следовательно, найдется такое значение аргумента импульсной переходной функции L, что при больших значениях она пренебрежимо мала. Далее, разобьем интервал (0, L) на N одинаковых по длине подинтервалов, каждый из которых имеет длину T .

После этого уравнение (4) можно с достаточной степенью точности представить в виде суммы

.

Полагая , получим систему N уравнений относительно N неизвестных

. (5)

Обозначив , , и учитывая четность корреляционной функции , полученную систему уравнений можно записать в развернутом

;

;

………………………………….…….

.

или матричном виде

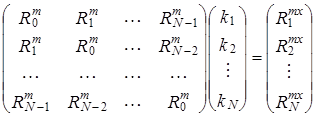
В результате решения этой системы уравнений можно получить значения импульсной переходной функции при .

3 Определение импульсной переходной функции по детерминированным характеристикам

Из уравнения связи между входным и выходным процессами в детерминированном случае также можно получить систему уравнений относительно значений импульсной переходной функции.

Действительно, связь между входом и выходом во временной области описывается уравнением свертки (1). Оно до сих пор рассматривалось как выражение выходной координаты через входную, как интегральный оператор, который ставит входному процессу в соответствие некоторый выходной процесс.

Описание импульсной переходной функции и входного процесса в этом случае должно быть известно.

Если же известными являются другие две компоненты из трех: входного и выходного процесса и требуется определить импульсную переходную характеристику, то на данное выражение следует смотреть как на интегральное уравнение.

Оно может быть решено и в результате получено значение импульсной переходной функции.

Действительно, повторив рассуждения по выводу уравнения (5) из уравнения (4), из уравнения (1) получим уравнение

.

При получим отсюда систему N уравнений относительно N неизвестных . Обозначив , , , полученную систему уравнений можно записать в виде

.

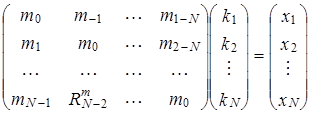Различие между двумя этими системами уравнений не только в том, что в одном случае матрица системы уравнений симметричная, а в другом – нет. Основное различие в степени влияния шумов на результат вычислений.

Если шумы значительны, то ошибки при определении импульсной переходной функции по детерминированным характеристикам могут быть очень велики.

В то же время, если шумы (помехи) при определении соответствия межу входом и выходом некоррелированы с входным воздействием, то они могут иметь любую интенсивность.

Точность результата вычислений от этого не изменится, но при этом необходимо оперировать не значениями самих сигналов, а их корреляционными функциями.

Если же помехи отсутствуют, то нет необходимости прибегать к статистическим методами. В детерминистическом случае наряду с рассмотренным только что подходом к определению импульсной переходной функции существует еще один, обладающий определенными достоинствами по сравнению с только что рассмотренным.

Они связаны с большей простотой уравнения, которое необходимо решать для определения дискретных значений импульсной переходной функции.

Как уже отмечалось, связь между входным и выходным процессами выражается не только интегралом свертки (1), но и интегралом

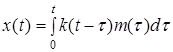
В свое время были даны доказательства возможности замены переменного верхнего предела бесконечным значением. В данном случае в этом нет необходимости. Наоборот, всякое сужение области интегрирования приводит к упрощению системы уравнений, которую необходимо решать.

Заменим интеграл конечной суммой точно так же, как это делалось ранее. Получим

.

Здесь так же все процессы рассматриваются в дискретные моменты времени . Полученное выражение здесь также можно рассматривать как систему N уравнений относительно N неизвестных , но лучше рассматривать его как рекуррентное уравнение.

Обозначив , , , полученную систему уравнений для различных, последовательно увеличивающихся значениях n можно записать в виде

;

;

;

………………………….

Отсюда

;

;

;

………………………………

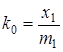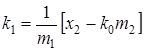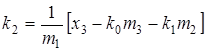Отсюда уже видно, что значения импульсной переходной характеристики в дискретные моменты времени могут быть определены последовательно, друг за другом, до тех пор, пока они не станут пренебрежимо малыми.

ЛИТЕРАТУРА

1. Мирошник И.В. Теория автоматического управления. Линейные системы. - СПб.: Питер, 2005.

2. Филлипс Ч., Харбор Р. Системы управления с обратной связью. М.: Лаборатория Базовых Знаний, 2007.

3. Методы классической и современной теории автоматического управления в 3-х т. Т.1: Анализ и статистическая динамика систем автоматического управления / Под ред. Н.Д. Егупова. – Изд. МГТУ им. Н.Э. Баумана, 2005.