Referat.me
/ / Точность систем автоматического управления

Название: Точность систем автоматического управления

Вид работы: реферат

Рубрика: Информатика и программирование

Размер файла: 56.83 Kb

Скачать файл: referat.me-139811.docx

Краткое описание работы: Порядок оценки точности системы автоматического управления по величине установившейся ошибки при типовых воздействиях, механизм ее повышения. Разновидности ошибок и методика их вычисления. Определение ошибок по виду частотных характеристик системы.

Точность систем автоматического управления

Точность систем автоматического управления

1. Точность САУ

Точность САУ оценивается в установившемся режиме по величине установившейся ошибки при типовых воздействиях. При анализе точности систем рассматривается установившийся режим, так как текущее значение ошибки резко меняется вследствие наличия переходных процессов и не может быть мерой точности.

Рассмотрим систему представленную на рис. 1.


На схеме приняты следующие обозначения: Kу (p) – передаточная функция устройства управления; K0 (p) – передаточная функция объекта управления; f – возмущающее воздействие; x – задающее воздействие; y – регулируемая величина.

Ошибка по задающему воздействию равна e (t) = x(t) – y(t).

Изображение ошибки равно

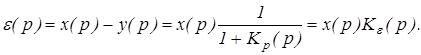(1)

Установившееся значение ошибки определяется с помощью теоремы о конечном значении функции


(2)

Ошибка по возмущению воздействию равна e (t) = – y(t) , т.е. равна изменению регулируемой величины под действием возмущения при отсутствии входного воздействия.

В общем случае как задающее, так и возмущающее воздействия являются сложными функциями времени. При определении ошибок пользуются типовыми воздействиями, которые с одной стороны соответствуют наиболее тяжелым режимам работы системы и, вместе с тем, достаточно просты для аналитических исследований.

Кроме того, типовые воздействия удобны для сравнительного анализа различных систем, и соответствуют наиболее часто применяемым законам изменения управляющих и возмущающих воздействий.

2. Типы ошибок

Различают следующие типы ошибок:

– статическая ошибка (ошибка по положению) – ошибка, возникающая в системе при отработке единичного воздействия;

– кинетическая ошибка (ошибка по скорости) – ошибка, возникающая в системе при отработке линейно – возрастающего воздействия;

– инерционная ошибка (ошибка по ускорению) – ошибка, возникающая в системе при отработке квадратичного воздействия.

С точки зрения ошибок, системы можно классифицировать на статические и астатические.

Передаточная функция статической системы имеет вид

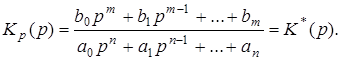(3)


Передаточная функция астатической системы имеет вид

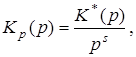(4)

где K*(p) – передаточная функция, не содержащая интегрирующих звеньев а s – порядок астатизма.

Рассмотрим статическую систему (s = 0). Определим выражения для соответствующих ошибок.

1. Статическая ошибка определяется следующим соотношением

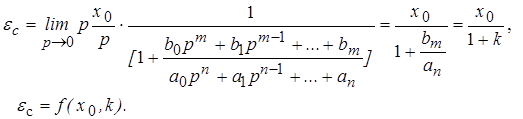(5)

2. Кинетическая ошибка определяется следующим соотношением

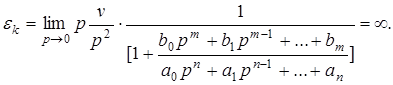(6)

3. Инерционная ошибка определяется следующим соотношением

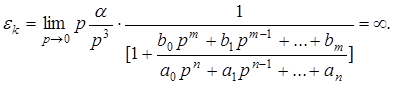(7)

Эта система не может быть использована как синхронно – следящая, так как кинетическая ошибка стремится к бесконечности.

Пример 1. Для заданной системы (рис. 2) определить установившиеся ошибки


Решение: Определим установившиеся ошибки.

1. Статическая ошибка определяется следующим соотношением

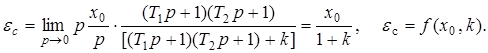
2. Кинетическая ошибка определяется следующим соотношением

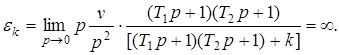
3. Инерционная ошибка определяется следующим соотношением

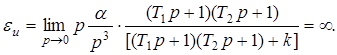
На графиках это можно изобразить следующим образом (рис. 3)



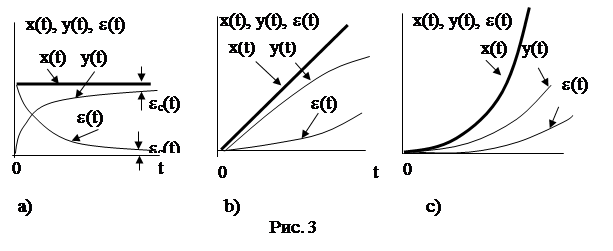
Рассмотрим астатическую систему первого порядка (s = 1).

Определим выражения для установившихся ошибок.

1. Статическая ошибка определяется следующим соотношением

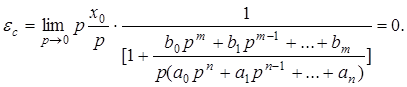(8)

2. Кинетическая ошибка определяется следующим соотношением

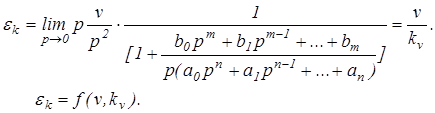(9)

3. Инерционная ошибка определяется следующим соотношением

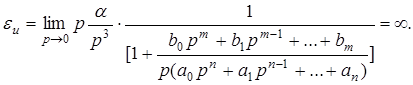(10)


Эта система может быть использована как синхронно – следящая, так как кинетическая ошибка равна нулю.

Пример 2. Для заданной системы (рис. 4) определить ошибки


Решение: Определим выражения для ошибок.

1. Статическая ошибка определяется следующим соотношением

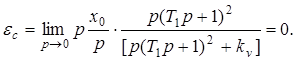
2. Кинетическая ошибка определяется следующим соотношением

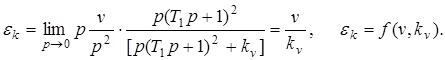
Т.е. ошибка является функцией скорости изменения входного воздействия и коэффициента усиления системы.

3. Инерционная ошибка определяется следующим соотношением


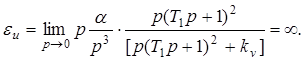
Графики изменения ошибок приведены на рис. 5.



а) b) c)

Рис. 5
Рассмотрим астатическую систему второго порядка (s = 2).

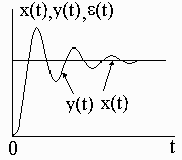Определим выражения для ошибок.

1. Статическая ошибка определяется следующим соотношением

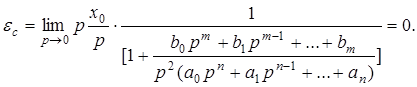(11)

2. Кинетическая ошибка определяется следующим соотношением

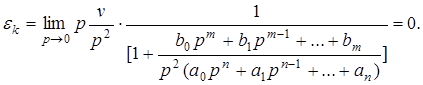(12)

3. Инерционная ошибка определяется следующим соотношением

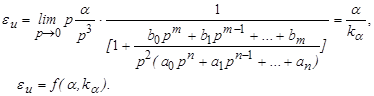(13)


Инерционная ошибка является функцией ускорения изменения входного воздействия и коэффициента усиления системы.

Эта система может быть использована как синхронно – следящая, так как кинетическая ошибка равна нулю.

Пример 3. Для заданной системы (рис. 6) определить установившиеся ошибки


Решение: Определим выражения для ошибок.

1. Статическая ошибка определяется следующим соотношением

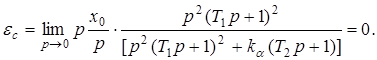
2. Кинетическая ошибка определяется следующим соотношением

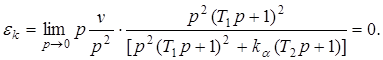
3. Инерционная ошибка определяется следующим соотношением


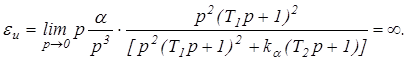
На графиках это можно изобразить следующим образом (рис. 7)

b) b) c)

Рис. 7

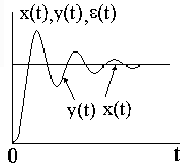
Для повышения точности САУ необходимо увеличивать коэффициент усиления системы и порядок астатизма, но это может привести к неустойчивости, т.е. требования по точности и устойчивости противоречивы.

Определение ошибок по виду частотных характеристик САУ

О характере ошибок можно судить по низкочастотной ветви любой частотной характеристики (АФХ, ЛАЧХ, ФЧХ), так как низкочастотная ветвь характеризует статику системы. Частотные характеристики систем с различным порядком астатизма приведены в таблице 1.

Таблица 1

АФХ ЛАЧХ ФЧХ

s=0;

ec =x0 /(1+k);

eк =¥;

eи =¥.

+j

-1 +

s =1;

ec =0;

eк =v/kv ;

eи =¥.

+j

-1 +

s = 1;

ec =0;

eк =0;

eи = a/ka .

+j

-1 +

3. Ошибки по возмущению

Установившаяся ошибка по возмущению равна

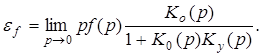(14)

Рассмотрим примеры

Пример 4. Для заданной системы (рис. 9) со статическим регулятором определить ошибку по возмущению.


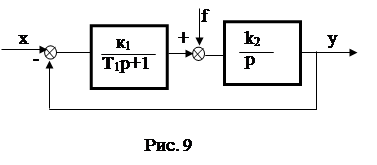Решение: Пусть f(p) = f0 /p , при этом ошибка равна


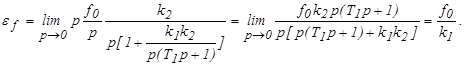
При статическом регуляторе установившаяся ошибка по возмущению зависит от амплитуды воздействия и коэффициента усиления регулятора т.е. e f = f(f0 , k1 ).

Пример 5. Для заданной системы (рис. 10) с астатическим регулятором, определить ошибку по возмущению.


Решение: Пусть f(p) = f0 /p , при этом ошибка равна

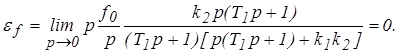
При астатическом регуляторе ошибка по возмущению равна нулю.

Литература

1. Вероятностные методы в вычислительной технике. Под ред. А.Н. Лебедева и Е.А. Чернявского – М.: Высш. Шк., 1986. -312 с.

2. Зайцев Г.Ф. Теория автоматического управления и регулирования. – 2-е изд., перераб. и доп. Киев, Издательство Выща школа Головное издательство, 198

3. Справочник по теории автоматического управления. /Под ред. А.А. Красовского – М.: Наука, 1987. – 712 с.

4. Теория автоматического управления: Учебник для вузов. Ч1 / Под ред. А.А. Воронова – М.: Высш. Шк., 1986. – 367 с.

5. Теория автоматического управления: Учебник для вузов. Ч2 / Под ред. А.А. Воронова – М.: Высш. Шк., 1986. -504 с.

6. Шандров Б.В. Технические средства автоматизации: учебник для студентов высших учебных заведений. Москва, Издательский центр «Академия», 2007.

Похожие работы