Название: Принципы построения систем автоматического управления

Вид работы: контрольная работа

Рубрика: Информатика и программирование

Размер файла: 52.58 Kb

Скачать файл: referat.me-134806.docx

Краткое описание работы: Теория автоматического управления как наука, предмет и методика ее изучения. Классификация систем автоматического управления по различным признакам, их математические модели. Дифференциальные уравнения систем автоматического управления, их решения.

Принципы построения систем автоматического управления

Предмет:

"Теория автоматического управления"

Тема:

"Принципы построения систем автоматического управления"

1. Основные понятия и определения

Теория автоматического управления (ТАУ) – наука о принципах построения, методах расчета и исследования автоматических систем.

ТАУ рассматривает класс систем, основой функционирования которых является процесс преобразования энергии (в отличие от информационных систем – преобразующих информацию).

Системой автоматического управления (САУ) называется совокупность управляемого объекта и устройства управления, взаимодействующих в соответствии с заданным законом (алгоритмом) управления.

Типовая, структурная схема сис-темы автоматического управления приведенана рис.

Управлением в технических системах называется преднамеренное воздействие на управляемый объект, обеспечивающее достижение поставленной цели.

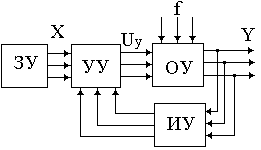
Рис. 1

2. Классификация САУ

Системы автоматического управления можно классифицировать по различным признакам:

1. По характеру изменения выходной величины:

– системы автоматического регулирования (САР, стабилизации) – системы, в которых выходная величина поддерживается на постоянном уровне, определенном заранее;

– следящие системы – это системы, в которых выходная величина изменяется в соответствии с заранее неизвестной функцией, определяемой заданием;

– программные системы – это системы, в которых выходная величина изменяется в соответствии с программой определяемой заданием;

– экстремальные системы – это системы, в которых выходная величина поддерживается на уровне некоторого экстремума;

– оптимальные системы – это системы, в которых выход таков, что некоторый показатель наилучший в определенном смысле.

2. По принципу управления:

– системы с управлением по отклонению – системы, в которых управляющее воздействие вырабатывается в функции разности задающего и возмущающего воздействия. Этот принциписпользуется в замкнутых системах управления. Структурная схема системы с управлением по отклонению приведена на рис. 2а.

– системы с управлением по возмущению – системы, в которых управляющее воздействие вырабатывается в функции задающего или возмущающего воздействия. Этот принцип управления чаще всего используется в разомкнутых системах. Структура системы с управлением по возмущению приведена на рис. 2б.

– системы скомбинированным управлением – системы, в которых сочетается первый и второй принципы управления. Структура системы с комбинированным управлением приведена на рис. 2в.

б)

в)

а)

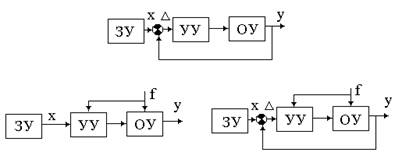
Рис. 2

3. По характеру изменения сигналов: непрерывные; дискретные.

4. По числу регулируемых величин: одномерные; многомерные.

5. По виду ошибок: статические; астатические.

6. По характеру описываемых уравнений: линейные – нелинейные; детерминированные – стохастические; стационарные – нестационарные и т.д.

Основные вопросы, которые рассматривает теория автоматического управления:

Математические модели систем автоматического управления.

2. Определение устойчивости систем управления.

3. Анализ качества систем.

4. Коррекцию систем.

5. Задачи анализа и синтеза оптимальных систем.

3. Математические модели САУ

Для описания сигналов и систем, в зависимости от используемых методов исследования, применяются различные формы их представления во временной, частотной или операторной области. Взаимосвязь между областями осуществляется с помощью преобразований Фурье и Лапласа, как показано на рис. 3.

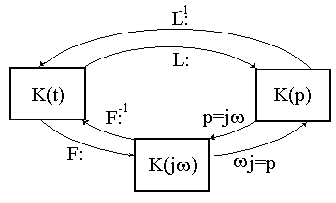
Рис. 3

Преобразование Фурье. Соответствие между временным и частотным представлением сигнала можно выразить через преобразование Фурье:

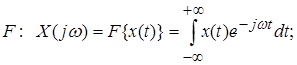(2.1)

и обратное преобразование Фурье:

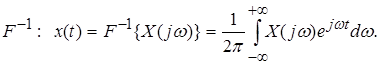(2.2)

Преобразование Лапласа. Соответствие между временным и операторным представлением сигнала можно выразить через преобразование Лапласа:

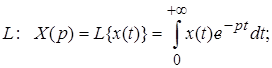(2.3)

и обратное преобразование Лапласа:

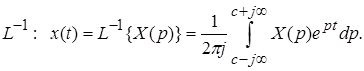(2.4)

где р = c+ j w – оператор Лапласа, c – область сходимости, x(t) – оригинал, а X(p) – изображение.

Для дискретных систем используют дискретные преобразования Лапласа и Фурье, а также ряд других преобразований (Z, W и др.).

Основные свойства (теоремы) преобразования Лапласа

Свойство линейности

(2.5)

2. Дифференцирование оригинала

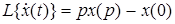, (2.6)

,

где.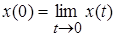

При нулевых начальных условиях

.

3. Интегрирование оригинала

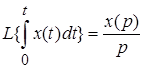. (2.7)

4. Теорема о свертке (умножения в комплексной области)

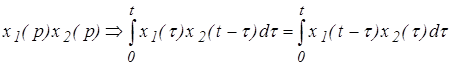. (2.8)

5. Теорема разложения.

Если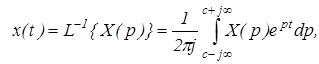 где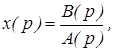

то оригинал, в соответствии с теоремой Коши о вычетах может быть определен как сумма вычетов по полюсам подынтегральной функции

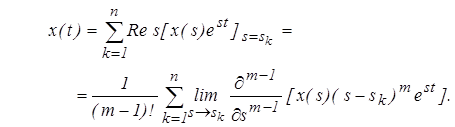(2.9)

6. Теорема о предельных значениях функции.

Начальное значение функции:. (2.10)

Конечное значение функции: . (2.11)

7. Теорема запаздывания

. (2.12)

4. Дифференциальные уравнения САУ

При математическом описании систем автоматического управления составляют уравнения статики и динамики.

Уравнения статики описывают установившиеся режимы и, как правило, являются алгебраическими.

Уравнения динамики описывают переходные процессы в системах автоматического управления и представляют собой дифференциальные, интегро-дифференциальные или разностные уравнения.

Уравнения динамики системы составляются на основе уравнений отдельных элементов, входящих в систему. Уравнения элементов записываются на основе физических законов, определяющих поведение данного элемента, чаще всего это законы сохранения энергии (Кирхгофа, Ньютона, и др.).

В качестве примера рассмотрим порядок составления уравнения динамики для RLC – четырехполюсника (рис. 4).

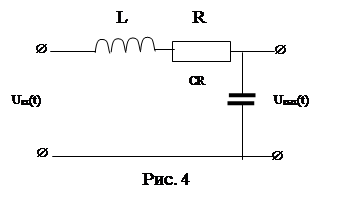В соответствии сзаконом Кирхгофа можно записать уравнения

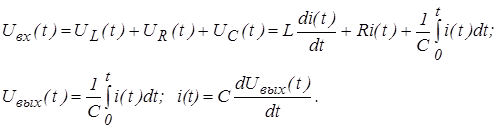
Выполнив преобразования, получим дифференциальное уравнение данной цепи.

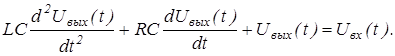
Из условия равенства нулю производных, получим уравнение статики

Линеаризация дифференциальных уравнений

Обычно дифференциальные уравнения САУ являются нелинейными вследствие нелинейности характеристик элементов системы (порог чувствительности, ограничение по мощности, трение, люфт, зазор, гистерезис и др.). Решение нелинейных уравнений существенно сложнее, чем линейных. Поэтому всегда, если это возможно, необходимо преобразовать нелинейное уравнение к приближенному линейному, т.е. выполнить линеаризацию.

Линеаризация – замена нелинейного уравнения приближенным линейным. Линеаризация возможна при следующих условиях:

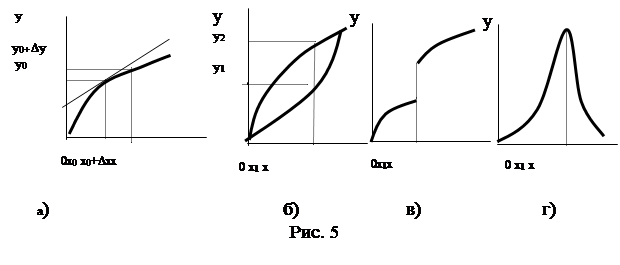
Если отклонения переменных D x и D y относительно установившихся значений x₀ и y₀ малы (рис. 5а). Это условие выполняется для широкого класса систем автоматического управления (например, для замкнутых систем).

2. Система не содержит существенно – нелинейных элементов, т.е. характеристики должны быть однозначными и не иметь разрывов 1-го или 2-го рода (рис. 5б-г).

Линеаризация осуществляется путем разложения нелинейной функции в ряд Тейлора в окрестности точки, соответствующей установившемуся режиму.

Выразим переменные x и y через их установившиеся значения x₀ и y₀ и отклонения D x и D y .

При этом

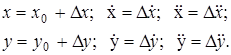(3.1)

Разложение в ряд Тейлора имеет вид:

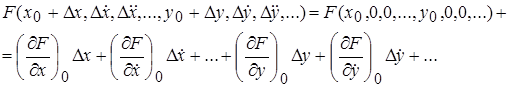(3.2)

Вычтем уравнение установившегося режима, что соответствует переносу начала координат в точку (x₀ , y₀ ), при этом получим линеаризованное уравнение:

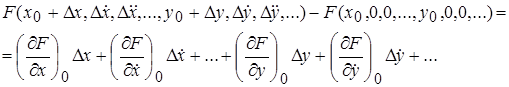(3.3)

Отличие линеаризованного уравнения от исходного нелинейного:

Линеаризованное уравнение линейное.

2. Линеаризованное уравнение приближенное.

3. Линеаризованное уравнение это уравнение в отклонениях (вариациях).

Литература

1. Автоматизированное проектирование систем автоматического управления. / Под ред. В.В. Солодовникова. – М.: Машиностроение, 1990. -332 с.

2. Бесекерский В.А., Попов Е.П. Теория систем автоматического регулирования, издание третье, исправленное. Москва, издательство «Наука», Главная редакция физико-математической литературы, 1975.

3. Гринченко А.Г. Теория автоматического управления: Учебн. пособие. – Харьков: ХГПУ, 2000. –272 с.

4. Зайцев Г.Ф. Теория автоматического управления и регулирования. – 2-е изд., перераб. и доп. Киев, Издательство Выща школа Головное издательство, 1989.

5. Справочник по теории автоматического управления. /Под ред. А.А. Красовского – М.: Наука, 1987. – 712 с.

6. Шандров Б.В. Технические средства автоматизации: учебник для студентов высших учебных заведений. Москва, Издательский центр «Академия», 2007.