Рівняння Максвела для Т, ТЕ, ТМ хвиль

Лекція 5

Рівняння Максвела для Т, ТЕ, ТМ хвиль.

Для однорідного ізотропного середовища в декартовій СК: .

Т - хвиля розповсюджується зі швидкістю світла, . Для неї . Підставимо в рівняння Максвела: ;

оскільки 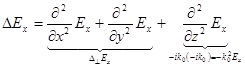, таким чином для Т – хвилі: - рівняння Лапласа. Для ТЕ та ТМ: , (хвиля розповсюджується в напрямку ). .

Маємо - для ТЕ, ТМ.

Ми отримали систему рівнянь Максвела:

.

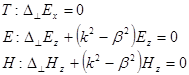
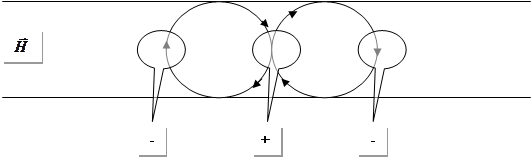
Т – хвиля існує там, де є розв’язок рівняння Лапласа (електрика). Ми знаємо, що рівнянням Лапласа описується електростатичне поле, наприклад у конденсаторі. Тому якщо існує електростатичне поле, то може існувати і Т – хвиля. Таким чином вона може існувати у конденсаторі, коаксіальному кабелі.

Оскільки одне рівняння і однакові граничні умови для електростатичного поля і Т – хвиля, то їх силові лінії співпадають.

Для того, щоб розв’язати задачу про хвилю, треба знайти:

1. Картину полів;

2. Сталу розповсюдження (швидкість);

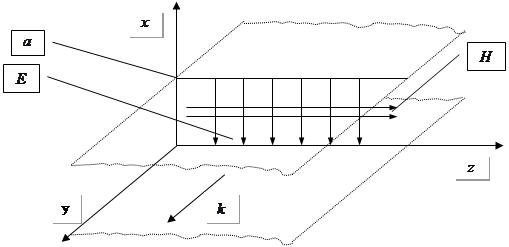Знайдемо ЕМ – поля між ║ пластинами:

Тут може існувати Т – хвиля, бо існує розв’язок рівняння Лапласа для конденсатора. Картина полів зображена на малюнку, таким чином ми розв’язали задачу без викладок. А чи може у цій системі розповсюджуватися Е чи Н хвиля? Для того щоб відповісти на це запитання, необхідно розв’язати задачу (розрахувати картину полів і знайти ):

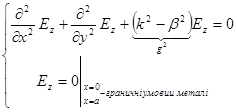, будемо вважати, що . Ми отримали задачу Коші: 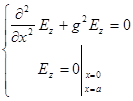. Її розв’язок . ; .

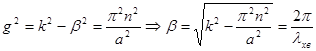. . Де - довжина хвилі у хвилі у хвилеводі.

Очевидно, що при ; тобто існує деяка критична довжина хвилі - така, що при хвиля не буде розповсюджуватися у хвилеводі: при : - уявне, тобто присутнє затухання.

; нижня .

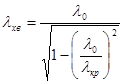Таким чином у хвилевід зайде Т – хвиля з будь-яким і Е – хвиля лише з . Можна отримати, що.Якщо зменшувати , то збільшується. Також змінюється при зміні . Існує критична частота, коли , тоді хвиля не розповсюджується. - довжина Т – хвилі у вільному просторі , ;

Таким чином, в результаті розв’язку рівняння Максвела ми знайшли лише одну компоненту хвилі . Однак для побудови картини необхідно знайти всі інші компоненти (у ТЕ та ТМ хвиль може бути не більше п’яти компонент). Скористаємося рівняннями Максвела: будемо виходити з .

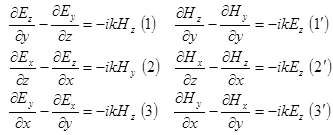
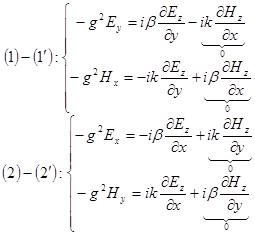Аналогічно для , таким чином, для неоднорідної хвилі ми отримали повний розв’язок: . Розглянемо пари: . В нашій Е – хвилі обов’язково , тоді з системи легко отримати інші компоненти: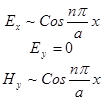. Таким чином маємо картину полів ТМ (Е – хвилі). Для ТЕ – хвилі – аналогічно.