Название: Класифікація електромагнітних явищ

Вид работы: реферат

Рубрика: Астрономия

Размер файла: 73.17 Kb

Скачать файл: referat.me-4564.docx

Краткое описание работы: Лекція 2 Класифікація електромагнітних явищ Існують загальні підходи для спрощення: Рівняння стаціонарного електромагнітного поля . Інколи можна розглядати постійні струми. При цьому в рівнянні (*) зникають похідні:

Класифікація електромагнітних явищ

Лекція 2

Класифікація електромагнітних явищ

Існують загальні підходи для спрощення:

1. Рівняння стаціонарного електромагнітного поля . Інколи можна розглядати постійні струми. При цьому в рівнянні (*) зникають похідні: 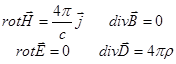Приклад використання: розрахунок наводок .

2. Розглянемо систему рівнянь у вакуумі , де . Рівняння магнітостатики: 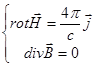, рівняння електростатики: 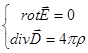. Рівняння магнітостатики має місце і там, де .Рівняння Максвела нехвильове. Хвильовим воно стає в однорідному ізотропному середовищі. Звідси тобто звідки одержуємо рівняння Лапласа : (з урахуванням заряду), Пуасона : (без).

3. Квазістатичне наближення : , - розмір об’єкту. Тоді рівняння Максвела спрощуються. Розглянемо метал: там просторові переходи дуже швидко зростають (швидке затухання) тобто частинними похідними можна знехтувати.

4. Для монохроматичного лінійного поля можна використати метод комплексних амплітуд : позбавляємося частинних похідних тобто спрощуємо рівняння Максвела. Рівняння ЕМП в комплексній формі будемо розглядати лише для лінійних рівнянь, хоча існує метод і для нелінійних. Розглянемо рівняння: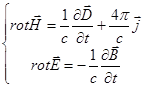. Зробимо наступну заміну:, та аналогічно . Підставивши отримаємо: , прирівнявши коефіцієнти отримуємо: 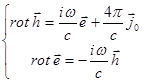- ми спростили рівняння. Для того, щоб записати лінійне ДР у комплексних амплітудах, потрібно: а) замість дійсних змінних записати комплексні змінні; б) замість похідних по часу треба записати . Для того щоб знайти розв’язок рівняння, потрібно розв’язати спрощене рівняння, а потім знайти реальну частину від одного з виразів: або . Часто рівняння записують з урахуванням того, що хвильовий вектор , де . Надалі ми будемо працювати в комплексних амплітудах.

Було б зручно звести рівняння Максвела до хвильових, але це можна зробити лише у деяких випадках, які і розглянемо.

Плоскі хвилі

Розглядатимемо плоскі хвилі в однорідному ізотропному середовищі.

Задача: знайти характеристики плоскої хвилі в такому середовищі.

Розв’язок:

1. Обираємо декартову систему координат;

2. Рівняння Максвела: ; де . У плоскої хвилі на хвильовому фронті амплітуда і фаза однакова. Нехай хвиля розповсюджується в напрямку , то . Отримаємо (з ). Розв’язок отриманог рівнянння осцилятора: .

Перейдемо до справжньої компоненти поля: де - рівняння хвильового фронту (фаза ). Цей фронт розповсюджується зліва направо. Якби ми взяли замість компоненту , то одержали б - фронт, що рухається справа наліво.

Розглянемо .

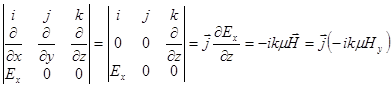. ; , тобто маємо дійсно праву трійку . Оскільки , то .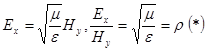

Таким чином у плоскій хвилі і залежні величини: якщо одне з них задане, то друге визначається лише серидовищем (див. *). Це в СГСЕ, в інших системах по іншому. Наприклад, в СІ у вакуумі 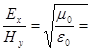377 (Ом) – опір вільного простору (хвильовий опір простору).

Затухання електромагнітних хвиль (ЕМХ).

Нехай вздовж осі розповсюджується ЕМХ: ; тут . Розглянемо в середовищі, де , (найрозповсюдженіший випадок); . Тоді . З’явилася дійсна величина в експоненті. Тобто кожна хвиля затухає.