Название: Структура и качество оптического изображения

Вид работы: реферат

Рубрика: Коммуникации и связь

Размер файла: 231.49 Kb

Скачать файл: referat.me-168358.docx

Краткое описание работы: БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ Кафедра ЭТТ РЕФЕРАТ На тему: «Структура и качество оптического изображения»

Структура и качество оптического изображения

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

Кафедра ЭТТ

РЕФЕРАТ

На тему:

«Структура и качество оптического изображения»

МИНСК, 2008

Основные характеристики структуры изображения

Изображающие приборы могут давать изображение различного качества с точки зрения передачи структуры предмета. Структура и форма светового поля в пространстве изображений подобна структуре и форме предмета, однако оптическая система вносит в эту структуру свои изменения, оценка которых есть оценка качества изображения.

Передача структуры предмета или изображения – это отображение оптической системой мелких деталей объекта. Для описания такого отображения необходимо математическое описание предмета и изображения в виде функций и . Эти функции описывают зависимость распределения интенсивности от пространственных координат.

Представим предмет в виде совокупности бесконечного количества светящихся точек. Для того, чтобы считать, что изображение предмета – это совокупность изображений соответствующих точек предмета, оптическая система должна удовлетворять свойствам линейности и инвариантности к сдвигу.

Свойство линейности

Изображение суммы объектов равно сумме изображений каждого объекта:

. (1)

То есть, если предмет – это сумма точек , то изображение – сумма изображений этих точек . Изображающие оптические системы полностью линейны.

Свойство инвариантности к сдвигу (условие изопланатизма)

При смещении точки ее изображение только смещается на пропорциональную величину (рис.1):

, (2)

где V – обобщенное увеличение.

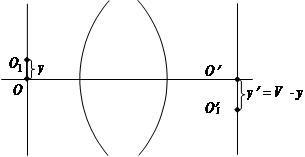
Рисунок.1 - Условие изопланатизма.

В отличие от условия линейности, условие изопланатизма в оптических системах соблюдается приблизительно, поскольку характер изображения при смещении изменяется. Изопланатизм, как правило, не соблюдается в пределах всего поля, обычно он соблюдается только при небольших смещениях.

Изопланатическая зона – это зона, в пределах которой соблюдается условие изопланатизма. Чем больше размер изопланатической зоны, тем лучше изопланатизм. Если зона полностью перекрывает предмет, то система полностью изопланатична. Мы будем рассматривать структуру изображения в пределах одной изопланатической зоны.

Функция рассеяния точки

В идеальной оптической системе точка изображается в виде точки, а в реальной оптической системе точка изображается в виде пятна рассеяния (рис.2).

Рисунок 2 - Изображение точки в пределах изопланатической зоны.

Основной характеристикой, описывающей передачу структуры предмета оптической системой является функция рассеяния точки .

Функция рассеяния точки (ФРТ, point spread function, PSF) – это функция, описывающая зависимость распределения освещенности от координат в плоскости изображения, если предмет – это светящаяся точка в центре изопланатической зоны.

Зная функцию рассеяния точки, можно найти изображение любого предмета, если разложить его на точки и найти ФРТ от каждой точки. Если есть предмет , то каждая его точка изображается в виде функции , то есть ФРТ смещается в точку с координатами (рис.2), а изображение всего предмета будет представлять собой сумму этих изображений:

. (3)

Если увеличение V принять за единицу, то выражение (3) становится сверткой (конволюцией).

Функция изображения есть свертка функции предмета с функцией рассеяния точки:

(4)

Гармонический периодический объект

Предмет кроме разложения на отдельные точки можно разложить на другие элементарные части – периодические решетки.

Периодическая решетка – это структура с белыми и черными полосами.

Гармоническая периодическая решетка – это структура, интенсивность которой описывается гармонической функцией (рис.3).

В электронике существует аналог гармонической решетки – периодический во времени сигнал на входе прибора.

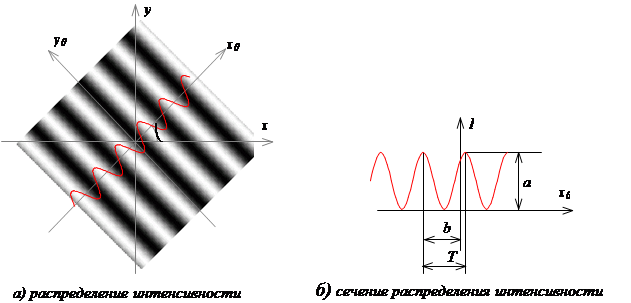
Рисунок 3 - Гармоническая периодическая решетка

Гармоническая периодическая решетка описывается выражением:

, (5)

где a – вещественная амплитуда, b – сдвиг, T – период, q – угол ориентации.

Вместо периода можно использовать пространственную частоту , а вместо вещественной амплитуды и сдвига – комплексную амплитуду:

, (6)

Тогда интенсивность гармонической решетки в комплексной форме:

, (7)

Величину можно выразить как , тогда интенсивность гармонической решетки будет зависеть от двух координат ( x , y ):

(8)

где – частота в направлении x, – частота в направлении y.

Любой объект, как было сказано выше, можно разложить на элементарные гармонические объекты, тогда изображение – это совокупность изображений элементарных объектов. Эти изображения для реальных оптических систем всегда имеют искажения, что связано с законом сохранения энергии. Идеальные оптические системы нарушают закон сохранения энергии, так как они для сохранения неизменной структуры предмета должны передавать бесконечно большую энергию.

Изображение гармонического объекта можно описать, если в выражение (9.3) подставить в качестве распределения интенсивности на предмете функцию (8):

. (9)

Если выразить координаты предмета и изображения в едином масштабе, то V=1, следовательно:

.

После замены переменных получим:

или, после переобозначения :

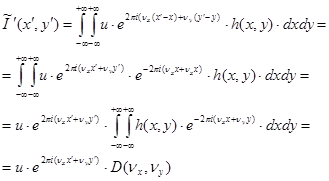. (10)

Двойной интеграл в выражении (9.10) – это некоторая функция , зависящая от пространственных частот.

Обозначим , и запишем распределение интенсивности на изображении гармонического объекта в следующем виде:

. (11)

Как показывают соотношения (8) и (11), изображение от предмета отличается только комплексной амплитудой, то есть изображение гармонической решетки любой оптической системы есть гармоническая решетка с той же частотой. Поэтому гармоническую решетку удобно использовать для исследования и оценки передачи структуры изображения. Изменение комплексной амплитуды гармонической решетки – это и есть действие оптической системы.

Оптическая передаточная функция (ОПФ)

Оптическая передаточная функция (optical transfer function, OTF) характеризует передачу структуры предмета оптической системой как функция пространственных частот:

. (12)

ОПФ связана с ФРТ интегральным преобразованием – преобразованием Фурье:

(13)

или

или ,

где F – обозначение Фурье преобразования:

. (14)

ФРТ показывает, как оптическая система изображает точку, а ОПФ показывает, как оптическая система изображает гармоническую решетку, то есть как меняется комплексная амплитуда решетки в зависимости от частоты.

Оптическая передаточная функция – это комплексная функция:

. (15)

Модуль ОПФ называется модуляционной передаточной функцией (МПФ) или частотно-контрастной характеристикой (ЧКХ). Аргумент (фаза) ОПФ называется фазовой передаточной функцией (ФПФ) или частотно-фазовой характеристикой (ЧФК).

Частотно-контрастная характеристика показывает передачу вещественной амплитуды гармонического объекта:

, (16)

где a – амплитуда на предмете, a¢ – амплитуда на изображении.

Амплитуда изображения гармонического объекта тесно связана с контрастом. Контраст для периодических (гармонических) изображений (рис.9.4) определяется выражением:

. (17)

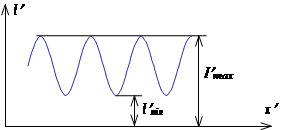
Рисунок 4 - Контраст гармонического объекта.

. Абсолютный контраст получается, когда (рис.5.а). Контраст в изображении нулевой , когда – изображение практически отсутствует (рис.5.б).

Рисунок 5 - Абсолютный и нулевой контраст гармонического объекта

Чем больше контраст, тем лучше различаются мелкие детали изображения. Изображение нельзя зарегистрировать или увидеть в случае, если:

, (18)

где – порог контраста, зависящий от приемника изображения (например, для глаза ).

Контраст для изображения гармонического объекта может быть выражен через постоянную a¢₀ и a¢ переменную составляющие изображения гармонического объекта (рис.6):

. (19)

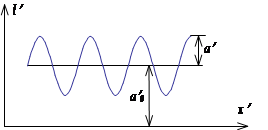
Рисунок 6 - Постоянная и переменная составляющие изображения гармонического объекта

Если , то ЧКХ, как следует из выражения (16) будет определяться следующим соотношением:

, (20)

где k¢ – контраст изображения, k – контраст предмета.

Частотно-контрастная характеристика показывает зависимость контраста изображения гармонической решетки от частоты решетки, если считать, что на предмете контраст единичный (рис.7). Для идеальной оптической системы ЧКХ – прямая, параллельная оси.

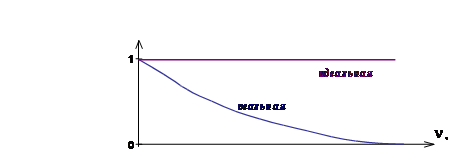
Рисунок 7 - Частотно-контрастная характеристика.

Для ближнего типа предмета или изображения пространственная частота n измеряется в [лин/мм]. Для дальнего типа пространственная частота измеряется в [лин/рад].

Итак, передача структуры изображения описывается ФРТ или ОПФ, которые связаны через взаимно однозначные преобразования Фурье. Наглядно отобразить двумерную функцию ОПФ можно в виде:

- графиков сечений или ,

- изометрического изображения “поверхности” ,

- карты уровней .

Схема формирования оптического изображения

Существует два фактора, которые влияют на структуру и качество изображения в оптической системе: дифракция и аберрации. Эти факторы действуют совместно. Если аберрации малы и преобладает дифракция, то такие системы называются дифракционно-ограниченными . Если аберрации велики, и дифракция теряется на фоне аберраций, то такие системы называются геометрически-ограниченными (формирование изображения вполне корректно описывается с позиций геометрической оптики, без привлечения теории дифракции).

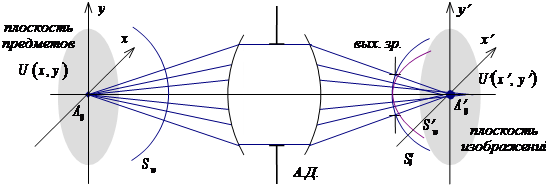
Рисунок 8 - Схема формирования оптического изображения.

Рассмотрим формирование изображения некоторой точки (рис.8). Гомоцентрический пучок лучей выходит из точки A₀ , и после идеальной оптической системы сходится в точке A¢₀ . Наряду с пучками лучей можно также рассматривать сферические волновые фронты S_w и S¢_w . Действие реальной оптической системы сводится к следующим факторам:

- преобразование расходящегося пучка лучей (волнового фронта) в сходящийся,

- ограничение размеров проходящего пучка лучей или волнового фронта,

- ослабление интенсивности (энергии) проходящего поля,

- нарушение гомоцентричности пучка или сферичности волнового фронта, то есть изменение фазы проходящего поля.

Рассмотрим поле на выходной сфере (в области выходного зрачка). Волновой фронт близок к выходной сфере, но отличается от нее на величину волновой аберрации. Поле на волновом фронте . Оптический путь из центра предмета до волнового фронта для всех лучей одинаковый, так как волновой фронт – поверхность равного эйконала. Поскольку для формирования изображения важна разность фаз между выходной сферой и волновым фронтом, а не сама фаза, то можно принять, что фаза волнового фронта равна нулю j=0. При отсутствии аберраций амплитуда поля единичная, следовательно поле на волновом фронте . Набег фазы от выходной сферы до волнового фронта:

, (21)

где – расстояние между волновым фронтом и выходной сферы вдоль луча.

Поле на выходной сфере математически можно представить в виде:

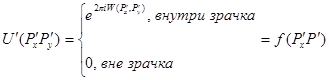, (22)

где – волновая аберрация, – зрачковая функция.

В выражении (22) учитывается одновременно ограничение пучков и наличие аберраций.

Зрачковая функция (pupil function, PF) показывает влияние оптической системы на прохождение электромагнитного поля от точки предмета до выходного зрачка и в общем случае в канонических координатах описывается выражением:

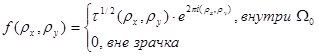, (23)

где – канонические зрачковые координаты, – функция пропускания по зрачку, – область зрачка в канонических координатах.

Теперь нужно перейти от поля на выходном зрачке к полю на изображении. Вблизи изображения геометрическая оптика не применима, поэтому для описания поля на изображении следует использовать теорию дифракции.

Рисунок 9 - Формирование комплексной амплитуды в плоскости изображения.

Для вычисления комплексной амплитуды поля в плоскости изображения применим принцип Гюйгенса в форме интеграла Гюйгенса-Френеля. Рассматриваемая область находится вблизи центра выходной сферы (рис. 9):

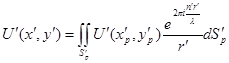. (23)

Используя зрачковую функцию, выражение (9.23) можно записать в виде:

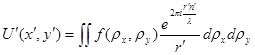. (24) Поскольку и, то множитель можно представить в виде . Множитель , следовательно его можно вынести за интеграл, и не учитывать, так как нас интересует только относительное распределение комплексной амплитуды. Тогда выражение (24) преобразуется так:

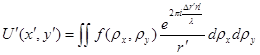(25)

можно выразить через и (рис. 10).

Рисунок 10 - Связь с радиусом выходной сферы и расстоянием

от выходной сферы до точки

Отрезок , причем – для крайнего луча, а для остальных лучей: , . Теперь интеграл (25) можно записать так:

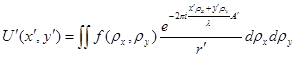. (26)

Введем канонические (приведенные) координаты на предмете и изображении:

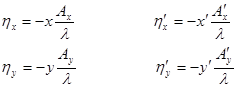. (27)

Тогда в канонических координатах получим:

. (28)

Так как зрачковая функция вне зрачка равна нулю, интегрирование происходит внутри зрачка. Комплексная амплитуда в изображении точки в канонических координатах, как следует из выражения (28), связана со зрачковой функцией через обратное преобразование Фурье:

. (29)

Комплексная амплитуда поля в изображении точки есть обратное Фурье-преобразование от зрачковой функции в канонических координатах.

Функция рассеяния точки – это распределение не амплитуды поля, а интенсивности, то есть квадрата модуля комплексной амплитуды . Тогда для ФРТ можно получить следующее выражение:

. (30)

Оптическую передаточную функцию также можно выразить в канонических координатах:

, (31)

где – канонические пространственные частоты :

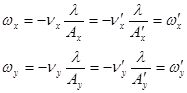(32)

Канонические частоты безразмерные: . В этих координатах получаем простую связь зрачковой функции с оптической передаточной функцией:

. (33)

Это выражение в соответствии со свойством преобразования Фурье можно представить через автокорреляцию зрачковой функции:

, (34)

где – площадь зрачка в канонических координатах.

ЛИТЕРАТУРА

1. Бегунов Б.Н., Заказнов Н.П. и др. Теория оптических систем. – М.: Машиностроение, 2004

2. Дубовик А.С. Прикладная оптика. – М.: Недра, 2002

3. Нагибина И.М. и др. Прикладная физическая оптика. Учебное пособие.- М.: Высшая школа, 2002