Название: Теорема Котельникова. Побудова ортонормованого базису

Вид работы: контрольная работа

Рубрика: Коммуникации и связь

Размер файла: 86.12 Kb

Скачать файл: referat.me-168862.docx

Краткое описание работы: Зміст теореми Найквіста-Шенона. Задача на визначення сигналу, відновленого за допомогою фільтрації. Схема включення ФНЧ. Балансна амплітудна модуляція. Однотональний Ам-сигнал з балансною модуляцією. Аналітичний сигнал обвідної заданого коливання.

Теорема Котельникова. Побудова ортонормованого базису

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

ЧЕРКАСЬКИЙ ДЕРЖАВНИЙ ТЕХНОЛОГІЧНИЙ УНІВЕРСИТЕТ

Кафедра радіотехніки

КОНТРОЛЬНА РОБОТА

з курсу «Сигнали та процеси»

Варіант № 9

Черкаси 2010

Варіант 9

1. Теорема Котельникова. Побудова ортонормованого базису

Теорема Котельникова (у англомовній літературі - теорема Найквіста - Шенона ) свідчить, що, якщо аналоговий сигнал має обмежений спектр, то він може бути відновлений однозначно і без втрат по своїх дискретних відліках, узятих з частотою більш подвоєної максимальної частоти спектру :

де - верхня частота в спектрі, або (формулюючи по-іншому) по відліках, узятих з періодом , частіше за напівперіод максимальної частоти спектру

Пояснення:

Таке трактування розглядає ідеальний випадок, коли сигнал почався нескінченно давно і ніколи не закінчиться, а також не має в тимчасовій характеристиці точок розриву. Саме це має на увазі поняття «спектр, обмежений частотою ».

Зрозуміло, реальні сигнали (наприклад, звук на цифровому носієві) не володіють такими властивостями, оскільки вони кінцеві за часом і, зазвичай, мають в тимчасовій характеристиці розриви. Відповідно, їх спектр безконечний. В такому разі повне відновлення сигналу неможливе і з теореми Котельникова витікають 2 слідства:

1. Будь-який аналоговий сигнал може бути відновлений з якою завгодно точністю по своїх дискретних відліках, узятих з частотою

де - максимальна частота, якою обмежений спектр реального сигналу.

2. Якщо максимальна частота в сигналі перевищує половину частоти переривання, то способи відновити сигнал з дискретного в аналоговий без спотворень не існує.

Кажучи ширше, теорема Котельникова стверджує, що безперервний сигнал можна представити у вигляді інтерполяційного ряду

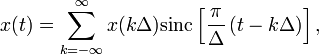
де - Інтервал дискретизації задовольняє обмеженням Миттєві значення даного ряду є дискретні відліки сигналу .

Згодом було запропоновано велике число різних способів апроксимації сигналів з обмеженим спектром, узагальнювальних теорему відліків. Так, замість кардинального ряду по sinc-функціям, що є характеристичними функціями прямокутних імпульсів, можна використовувати ряди по конечно або бесконечнократним сверткам sinc-функцій.

Наприклад, справедливо наступне узагальнення ряду Котельникова безперервної функції з фінітним спектром на основі перетворень Фур'є атомарних функцій:

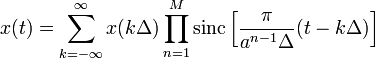
де параметри задовольняють нерівності , а інтервал дискретизації

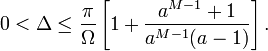
2. З неперервного сигналу s(t) = 10cos(2π800t)В беруться ідеальні відліки з частотою f_В = 400Гц. Отримані дискретні сигнали пропускаються через ідеальний ФНЧ з частотою зрізу 0,4f_В . Необхідно визначити сигнал, відновлений за допомогою фільтрації

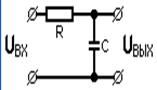
Схема включення ФНЧ (рис. 1).

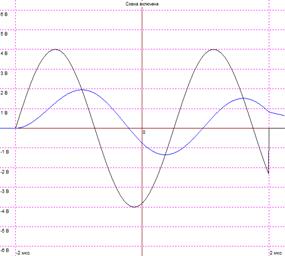
Рисунок 1 - Сигнал s(t) = 10cos(2π800t) В

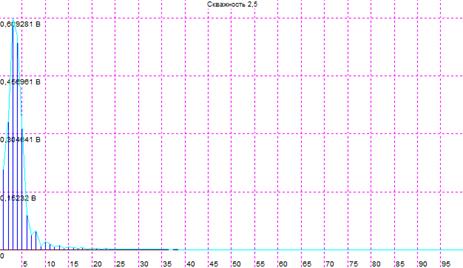
Рисунок 2 – Гармоніка

3. Балансна амплітудна модуляція

У амплітудно-модульованому (АМ) сигналі:

значна доля потужності зосереджена в несучому коливанні

Для ефективнішого використання потужності передавача можна формувати Ам-сигнали з пригніченим несучим коливанням, реалізовуючи так звану балансну амплітудну модуляцію (рис. 3).

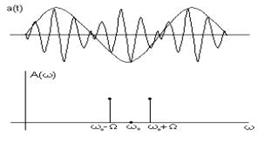
Рис. 3

Однотональний Ам-сигнал з балансною модуляцією має вигляд:

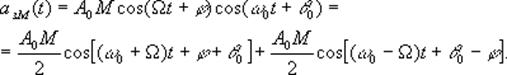
Такий сигнал з фізичної точки зору є биттям двох гармонійних сигналів з однаковими амплітудами і частотами і Під час переходу тієї, що огинає биття через нуль фаза високочастотного заповнення стрибком змінюється на 180^о , оскільки функція має різні знаки справа і зліва від нуля. Здійснення балансної модуляції, як і зворотного процесу демодуляції (детектування), технічно складніше, ніж при звичайній амплітудній модуляції.

4. Задані параметри коливання з односмуговою АМ: А₀ = 25 В, Е = 1,5 В, θ₀ = π/4, γ = π/3, f₀ = 20 кГц, F = 4 кГц. Записати вираз для аналітичного сигналу і комплексної обвідної заданого коливання

u_Ω (t)= U_Ω sinΩt

u(t) = U_ω sinω₀ t + m U_ω /2 sin(ω₀ + Ω) t+ m U_ω /2 sin(ω₀ - Ω) t

u(t) = (U_ω + U_Ω sinΩt) sinω₀ t

u(t) = (А₀ + Е sin(f₀ t+ θ₀ ) )sin (F t + γ ) =(25 + 1,5 sin(20 t + π/4) )sin (2 t + π/3).