Referat.me
/ / Комбинированый метод для вычисления корня уравнения

Название: Комбинированый метод для вычисления корня уравнения

Вид работы: реферат

Рубрика: Коммуникации и связь

Размер файла: 105.02 Kb

Скачать файл: referat.me-169376.docx

Краткое описание работы: Цель работы: Изучить комбинированный метод для вычисления действительного корня уравнения, уметь использовать данный метод для решения уравнений с использованием ЭВМ.

Комбинированый метод для вычисления корня уравнения

2.1 Цель работы:

Изучить комбинированный метод для вычисления действительного корня уравнения, уметь использовать данный метод для решения уравнений с использованием ЭВМ.

2.2 Расчётные формулы

Расчётная формула вычисления -го приближения по методу касательных:

.

Расчётная формула вычисления -го приближения по методу хорд:

.

Начальное приближение для метода касательных выбирают в соответствии с условием:

, если ,

или , если .

Начальное приближение для метода хорд тогда принимается , или соответственно.

Процесс вычисления корня останавливается, когда выполняется условие:

,

где – заданная точность.

За приближенное значение корня уравнения принимается:

.

2.3 Подготовительная работа

Вычислить корень уравнения с точность комбинированным методом.

Графически отделим корни. Для этого данное уравнение запишем в виде . Строим графики функций и (рис. 2.1).

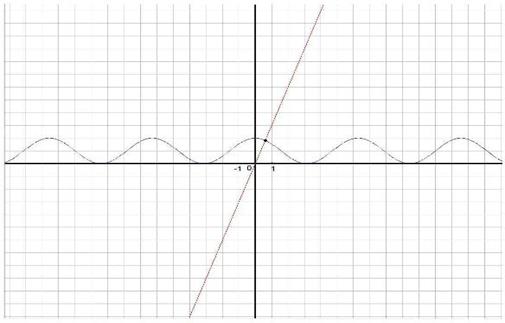
Рисунок 2.1

Точный корень уравнения , отрезок [0;1] – интервал изоляции корня.

Проверяем условия, гарантирующие единственность корня на [0;1] и сходимость метода:

непрерывна на [0;1] и не меняет знак:.

непрерывна на [0;1] и не меняет знак:.

За начальное приближение для метода касательных берём , для метода хорд .

Процесс вычисления корня:

.

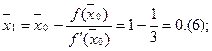
Условие не выполняется, процесс вычисления корня продолжается до достижения заданной точности .

Требуемая точность вычисления результата была достигнута за 2 итерации. Результат 0,607199.

2.4 Текст программной реализации

#include <iostream>

#include <math.h>

using namespace std;

double f(double x)

{

return 3*x-cos(x)-1;

}

double fw(double x)

{

return 3+sin(x);

}

void main()

{

double xk, xh, tochnost, otvet;

cout<<"Vvedite nachalnoe priblizhenie po metodu kasatelnih xk=";

cin>>xk;

cout<<"nVvedite nachalnoe priblizhenie po metodu hord xh=";

cin>>xh;

cout<<"nX-hordttX-kasatelnihtTochnostn-----------------------------------";

int n;

for(n=0; n<20; n++)

{

xh -= f(xh)*(xk-xh)/(f(xk)-f(xh));

xk -= f(xk)/fw(xk);

tochnost=fabs(xh-xk);

cout<<'n'<<xh<<'t'<<xk<<'t'<<tochnost;

if(tochnost<0.001) break;

};

n++;

otvet=(xh+xk)/2;

cout<<"nnKolichestvo iteraciy="<<n;

cout<<'n'<<'n'<<"Koren uravneniya="<<otvet;

cin>>xk;

}

Похожие работы

  • Расчет частотных характеристик активного фильтра второго порядка на операционном усилителе

    МО УКРАИНЫ Севастопольский государственный технический университет Кафедра РЭ КУРСОВАЯ РАБОТА по дисциплине «Основы автоматизации проектирования радиоэлектронной аппаратуры»

  • Методы расчета линейных электрических цепей при импульсном воздействии. Спектральный анализ сигналов

    Выполнение качественного анализа переходных процессов напряжений и токов на реактивных элементах, их расчет классическим и операторным методами. Вычисление и построение графика спектральной плотности амплитуд прямоугольного импульса и искомой переменной.

  • Исследование переходных процессов

    Расчеты переходных процессов в линейных электрических цепях со сосредоточенными параметрами и определение искомого напряжения на отдельном элементе схемы классическим и операторным методом. Построение графика в имитационном режиме WorkBench по этапам.

  • Устойчивость дискретных систем управления

    Основные понятия устойчивости дискретных систем. Критерий устойчивости Михайлова с использованием билинейного преобразования. Определение устойчивости дискретных систем в форме z-преобразования. Применение критериев устойчивости для дискретных систем.

  • Разработка математической модели электронного устройства

    Расчет переходного процесса на основе численных методов решения дифференциальных уравнений. Разработка математической модели и решение с использованием метода пространства состояний. Составление математической модели с помощью матрично-векторного метода.

  • Теория информационных процессов

    Система автоматического управления. Алгоритм модального формирования динамических свойств системы. Матрица линейных стационарных обратных связей на основе алгебраического уравнения типа Сильвестра. Математическая модель наблюдателя Люенбергера.

  • Теория автоматического управления

    Анализ устойчивости замкнутой системы по корням характеристического уравнения, алгебраическому и частотному критерию. Построение области устойчивости в плоскости параметра Кр. Методы коррекции исследуемой системы. Построение и анализ ЛЧХ системы.

  • Расчет жесткого стержня

    Построение математической модели и составление программы для расчета опорных реакций жесткого стержня с тремя опорными узлами. Определение внутренних усилий, поперечной силы Q и изгибающего момента М во внутренних сечениях стержня под действием нагрузки.

  • Анализ устойчивости электротехнической системы

    Возможности математического пакета MathCad. Использование алгебраического критерия Рауса-Гурвица для анализа устойчивости систем. Построение годографов Найквиста по передаточной функции разомкнутой системы заданной в виде полинома, использование ЛАХЧ.

  • Расчёт переходных процессов в линейных электрических цепях с сосредоточенными параметрами

    Суть классического метода расчёта для мгновенных значений всех токов цепи и напряжений на реактивных элементах после коммутации. Операторный метод расчёта для тока в катушке индуктивности, принцип действия синусоидального закона в переходном процессе.