Referat.me / Логика / Методика расчета развозочных маршрутов

Название: Методика расчета развозочных маршрутов

Вид работы: контрольная работа

Рубрика: Логика

Размер файла: 102.58 Kb

Скачать файл: referat.me-204228.docx

Краткое описание работы: МЕЖДУНАРОДНЫЙ СЛАВЯНСКИЙ ИНСТИТУТ НИЖЕГОРОДСКИЙ ФИЛИАЛ Контрольная работа по логистике Выполнила: Студентка гр. ФВ 64 Жердова О.В. Проверил: Д.т.н., профессор

Методика расчета развозочных маршрутов

МЕЖДУНАРОДНЫЙ СЛАВЯНСКИЙ ИНСТИТУТ

НИЖЕГОРОДСКИЙ ФИЛИАЛ

Контрольная работа

по логистике

Выполнила:

Студентка гр. ФВ 64

Жердова О.В.

Проверил:

Д.т.н., профессор

Федоров О.В.

2010 г.

Методика расчета развозочных маршрутов. Потребность в мелкопартионных поставках продукции потребителям с баз и складов систематически возрастает. Поэтому организация маршрутов на отгрузку потребителям мелких партий груза имеет большое значение.

Введем обозначения:

x_i – пункты потребления ( i=1,2 … n);

x_o – начальный пункт (склад);

q – потребность пунктов потребления в единицах объема груза;

Q_d – грузоподъемность транспортных средств;

d– количество транспортных средств;

C_ij – стоимость перевозки (расстояние);

j- поставщики (j = 1,2 … M).

Имеются пункты потребления x_i (i=1,2 … n). Груз необходимо развести из начального пункта x_o (склад) во все остальные (потребители). Потребность пунктов потребления в единицах объема груза составляет: q_1, q_2, q_{3 …} q_n _.

В начальном пункте имеются транспортные средства грузоподъемностью Q₁ , Q₂ … Qd.

При этом d > nв пункте x_o количество груза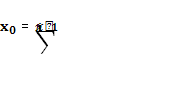

, каждый пункт потребления снабжается одним типом подвижного состава.

Для каждой пары пунктов (x_i , x_j ) определяется стоимость перевозки (расстояние) C_ij > 0, причем матрица стоимостей в общем случае может быть ассиметричная, т. е. C_ij C_ij .

Требуется найти mзамкнутых путей l₁ , l₂ , … l_m из единственной общей точки x_o , так чтобы выполнялось условие

Методика составления рациональных маршрутов при расчетах вручную.

2,2 7,0

5,0

4,23,2

4,4 3,6 5,6

2,4 1,9 2,0 5,0

2,0 3,4 5,8

2,8

2,6

Рис. 1.Схема размещения пунктов и расстояния между ними

Потребители продукции	Б	В	Г	Д	Е	Ж	З	И	К
Объем продукции, кг	375,0	500	500	300	425	525	575	675	125

Груз находится в пункте А - 4000 кг. Используется автомобиль грузоподъемность 2,5 т; груз – IIкласса (ᵧ = 0,8). Необходимо организовать перевозку между пунктами с минимальным пробегом подвижного состава.

Решение состоит из нескольких этапов:

Этап 1. Строим кратчайшую сеть, связывающую все пункты без замкнутых контуров.

4000 кг

375 кг

3,2 км

2,2 км

500 кг

2,0 км

3,6 км

300 кг

425 кг 5,0 км

525 кг

2,4 км 2,8 кг

125 кг

2,0 км 2,6 км

575 кг 675 кг

Рис. 2. Кратчайшая связывающая сеть («минимальное дерево»)

Затем по каждой ветви сети, начиная с пункта, наиболее удаленного от начального А (считается по кратчайшей связывающей сети), группируем пункты по маршруту с учетом количества ввозимого груза и грузоподъемности единицы подвижного состава. Причем ближайшие с другой ветви пункты группируем вместе с пунктами данной сети.

Исходя из заданной грузоподъемности подвижного состава Q=2,5, ᵧ = 0,8 все пункты можно сгруппировать так:

Маршрут I		Маршрут II
пункт	объем завоза, кг	пункт	объем завоза, кг
Б	375	Ж	525
В	500	Д	300
Е	425	И	675
З	575	Г	500
К	125
итого	2000	итого	2000

Сгруппировав пункты по маршрутам, переходим ко второму этапу расчетов.

Этап II. Определяем рациональный порядок объезда пунктов каждого маршрута. Для этого строим таблицу-матрицу, в которой по диагонали размещаем пункты, включаемые в маршрут, и начальный пункт А, а в соответствующих клетках – кратчайшее расстояние между ними. Для примера матрица является симметричной C_ij C_ij , хотя приведенный ниже способ применим для размещения несимметричных матриц.

А	7,0	9,2	9,0	11,4	10,6
7,0	Б	2,2	4,2	6,6	7,6
9,2	2,2	В	3,6	4,4	6,4
9,0	4,2	3,6	Е	2,4	3,4
11,4	6,6	4,4	2,4	З	2,0
10,6	7,6	6,4	3,4	2,0	К
∑ 47,2	27,6	25,8	22,6	26,0	30,0

Начальный маршрут строим из трех пунктов матрицы АКБА, имеющих наибольшее значение величины, показанных в строке (47,2; 30,0; 27,6), т.е. А; К; Б. Для включения последующих пунктов выбираем из оставшихся пункт,имеющий наибольшую сумму, например З (сумма 25,8), и решаем, между какими пунктами его следует включать, т.е. между А и К, К и Б или Б и А.

Поэтому для каждой пары пунктов необходимо найти величину приращения маршрута по формуле:

kp = Ck_i + C_i p – Ckp,

где С – расстояние, км; i – индекс включаемого пункта; k – индекс первого пункта из пары; p – индекс второго пункта из пары.

При включении пункта З между первой парой пунктов А и К определяем размер приращения ∆АК при условии, что i = 3, k = А, p = К. Тогда

∆АК = С_АЗ + С_ЗК - С_АК

Подставляя значения из таблицы на стр. 5, получаем, что

∆АК = 11,4 + 2,0 – 10,6 = 2,8

Таким же образом определяем размер приращения ∆КБ, если З включим между пунктами К и Б:

∆КБ = С_КЗ + С_ЗБ – С_КБ = 2,0 + 6,6 – 7,6 = 1,0 км,

∆БА, если З включить между пунктами Б и А:

∆БА = С_БЗ + С_ЗА – С_АБ = 6,0 + 11,4 – 7,0 = 11,0 км

Из полученных значений выбираем минимальное, т. е. ∆КБ= 1,0. Тогда из А-К-Б-А→А-К-З-Б-А. Используя этот метод и формулу приращения, определяем, между какими пунктами расположить пункты В и Е. Начнем с В, так как размер суммы (см. табл. на с. 5) этого пункта больше (27,6 > 22,6):

∆АК = С_АБ + С_ВК – С_АК = 9,2 + 6,4 – 10,6 = 5,0,

∆КЗ = С_КВ + С_ВЗ – С_КЗ = 6,4 +4,4 – 2,0 = 8,8,

∆ЗБ = С_ЗВ + С_ВБ – С_ЗБ = 4,4 + 2,2 – 6,6 = 0.

В случае, когда ∆ = 0, для симметричной матрицы расчеты можно не продолжать, так как меньше значение чем 0 получено быть не может. Поэтому пункт В должен быть между пунктами З и Б. Тогда маршрут получит вид: А – К – З – В – Б - А.

В результате проведенного расчета включаем пункт Е между пунктами З и В, так как для этих пунктов мы получим минимальное приращение 1,6:

∆АК = С_АЕ + С_ЕК – С_АК = 9,0 + 3,4 – 10,6 = 1,8;

∆КЗ = С_{КЕ +} С_ЕЗ – С_КЗ = 3,4 + 2,4 – 2,0 = 3,9;

∆ЗВ = С_ЗЕ + С_ЕВ – С_ЗВ = 2,4 + 3,6 – 4,4 = 1,6;

∆ВБ = С_ВЕ + С_ЕБ – С_ВБ = 3,6 + 4,2 – 2,2 = 5,4;

∆БА = С_БЕ + С_ЕА – С_БА = 4,2 + 9,0 – 7,0 = 6,1.

Таким образом, окончательный порядок движения по маршруту Iбудет А – К – З – Е – В – Б – А.

Таким же методом определим кратчайший путь объезда пунктов по маршруту II. В результате расчетов получим маршрут А – Г – Д – И – Ж – А длиной 19,4 км. Порядок движения по маршрутам Iи II приведен на рис.3.

7,0