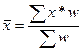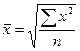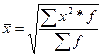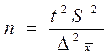Название: Группировка статистических данных и ее роль в анализе информации
Вид работы: реферат
Рубрика: Менеджмент
Размер файла: 293.84 Kb
Скачать файл: referat.me-242494.docx
Краткое описание работы: Содержание Семестр 1_ 2 Группировка статистических данных и ее роль в анализе информации_ 2 Абсолютные, относительные, средние величины_ 2 Относительные величины_ 2
Группировка статистических данных и ее роль в анализе информации
Содержание
Семестр 1_ 2
Группировка статистических данных и ее роль в анализе информации_ 2
Абсолютные, относительные, средние величины_ 2
Относительные величины_ 2
Средние величины_ 2
Статистические распределения и их характеристики_ 3
Показатели вариации (колеблемости) признака_ 4
Сложение дисперсий_ 4
Показатель асимметрии_ 5
Показатель эксцесса (островершинности) 5
Кривые распределения 5
Выборочное наблюдение 6
Формулы ошибок простой случайной выборки_ 7
Формулы для определения численности простой и случайной выборки_ 7
Типичная выборка_ 7
Серийная выборка_ 8
Малые выборки_ 8
Корреляционная связь_ 8
Уравнение регрессии_ 9
Ряды динамики_ 10
Показатели динамики_ 10
Средние показатели динамики_ 10
Тренды_ 11
Семестр 2 (Индексы) 11
Семестр 1
Группировка статистических данных и ее роль в анализе информации
Равный интервал
, величина интервала - ![]() , m
– число групп
, m
– число групп
Формула Стерджесса (величина интервала) - ![]() , n
– число наблюдений
, n
– число наблюдений
Абсолютные, относительные, средние величины
Относительные величины
Относительные величины (ОВ) динамики характеризуют изменение явления во времени. (Коэффициент роста)
Темп роста
– с переменной базой - ![]() yn
– уровень явления за период
(например, выпуск продукции по кварталам года)
yn
– уровень явления за период
(например, выпуск продукции по кварталам года)
С постоянной базой - ![]() , yk
– постоянная база сравнения
, yk
– постоянная база сравнения
ОВ планового задания
- ![]()
ОВ выполнения плана
- ![]()
ОВ динамики
- ![]()
ОВ структуры
характеризуют долю отдельных частей в общем объеме совокупности (удельный вес) - ![]()
ОВ координации отражают отношение численности двух частей единого целого, т. е. показывают, сколько единиц одной группы приходится в среднем на одну, на 10 или на 100 единиц другой изучаемой совокупности.
ОВ координации - ![]()
ОВ наглядности (сравнения) отражают результаты сопоставления одноименных показателей, относящихся к одному и тому же периоду времени, но к разным объектам или территориям (например, сравнивается годовая производительность труда по 2-м предприятиям)
ОВ сравнения - ![]()
Средние величины
Степенные средние общего типового расчета:
Средняя степенная простая
- 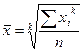 ,
, ![]() - индивидуальное значение признака, по которому рассчитывается средняя,
n
– объем совокупности (число единиц)
- индивидуальное значение признака, по которому рассчитывается средняя,
n
– объем совокупности (число единиц)
Средняя степенная взвешенная
- 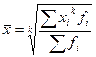 , fi
– частота повторения индивидуального признака
(
, fi
– частота повторения индивидуального признака
(![]() =n)
=n)
| Значе-ние k |
Наименование средней |
Формула средней |
|
| Простая |
Средняя |
||
| -1 |
Гармоническая |
|
|
| 0 |
Геометрическая |
|
|
| 1 |
Арифметическая |
|
|
| 2 |
Квадратическая |
|
|
![]() гарм.
<
гарм.
< ![]() геом
<
геом
< ![]() арифм
<
арифм
< ![]() квадрат
, x=w/f
квадрат
, x=w/f
Гармоническая простая – когда небольшая совокупность и индивидуальные значения не повторяются. Используется, если исчисляем среднюю из обратных величин.
Средняя квадратическая – для расчета среднего квадратического отклонения, являющегося показателем вариации признаков
Средняя геометрическая простая – для вычисления среднего коэффициента роста (темпа) в рядах динамики, если промежутки, к которым относятся коэффициенты роста, одинаковы.
Статистические распределения и их характеристики
Мода – значение признака, которое наиболее часто встречается в совокупности
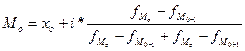 ,
, ![]() - нижняя граница модального интервала (интервал с наибольшей частотой),
- нижняя граница модального интервала (интервал с наибольшей частотой), ![]() - величина интервала,
- величина интервала, ![]() - частота в модальном интервале.
- частота в модальном интервале.
Медиана – значение признака, которое лежит в середине ранжированного ряда и делит этот ряд на две равные по численности части.
![]() - положение медианы
- положение медианы
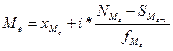 ,
, ![]() - нижняя граница медианного интервала,
- нижняя граница медианного интервала, ![]() - накопленная частота интервала, предшествующего медианному,
- накопленная частота интервала, предшествующего медианному, ![]() - частота медианного интервала.
- частота медианного интервала.
Квартель
![]() ,
, ![]()
![]() ,
, ![]()
Дециль
![]() ,
, ![]() (от 1/10 до 9/10)
(от 1/10 до 9/10)
Показатели вариации (колеблемости) признака
Среднее линейное отклонение – на сколько в среднем отличаются индивидуальные значения признака от среднего его значения.
-для несгруппированных данных (первичного ряда): ![]()
-для вариационного ряда: 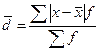
Среднее квадратическое отклонение
- для несгруппированных данных: 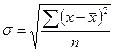
- для вариационного ряда: 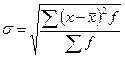
Дисперсия
- для несгруппированных данных: ![]()
- для вариационного ряда: 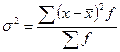
![]()
Коэффициент вариации (используется для характеристики однородности совокупности по исследуемому признаку)
![]() - до 17% – совокупность совершенно однородна, 17%-33% - достаточно однородна, >33% - неоднородна.
- до 17% – совокупность совершенно однородна, 17%-33% - достаточно однородна, >33% - неоднородна.
Сложение дисперсий
Величина общей дисперсии
(![]() ) характеризует вариацию признака под влиянием всех факторов, формирующих уровень признака у единиц данной совокупности
) характеризует вариацию признака под влиянием всех факторов, формирующих уровень признака у единиц данной совокупности
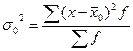 ,
, ![]() - общая средняя арифметическая для всей совокупности
- общая средняя арифметическая для всей совокупности
Межгрупповая дисперсия
(![]() ) отражает систематическую вариацию, т. е. различия в величине изучаемого признака, которые возникают под влиянием фактора, положенного в основу группировки
) отражает систематическую вариацию, т. е. различия в величине изучаемого признака, которые возникают под влиянием фактора, положенного в основу группировки
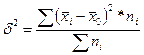 ,
,![]() - средняя в каждой группе,
- средняя в каждой группе, ![]() - число единиц в каждой группе
- число единиц в каждой группе
Средняя внутригрупповая дисперсия
(![]() ) характеризует случайную вариацию, возникающую под влиянием других, неучтенных факторов, и не зависит от условия (признака-фактора), положенного в основу группировки.
) характеризует случайную вариацию, возникающую под влиянием других, неучтенных факторов, и не зависит от условия (признака-фактора), положенного в основу группировки.
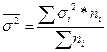 , где
, где 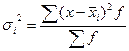 - дисперсия по отдельной группе
- дисперсия по отдельной группе
или 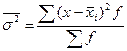
Равенство: ![]()
Корреляционное отношение
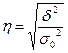 ,
, ![]() >0,5 – связь между групповым фактором и результирующим признаком – тесная,
>0,5 – связь между групповым фактором и результирующим признаком – тесная, ![]() <0,5 – связь слабая
<0,5 – связь слабая
Показатель асимметрии
![]() ,
, 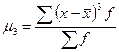 - центральный момент третьего порядка
- центральный момент третьего порядка
Средняя квадратическая ошибка: ![]() , n
– число наблюдений
, n
– число наблюдений
Если ![]() , асимметрия существенна и распределение признака в генеральной совокупности не является симметричным. Если
, асимметрия существенна и распределение признака в генеральной совокупности не является симметричным. Если ![]() , асимметрия несущественна, ее наличие объясняется влиянием случайных обстоятельств.
, асимметрия несущественна, ее наличие объясняется влиянием случайных обстоятельств.
![]() - правосторонняя асимметрия,
- правосторонняя асимметрия, ![]() - левосторонняя асимметрия.
- левосторонняя асимметрия.
Показатель эксцесса (островершинности)
![]() ,
, 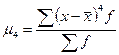 - центральный момент четвертого порядка
- центральный момент четвертого порядка
![]() >0 – высоковершинное,
>0 – высоковершинное, ![]() < 0 – низковершинное (
< 0 – низковершинное (![]() = -2 – предел)
= -2 – предел)
Средняя квадратическая ошибка: ![]() n
– число наблюдений
n
– число наблюдений
Кривые распределения
Кривая линия, которая отражает закономерность изменения частот в чистом, исключающем влияние случайных факторов виде, называется кривой распределения.
Плотность распределения (расчет теоретических частот)
![]() ,
, ![]() - нормированное отклонение
- нормированное отклонение
![]() ,
,![]() - определяется по таблице (приложение 1)
- определяется по таблице (приложение 1)
Критерий согласия К. Пирсона ( для проверки близости теоретического и эмпирического распределений, для проверки соответствия эмпирического распределения закону нормального распределения)
![]() f
– эмпирические частоты в интервале,
f
’
– теоретические частоты в интервале
f
– эмпирические частоты в интервале,
f
’
– теоретические частоты в интервале
Критерий согласия Романовского
![]() ,
m
– число групп,
m
-3 – число степеней свободы при исчислении частот нормального распределения
,
m
– число групп,
m
-3 – число степеней свободы при исчислении частот нормального распределения
Если к<3, то можно принять гипотезу о нормальном характере эмпирического распределения
Критерий Колмогорова
![]() , D
– максимальное значение разности между накопленными эмпирическими и теоретическими частотами,
n
– сумма эмпирических частот
, D
– максимальное значение разности между накопленными эмпирическими и теоретическими частотами,
n
– сумма эмпирических частот
Распределение Пуассона (теоретические частоты)
![]() ,
n
– общее число независимых испытаний, λ – среднее число появления редкого события в
n
одинаковых независимых испытаниях,
m
– частота данного события, е=2,71828
,
n
– общее число независимых испытаний, λ – среднее число появления редкого события в
n
одинаковых независимых испытаниях,
m
– частота данного события, е=2,71828
Выборочное наблюдение
N – объем генеральной совокупности
n – объем выборочной совокупности (число единиц, попавших в выборку)
![]() - генеральная средняя (среднее значение признака в генеральной совокупности)
- генеральная средняя (среднее значение признака в генеральной совокупности)
![]() - выборочная средняя
- выборочная средняя
р – генеральная доля (доля единиц, обладающих данным признаком в генеральной совокупности)
w – выборочная доля
![]() - генеральная дисперсия
- генеральная дисперсия
![]() - выборочная дисперсия
- выборочная дисперсия
![]() - среднее квадратическое отклонение признака в генеральной совокупности
- среднее квадратическое отклонение признака в генеральной совокупности
S – среднее квадратическое отклонение признака в выборочной совокупности.
Неравенство Чебышеба
При неограниченном числе наблюдений, независящих друг от друга из генеральной совокупности с вероятностью сколь угодно близкой к 1, можно утверждать, что расхождение между выборочной и генеральной средней будет сколь угодно малой величиной ![]() .
.
![]()
Теорема Ляпунова
Дает количественную оценку ошибки. При неограниченном объеме из генеральной совокупности с Р расхождения выборочной и генеральной средней равна интегралу Лапласа
![]() ,
, 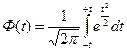 - нормированная функция Лапласа (интеграл Лапласа)
- нормированная функция Лапласа (интеграл Лапласа)
Р – гарантированная вероятность
t – коэффициент доверия, зависящий от Р
| Р |
0,683 |
0,954 |
0,997 |
| t |
1 |
2 |
3 |
![]() - предельная ошибка выборки
- предельная ошибка выборки
![]() ,
, ![]() - стандартная среднеквадратическая ошибка
- стандартная среднеквадратическая ошибка
![]() ,
, ![]() - предельная (максимально возможная) ошибка средней,
t
– коэффициент кратности средней ошибки выборки, зависящий от вероятности, с которой гарантируется величина предельной ошибки
- предельная (максимально возможная) ошибка средней,
t
– коэффициент кратности средней ошибки выборки, зависящий от вероятности, с которой гарантируется величина предельной ошибки
![]() ,
, ![]() - предельная (максимально возможная) ошибка доли
- предельная (максимально возможная) ошибка доли
Средняя ошибка (n>30) при случайной повторной выборке:
![]() ,
, ![]()
При случайной бесповторной выборке:
![]() ,
, ![]()
Формулы ошибок простой случайной выборки
| Способ отбора единиц |
||
| повторный |
бесповторный |
|
| Средняя ошибка μ: Для средней |
|
|
| Для доли |
|
|
| Предельная ошибка Δ: Для средней |
|
|
| Для доли |
|
|
Доверительные интервалы для генеральной средней –
![]()
Доверительные интервалы для генеральной доли –
![]()
Доверительная вероятность – функция от t, вероятность находится по приложению3
![]()
Формулы для определения численности простой и случайной выборки
| Способ отбора единиц |
||
| повторный |
бесповторный |
|
| Численность выборки (n): Для средней |
|
|
| Для доли* |
|
|
| * В случае, когда частость w даже приблизительно неизвестна, в расчет вводят максимальную величину дисперсии доли, равную 0,25 (если w=0,5, то w(1-w)=0,25). |
||
Типичная выборка
Применяется в тех случаях, когда из генеральной совокупности можно выделить однокачественные группы единиц (или однородные), затем из каждой группы случайно отобрать определенное число единиц в выборку.
Стандартная среднеквадратическая ошибка:
Повторный отбор - 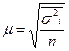 ,
, ![]() - средняя из внутригрупповых
- средняя из внутригрупповых
Бесповторный отбор - 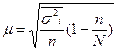
Отбор единиц при типичной выборке из каждой типичной группы:
1.Равное число единиц ![]() ,
, ![]() - число единиц, отобранных из
i
-ой типичной группы,
n
– общий объем,
R
– число групп
- число единиц, отобранных из
i
-ой типичной группы,
n
– общий объем,
R
– число групп
2.Пропорциональный отбор ![]() ,
, ![]() - доля
i
-ой группы в общем объеме генеральной совокупности
- доля
i
-ой группы в общем объеме генеральной совокупности
3.Отбор единиц с учетом вариации случайного признака ![]()
Серийная выборка
Вместо случайного отбора единиц совокупности осуществляется отбор групп (серий, гнезд). Внутри отобранных серий производится сплошное наблюдение.
Средняя стандартная ошибка:
Повторный отбор - ![]() ,
, ![]() , m
– число отобранных серий,
, m
– число отобранных серий, ![]() - средний уровень признака в серии,
- средний уровень признака в серии, ![]() - средний уровень признака для всей выборочной совокупности
- средний уровень признака для всей выборочной совокупности
Бесповторный отбор - ![]() , M
– общее число серий
, M
– общее число серий
Малые выборки
Выборки, при которых наблюдением охватывается небольшое число единиц (n<30)
Средняя ошибка малой выборки
![]() ,
, ![]()
Вероятность того, что генеральная средняя находится в определенных границах, определяется по формуле ![]() ,
, ![]() - значение функции Стьюдента (приложение 4)
- значение функции Стьюдента (приложение 4)
Корреляционная связь
Для оценки однородности совокупности – коэффициент вариации по факторным признакам
![]() , совокупность однородна, если
, совокупность однородна, если ![]() ≤ 33%
≤ 33%
Линейный коэффициент корреляции
Несгруппированные данные 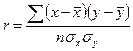
Сгруппированные данные - 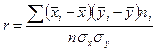
Оценка существенности линейного коэффициента корреляции
при большом объеме выборки ![]() ,
, ![]() . Если это отношение больше значения t-критерия Стьюдента (приложение 6, k=n-2, вероятность – 1-α)
. Если это отношение больше значения t-критерия Стьюдента (приложение 6, k=n-2, вероятность – 1-α)
при недостаточно большом объеме выборки ![]() ,
, ![]()
Корреляционное отношение
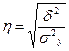 ,
, 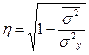 , где
, где 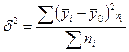 ,
, ![]() ,
, 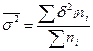
| Признаки |
А(да) |
|
Итого |
| В (да) |
a |
b |
a+b |
|
|
c |
d |
c+d |
| Итого |
a+c |
b+d |
n |
| A,b,c,d – частоты взаимного сочетания (комбинации) двух альтернативных признаков, n – общая сумма частот |
|||
Коэффициент ассоциации
![]()
Коэффициент контингенции
![]()
Уравнение регрессии
Линейная ![]()
Гиперболичская ![]()
Параболическая ![]()
Показательная ![]()
![]()
![]()
Для проверки возможности использования линейной функции определяется разность ![]() , если она <0,1 то можно применить линейную функцию.
, если она <0,1 то можно применить линейную функцию.
![]() ,m
– число групп
. Если
,m
– число групп
. Если ![]() < F-критерия, то можно. (Значение F-критерия определяется по таблице (приложение 5) α=0,05, число степеней свободы числителя (k1
= m-2) и знаменателя (k2
=n-m))
< F-критерия, то можно. (Значение F-критерия определяется по таблице (приложение 5) α=0,05, число степеней свободы числителя (k1
= m-2) и знаменателя (k2
=n-m))
Достоверность уравнения корреляционной зависимости ![]() ,
, 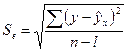 - средняя квадратическая ошибка,
y
– фактические значения результативного признака,
- средняя квадратическая ошибка,
y
– фактические значения результативного признака, ![]() - значения результативного признака, рассчитанные по уравнению регрессии,
l
– число параметров в уравнении регрессии.
- значения результативного признака, рассчитанные по уравнению регрессии,
l
– число параметров в уравнении регрессии.
Если это отношение не превышает 10-15%, то уравнение хорошо отображает изучаемую взаимосвязь.
Ряды динамики
Показатели динамики
| Показатель |
Метод расчета |
|
| С переменной базой (цепные) |
С постоянной базой (базисные) |
|
| Абсолютный прирост (показывает, на сколько в абсолютном выражении уровень текущего периода больше (меньше) базисного) |
|
|
| Коэффициент роста (показывает, во сколько раз уровень текущего периода больше (меньше) базисного) |
|
|
| Темп роста, % (это коэффициент роста, выраженный в %, показывает, сколько процентов уровень текущего периода составляет по отношению к уровню базисного периоа) |
|
|
| Темп прироста, % (показывает, на сколько % уровень текущего периода больше (меньше) уровня базисного периода) |
|
|
| Абсолютное значение 1% прироста (показывает, какая абсолютная величина скрывается за относительным показателем – одним процентом прироста) |
|
|
Средние показатели динамики
| Показатель |
Метод расчета |
| Средний уровень ряда -Для интервального ряда |
|
| -Для моментального ряда с равными интервалами |
|
| -Для моментального ряда с неравными интервалами |
|
| Средний абсолютный прирост |
|
| Средний коэффициент рост |
|
| Средний темп роста, % |
|
| Средний темп прироста, % |
|
| Средняя величина абсолютного значения 1% прироста |
|
Тренды
Линейный ![]()
![]()
![]()
Пусть ![]() =0, тогда если количество уровней в ряду динамики нечетное, то временные даты (t) будут (-2, -1, 0, 1, 2). Если четное, то (-5, -3, -1, 1, 3, 5)
=0, тогда если количество уровней в ряду динамики нечетное, то временные даты (t) будут (-2, -1, 0, 1, 2). Если четное, то (-5, -3, -1, 1, 3, 5)
Семестр 2 (Индексы)
Индекс – относительная величина, характеризующая изменение уровней сложных социально-экономических показателей во времени, в пространстве или по сравнению с планом.
Индивидуальный индекс физического объема выпуска продукции
![]()
Индивидуальный индекс цен
![]()
Индивидуальный индекс затрат на выпуск продукции
![]()
Индивидуальный индекс стоимости продукции
![]()
Агрегатный индекс физического объема продукции
(Относительное изменение физического объема продукции в отчетном периоде по сравнению с базисным) 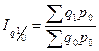
![]() - характеризует абсолютное изменение физического объема в относительном выражении без влияния ценового фактора.
- характеризует абсолютное изменение физического объема в относительном выражении без влияния ценового фактора.
Средний взвешенный арифметический индекс физического объема продукции
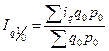 , iq
– индивидуальный индекс по каждому виду продукции
, iq
– индивидуальный индекс по каждому виду продукции
Средний взвешенный гармонический индекс физического объема продукции
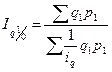
Агрегатный индекс цен
(характеризует среднее изменение цен по совокупности различных видов продукции) 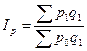
![]() - абсолютное изменение всей стоимости продукции за счет изменения цен
- абсолютное изменение всей стоимости продукции за счет изменения цен
Агрегатный индекс цен
(характеризует среднее изменение цен на потребительские товары) 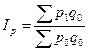
Агрегатный индекс затрат на выпуск всей продукции
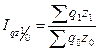
Двухфакторный индекс
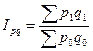
Связь: 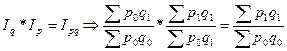
Индекс планового задания
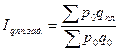
Индекс степени выполнения плана
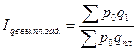
Связь: 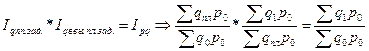
Изменение себестоимости продукта А по фирме ![]() , средняя себестоимость -
, средняя себестоимость - 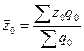
Индекс влияния структурных сдвигов в объеме продукции
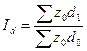 , d
0
– удельный вес каждого предприятия в общем объеме выпуска продукта А
, d
0
– удельный вес каждого предприятия в общем объеме выпуска продукта А
Абсолютное изменение общей стоимости продукции за счет двух факторов: ![]() , за счет изменения физического объема продукции -
, за счет изменения физического объема продукции -![]() , за счет изменения цен на продукцию -
, за счет изменения цен на продукцию -![]()
Абсолютное изменение общих затрат на выпуск продукции за счет двух факторов: ![]() , за счет изменения физического объема продукции -
, за счет изменения физического объема продукции - ![]() , за счет среднего изменения себестоимости единицы продукции -
, за счет среднего изменения себестоимости единицы продукции - ![]() .
.
Выработка - W = Q/T , W – выработка, Q – физический объем реализованной продукции/услуг, T – затраты живого труда (среднесписочная численность работников/рабочих)
Трудоемкость (показатель, обратный выработке) - t = 1/W = T/Q Трудоемкость характеризует величину затрат рабочего времени на единицу произведенной продукции.
Индекс динамики выработки переменного состава , определяющий отношение выработки отчетного периода к выработке базисного периода - Iw = W1 /W0
Этот индекс характеризует изменение производительности труда под влиянием всех факторов, а именно: НТП, человеческого фактора (квалификация и т.п.) и др.
Индекс динамики трудоемкости - It = t1 /t0
Индекс динамики трудоёмкости характеризует изменение трудоёмкости в отчетном периоде по сравнению с базисным, и его величина зависит от изменения трудоёмкости производимой продукции и от изменения объемов производства этой продукции.
IQ = IW * IT – система связанных индексов, которая позволяет определить влияние интенсивных и экстенсивных факторов на изменение объема продукции, услуг.
Среднегодовая стоимость основных фондов
в базисном и отчетном годах - ![]() ,
, ![]() - введенные в эксплуатацию фонды в течение года,
- введенные в эксплуатацию фонды в течение года, ![]() - число месяцев эксплуатации фондов в данном году,
- число месяцев эксплуатации фондов в данном году, ![]() - фонды, выбывшие из эксплуатации в течение года,
- фонды, выбывшие из эксплуатации в течение года, ![]() - число месяцев, оставшихся до конца года после выбытия фондов из эксплуатации.
- число месяцев, оставшихся до конца года после выбытия фондов из эксплуатации.
Фондоотдача
-![]() .
.
Фондоёмкость
– показатель, обратный фондоотдаче, за базисный и отчетный годы по формуле ![]()
Индекс динамики фондоотдачи
IV
п.с.
= ![]()
![]() =
= ![]() Этот индекс характеризует изменение фондоотдачи под влиянием всех факторов, включая НТП (новая техника, технология), человеческий фактор, структурный фактор, который на уровне АО может выражаться в изменении состава основных фондов в отчетном по сравнению с базисным годом.
Этот индекс характеризует изменение фондоотдачи под влиянием всех факторов, включая НТП (новая техника, технология), человеческий фактор, структурный фактор, который на уровне АО может выражаться в изменении состава основных фондов в отчетном по сравнению с базисным годом.
Индекс динамики фондоемкости
![]()
Влияние интенсивного (качественного) и экстенсивного (количественного) факторов на абсолютное изменение физического объема продукции/услуг. Под экстенсивным фактором обычно понимают абсолютное изменение основных фондов. Под интенсивным – абсолютное изменение показателя фондоотдачи.
Влияние экстенсивного фактора:
![]()
Влияние интенсивного фактора:
![]()
Влияние обоих факторов
:![]()
Показатели фондовооруженности рабочих
![]() ,
, ![]() - среднесписочная численность рабочих
.
- среднесписочная численность рабочих
.
Индекс динамики фондовооруженности:
![]()
Коэффициент износа основных фондов
на конец отчетного года ![]()
Износ фондов
на конец отчетного года ![]()
Похожие работы
-
Метод определения спроса на основе анализа цен и объемов продаж
Этот статистический метод позволяет прогнозировать основной тренд изменения спроса и его эластичность по цене. Он имеет значение для планирования базовых уровней цен для будущего периода, а также уточнения ценовых расчетов.
-
Управление качеством
Качество продукции и услуг – важнейший фактор эффективной деятельности предприятий в условиях рыночных методов хозяйствования. Техническое регулирование и качество. Роль и место стандартизации в управлении качеством.
-
Оценка конкурентоспособности ювелирных торговых предприятий г. Курска
Конкурентоспособность предприятия является сравнительным показателем. Она может быть оценена лишь путем сравнений условий, ресурсов и результатов деятельности конкретного торгового предприятия с определенной группой предприятий, которые определены его конкурентами.
-
Ясные критерии оценки бизнеса и деятельности организации
Решениям и действиям предшествует анализ. Для принятия рациональных финансовых решений менеджеру необходим аналитический инструментарий, на основе которого разрабатываются и обосновываются управленческие решения.
-
Планирование на предприятии
Натуральные, стоимостные, количественные, качественные, абсолютные и относительные показатели планов. Расчет фонда накопления предприятия.
-
Классификация методов разработки и принятия управленческих решений
В процессе разработки и принятия управленческих решений лицо, принимающее решение, может использовать различные методы, которые прямо или косвенно способствуют принятию оптимальных решений.
-
Регрессионная модель занятости населения. Показатели изменения фондовооруженности труда
Анализ интенсивности изменений в уровнях ряда динамики. Группировка продуктов питания. Разработка регрессионной модели занятости населения. Характеристика показателей интенсивности изменения фондовооруженности труда. Минимальная потребительская корзина.
-
по статистике товарооборот и издержки, анализ договоров по поставке ассортиме
Новосибирский Государственный Технический Университет Кафедра Финансов и Налоговой Политики Контрольная работа по статистике Выполнил: Студентка 3 курса ИДО, НГТУ, Боянова Евгения Игоревна
-
Билеты по менеджменту за 1 семестр 2-го курса 2003г.
Вопросы к экзамену по дисциплине «Менеджмент». Понятие менеджмента, организация, сущность деятельности менеджера. Понятие системы управления, субъект, объект управления, коммуникационные связи.
-
Формы документов и порядок их заполнения для проведения процедуры "Мозговой штурм"
Идея метода мозгового штурма Алекса Осборна - оперативный метод решения проблемы на основе стимулирования творческой активности участников. Этапы проведения мозгового штурма: постановка проблемы; генерация идей; группировка, отбор и оценка идей.
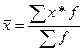 ,
,