Referat.me
/ / Елементи інформаційних технологій в математичному програмуванні

Название: Елементи інформаційних технологій в математичному програмуванні

Вид работы: реферат

Рубрика: Математика

Размер файла: 65.68 Kb

Скачать файл: referat.me-214667.docx

Краткое описание работы: Завдання 1 Розв'язати графічним способом при умовах: Розв'язування Зобразимо розв’язок системи нерівностей та вектор F (1;2): Максимум функції досягається в точці А:

Елементи інформаційних технологій в математичному програмуванні

Завдання 1

Розв'язати графічним способом при умовах:

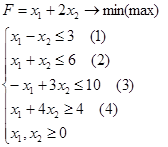
Розв'язування

Зобразимо розв’язок системи нерівностей та вектор F (1;2):

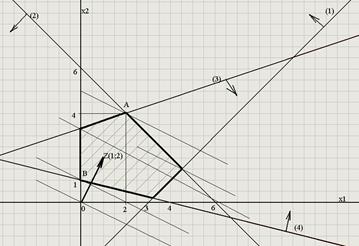
Максимум функції досягається в точці А:

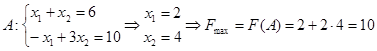
Мінімум функції досягається в точці В:


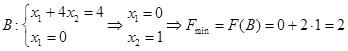
Завдання 2

Розв'язати транспортну задачу методом потенціалів.

Розв'язування

Спочатку перевіримо задачу на замкненість:

.

Задача є замкненою.

Вихідна таблиця:

А/В 10 20 25 40
25 4 7 2 5
15 9 3 4 6
35 8 5 9 3
20 2 1 7 4

Складемо початковий план методом мінімального елементу:

А/В 10 20 25 40
25 4 7 2 5
25
15 9 3 4 6
10 5
35 8 5 9 3
35
20 2 1 7 4
20

Опорний план є виродженим, адже число зайнятих клітинок менше ніж m+n-1=8. Зробимо його невиродженим, розміщуючи базисні нулі в клітину з координатами (i,j)=(1,1) та (4,1). Вирішимо задачу методом потенціалів:

А/В 10 20 25 40 U
25 4 7 2 5 0
0 25
15 9 - 3 + 4 6 5
10 5
35 8 5 9 3 2
35
20 2 + 1 - 7 4 -2
0 20
4 3 2 1 295

Сформуємо оціночну матрицю з елементів :

Оціночна матриця
0 4 0 4
0 -5 -3 0
2 0 5 0
0 0 7 5

План не є оптимальним, адже є від’ємні елементи.

Переміщуємо по циклу вантаж величиною 10 одиниць, додаючи цю величину у клітинах зі знаком «+», та віднімаючи її від клітин зі знаком «- ».


Маємо,

А/В 10 20 25 40 U
25 4 - 7 2 5 + 0
0 25
15 9 3 + 4 6 - 0
10 5
35 8 5 9 3 -3
35
20 2 + 1 - 7 4 -2
10 10
V 4 3 2 6 245
Оціночна матриця
0 4 0 -1
5 0 2 0
7 5 10 0
0 0 7 0

План не є оптимальним, адже є від’ємні елементи.

Переміщуємо по циклу вантаж величиною 0 одиниць, додаючи цю величину у клітинах зі знаком «+», та віднімаючи її від клітин зі знаком «- ».

Отримаємо,

А/В 10 20 25 40 U
25 4 7 2 5 0
25 0
15 9 3 4 6 1
10 5
35 8 5 9 3 -2
35
20 2 1 7 4 -1
10 10
V 3 2 2 5 245

Оціночна матриця
1 5 0 0
5 0 1 0
7 5 9 0
0 0 6 0

Як бачимо усі . Адже отриманий план є оптимальним.

При цьому загальна вартість перевезень складає 245 і є мінімальною.

Завдання 3

Розв'язати задачу ЛП симплекс-методом:

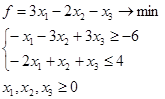
Розв'язування

Запишемо в канонічному виді:

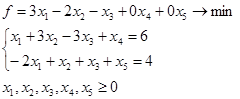
Вирішимо задачу симплекс методом.

Базис БП x 1 x 2 x 3 x 4 x 5
x4 6 1 3 -3 1 0
x5 4 -2 1 1 0 1
ИС 0 3 -2 -1 0 0
Обрано ключовий елемент (1,2)
Базис БП x 1 x 2 x 3 x 4 x 5
x2 2 1/3 1 -1 1/3 0
x5 2 -7/3 0 2 -1/3 1
ИС 4 11/3 0 -3 2/3 0
Обрано ключовий елемент (2,3)
Базис БП x 1 x 2 x 3 x 4 x 5
x2 3 -5/6 1 0 1/6 1/2
x3 1 -7/6 0 1 -1/6 1/2
ИС 7 1/6 0 0 1/6 3/2

Отримано оптимальний план x* = (0, 3, 1). За нього fmin = (x*) = -7.


Список використаних джерел

1. Бурий В.В., Шевченко І.В. Математичне програмування. — К.: НАУ, 2007. — 168с.

2. Єгоршин О.О., Малярець Л.М. Математичне програмування. — Х.: ВД "ІНЖЕК", 2006. — 383с.

3. Жильцов О.Б., Кулян В.Р., Юнькова О.О. Математичне програмування (з елементами інформаційних технологій) / Міжрегіональна академія управління персоналом / Олена Олександрівна Юнькова (ред.). — К.: МАУП, 2006. — 184с.

4. Зеленський К.Х. Математичне програмування. — К.: Університет "Україна", 2007. — 241c.

5. Івченко І.Ю. Математичне програмування. — К.: Центр учбової літератури, 2007. — 232с.

6. Лебідь М.Т., Синявіна Ю.В. Математичне програмування. — Х., 2007. — 72с.

Похожие работы