Название: Диференціальні операції в скалярних і векторних полях. Основні поняття і формули
Вид работы: реферат
Рубрика: Математика
Размер файла: 497.94 Kb
Скачать файл: referat.me-214674.docx
Краткое описание работы: Диференціальні операції в скалярних і векторних полях. Основні поняття і формули 1. Скалярне поле Нехай – область у тривимірному просторі (або на площині). Кажуть, що в області
Диференціальні операції в скалярних і векторних полях. Основні поняття і формули
Диференціальні операції в скалярних і векторних полях. Основні поняття і формули
1. Скалярне поле
Нехай ![]() – область у тривимірному просторі (або на площині). Кажуть, що в області
– область у тривимірному просторі (або на площині). Кажуть, що в області ![]() задано скалярне поле, якщо кожній точці
задано скалярне поле, якщо кожній точці ![]() поставлено у відповідність деяке число
поставлено у відповідність деяке число ![]() .
.
Прикладами скалярних полів є поле температури даного тіла, поле густини даного неоднорідного середовища, поле вологості повітря, поле атмосферного тиску, поле потенціалів заданого електростатичного поля тощо.
Поверхня (лінія), на якій функція ![]() набуває одне й те саме значення, називається поверхнею (лінією) рівня скалярного поля (наприклад, поверхні або лінії постійної температури). Надаючи
набуває одне й те саме значення, називається поверхнею (лінією) рівня скалярного поля (наприклад, поверхні або лінії постійної температури). Надаючи ![]() різних постійних значень:
різних постійних значень: ![]() , отримаємо сім’ю поверхонь (ліній) рівня даного скалярного поля.
, отримаємо сім’ю поверхонь (ліній) рівня даного скалярного поля.
Фізичні скалярні поля не залежать від вибору системи координат: величина ![]() є функцією лише точки
є функцією лише точки ![]() і, можливо, часу (нестаціонарні поля).
і, можливо, часу (нестаціонарні поля).
Якщо в просторі ввести прямокутну систему координат ![]() , то точка
, то точка ![]() у цій системі координат матиме певні координати
у цій системі координат матиме певні координати ![]() і скалярне поле
і скалярне поле ![]() стане функцією цих координат:
стане функцією цих координат: ![]() .
.
2. Векторне поле
Кажуть, що в області ![]() задано векторне поле, якщо кожній точці
задано векторне поле, якщо кожній точці ![]() поставлено у відповідність деякий вектор
поставлено у відповідність деякий вектор ![]() .
.
Фізичні приклади векторних полів: електричне поле системи електричних зарядів, яке характеризується в кожній точці вектором напруженості ![]() ; магнітне поле, утворене електричним струмом і яке характеризується в кожній точці вектором магнітної індукції
; магнітне поле, утворене електричним струмом і яке характеризується в кожній точці вектором магнітної індукції ![]() ; поле тяжіння, утворене системою мас і яке характеризується в кожній точці вектором сили тяжіння
; поле тяжіння, утворене системою мас і яке характеризується в кожній точці вектором сили тяжіння ![]() , що діє в цій точці на одиничну масу; поле швидкостей потоку рідини, яке описується в кожній точці вектором швидкості
, що діє в цій точці на одиничну масу; поле швидкостей потоку рідини, яке описується в кожній точці вектором швидкості ![]() .
.
Зручною геометричною характеристикою векторногополя ![]() є векторні лінії – криві, в кожній точці
є векторні лінії – криві, в кожній точці ![]() яких вектор
яких вектор ![]() напрямлений по дотичній до кривої. Векторні лінії поля тяжіння, електричного і магнітного полів називається силовими лініями, а поля швидкостей – лініями струму.
напрямлений по дотичній до кривої. Векторні лінії поля тяжіння, електричного і магнітного полів називається силовими лініями, а поля швидкостей – лініями струму.
Нехай векторна лінія, яка проходить через точку ![]() , описується рівнянням
, описується рівнянням ![]() , де
, де ![]() – параметр. Умова колінеарності вектора поля
– параметр. Умова колінеарності вектора поля ![]() і дотичного вектора
і дотичного вектора ![]() в довільній точці цієї лінії має вигляд
в довільній точці цієї лінії має вигляд
![]() ,(1)
,(1)
де ![]() – деяке число. Умову (1) можна записати також у вигляді
– деяке число. Умову (1) можна записати також у вигляді
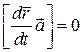 (2)
(2)
або, помноживши на ![]() , у вигляді
, у вигляді
![]() .(3)
.(3)
Кожне із рівнянь (1) – (3) є диференціальним рівнянням векторних ліній у векторній формі і визначає множину векторних ліній. Конкретна векторна лінія, яка проходить через задану точку ![]() , визначається додатковою умовою
, визначається додатковою умовою
![]() ,(4)
,(4)
де ![]() – радіус-вектор точки
– радіус-вектор точки ![]() .
.
Фізичні векторні поля не залежать від системи координат: в кожній точці ![]() вектор
вектор ![]() повністю визначається своїм модулем
повністю визначається своїм модулем ![]() і напрямом. Якщо в просторі введена прямокутна система координат
і напрямом. Якщо в просторі введена прямокутна система координат![]() , то векторне поле
, то векторне поле ![]() описується вектор-функцією трьох змінних
описується вектор-функцією трьох змінних ![]() або трьома скалярними функціями – її координатами:
або трьома скалярними функціями – її координатами:
![]() .
.
Оскільки в прямокутних координатах![]() , то векторне рівняння (3) для векторних ліній еквівалентне системі диференціальних рівнянь
, то векторне рівняння (3) для векторних ліній еквівалентне системі диференціальних рівнянь
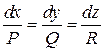 ,(5)
,(5)
а додаткове векторне рівняння (4) еквівалентне таким умовам:
![]() ,(6)
,(6)
де ![]() – координати точки
– координати точки![]() .
.
3. Похідна за напрямом
Скалярне і векторне поля
![]() і
і ![]()
Називаються диференційованими ![]() разів, якщо функції
разів, якщо функції
![]()
диференційовані ![]() разів. Надалі розглядатимемо поля, диференційовані потрібне нам число разів.
разів. Надалі розглядатимемо поля, диференційовані потрібне нам число разів.
Нехай ![]() – скалярне поле, задане в області
– скалярне поле, задане в області ![]() ,
, ![]() – одиничний фіксований вектор;
– одиничний фіксований вектор; ![]() – фіксована точка;
– фіксована точка; ![]() – довільна точка із
– довільна точка із ![]() , відмінна від
, відмінна від ![]() і така, що вектор
і така, що вектор ![]() колінеарний
колінеарний ![]() . Нехай, далі,
. Нехай, далі, ![]() – величина напрямленого відрізка
– величина напрямленого відрізка ![]() (вона дорівнює його довжині
(вона дорівнює його довжині 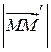 , якщо напрям вектора
, якщо напрям вектора ![]() збігається з напрямом вектора
збігається з напрямом вектора ![]() , і дорівнює –
, і дорівнює – ![]() , якщо вектори
, якщо вектори 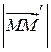 і
і ![]() є протилежними).
є протилежними).
Означення.
Число![]() називається похідною скалярного поля
називається похідною скалярного поля ![]() (функції
(функції![]() ) в точці
) в точці ![]() за напрямом
за напрямом ![]() і позначається символом
і позначається символом![]() .
.
Похідна за напрямом ![]() є швидкістю зміни функції
є швидкістю зміни функції ![]() за напрямом
за напрямом ![]() в точці
в точці![]() .
.
Якщо в прямокутній системі координат ![]()
![]() , то
, то
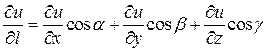 .(7)
.(7)
Зокрема, якщо вектор ![]() збігається з одним із ортів
збігається з одним із ортів ![]() або
або ![]() , то похідна за напрямком
, то похідна за напрямком ![]() збігається з відповідною частинною похідною. Наприклад, якщо
збігається з відповідною частинною похідною. Наприклад, якщо ![]() , то
, то
![]() .
.
Аналогічно визначається похідна за напрямом векторного поля.
Означення
. Вектор 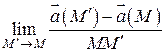 називається похідною векторного поля
називається похідною векторного поля ![]() (вектор-функції
(вектор-функції![]() ) в точці
) в точці ![]() за напрямом
за напрямом ![]() і позначається символом
і позначається символом![]() .
.
Якщо в прямокутній системі координат ![]()
![]() , то
, то
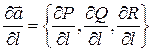 .
.
4. Градієнт скалярного поля
скалярне векторне поле дивергенція
Означення
. Градієнтом скалярного поля ![]() називається вектор-функція
називається вектор-функція
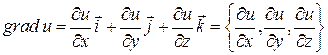 .
.
Із рівності (7) випливає, що
![]() ,(8)
,(8)
Звідси ![]() , оскільки
, оскільки ![]() .
.
Тут ![]() – кут між векторами
– кут між векторами ![]() і
і ![]() в точці
в точці![]() . Очевидно, що
. Очевидно, що ![]() має найбільше значення при
має найбільше значення при![]() , тобто у напрямі
, тобто у напрямі ![]() в даній точці. Інакше кажучи, вектор
в даній точці. Інакше кажучи, вектор ![]() в даній точці вказує напрям найбільшого зростання поля
в даній точці вказує напрям найбільшого зростання поля ![]() (функції
(функції ![]() ) у цій точці, а
) у цій точці, а ![]() є швидкість зростання функції
є швидкість зростання функції ![]() в цьому напрямі. Таким чином, вектор
в цьому напрямі. Таким чином, вектор ![]() не залежить від вибору системи координат, а його модуль і напрям у кожній точці визначається самою функцією
не залежить від вибору системи координат, а його модуль і напрям у кожній точці визначається самою функцією![]() .
.
5. Потенціальне поле
Означення.
Векторне поле ![]() називається потенціальним в області
називається потенціальним в області![]() , якщо воно збігається в області
, якщо воно збігається в області ![]() з полем градієнта деякого скалярного поля
з полем градієнта деякого скалярного поля![]() :
:
![]() .(9)
.(9)
Функція ![]() називається скалярним потенціалом векторного поля
називається скалярним потенціалом векторного поля![]() . Якщо
. Якщо![]() , то із рівності (9) випливає, що
, то із рівності (9) випливає, що
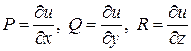 .
.
Інколи потенціалом векторного поля ![]() називають таку функцію
називають таку функцію ![]() , що
, що ![]() .
.
Розглянемо, наприклад, поле тяжіння точкової маси ![]() , розміщеної на початку координат. Воно описується вектор-функцією
, розміщеної на початку координат. Воно описується вектор-функцією ![]() (
(![]() – гравітаційна стала,
– гравітаційна стала, ![]() ). З такою силою діє це поле на одиничну масу, розміщену в точці
). З такою силою діє це поле на одиничну масу, розміщену в точці ![]() . Поле тяжіння є потенціальним. Його можна подати у вигляді градієнта скалярної функції
. Поле тяжіння є потенціальним. Його можна подати у вигляді градієнта скалярної функції ![]() , яка називається ньютонівським потенціалом поля тяжіння точкової маси
, яка називається ньютонівським потенціалом поля тяжіння точкової маси ![]() . Дійсно
. Дійсно
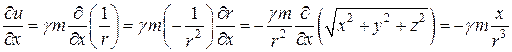 .
.
Аналогічно 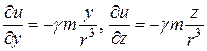 , звідси
, звідси
![]() .
.
Далі, розглянемо ще один приклад. Нехай задано електричне поле точкового заряду ![]() , розміщеного на початку координат. Воно описується в точці
, розміщеного на початку координат. Воно описується в точці ![]() вектором напруженості
вектором напруженості
![]() .
.
Це поле також є потенціальним полем. Його можна подати у вигляді ![]() . Функція
. Функція ![]() називається потенціалом електричного поля точкового заряду
називається потенціалом електричного поля точкового заряду ![]() .
.
Поверхні рівня потенціала ![]() називаються еквіпотенціальними поверхнями.
називаються еквіпотенціальними поверхнями.
6. Дивергенція
Означення
. Дивергенцією векторного поля ![]() називається скалярна функція
називається скалярна функція
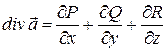 .
.
Слово «дивергенція» означає «розбіжність».
Дивергенція характеризує густину джерел даного векторного поля в розглянутій точці.
Розглянемо, наприклад, електричне поле точкового заряду ![]() , розміщеного в початку координат:
, розміщеного в початку координат:
![]() ,
,
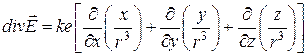 .
.
Оскільки 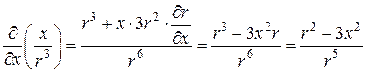 , і аналогічно
, і аналогічно 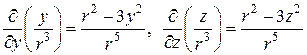 , то
, то 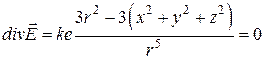
(при ![]() ). Цей результат означає відсутність поля у довільній точці, крім початку координат. В початку координат
). Цей результат означає відсутність поля у довільній точці, крім початку координат. В початку координат ![]() .
.
7. Ротор
Означення. Ротором (або вихором) векторного поля
![]()
називається вектор-функція
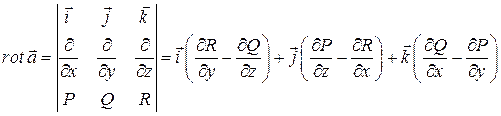 .
.
Зокрема, для плоского поля ![]() маємо
маємо
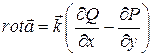 .
.
Розглянемо тверде тіло, яке обертається навколо осі ![]() із сталою кутовою швидкістю
із сталою кутовою швидкістю ![]() (рис. 1).
(рис. 1).
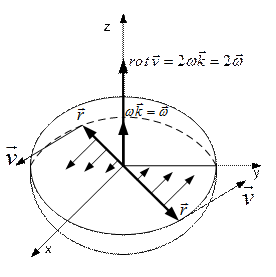
Рисунок 1 – Тверде тіло, яке обертається навколо осі ![]()
Векторне поле швидкостей ![]() точок цього тіла можна подати у вигляді
точок цього тіла можна подати у вигляді
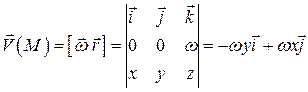 .
.
Знайдемо ротор поля швидкостей ![]() :
:
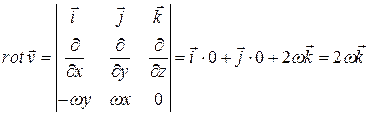 .
.
Таким чином, ![]() є сталим вектором, напрямленим уздовж осі обертання
є сталим вектором, напрямленим уздовж осі обертання ![]() , а його модуль дорівнює подвоєній кутовій швидкості обертання тіла:
, а його модуль дорівнює подвоєній кутовій швидкості обертання тіла:
![]() .
.
Розглянемо потенціальне поле ![]() . Його потенціал
. Його потенціал 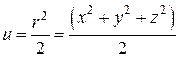 . Обчислимо ротор цього поля:
. Обчислимо ротор цього поля:
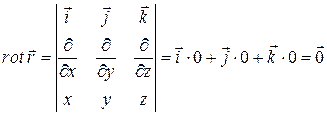 .
.
Взагалі, ротор довільного потенціального поля дорівнює нулю (див. підрозділ 2). Тому кажуть, що потенціальне поле є безвихровим.
8. Соленоїдальне поле
Векторне поле ![]() називається соленоїдальним в області
називається соленоїдальним в області ![]() , якщо в цій області
, якщо в цій області ![]() . Оскільки
. Оскільки ![]() характеризує густину джерел поля
характеризує густину джерел поля![]() , то в тій області, де поле соленоїдальне, немає джерел цього поля.
, то в тій області, де поле соленоїдальне, немає джерел цього поля.
Наприклад, електричне поле ![]() точкового заряду соленоїдальне (задовольняє умову
точкового заряду соленоїдальне (задовольняє умову ![]() ) всюди поза точкою, де знаходиться заряд (в цій точці
) всюди поза точкою, де знаходиться заряд (в цій точці ![]() ). Векторні лінії соленоїдального поля не можуть починатися або закінчуватися на межі області, або бути замкненими кривими. Прикладом соленоїдального поля з замкненими векторними лініями є магнітне поле, яке створюється струмом у провіднику.
). Векторні лінії соленоїдального поля не можуть починатися або закінчуватися на межі області, або бути замкненими кривими. Прикладом соленоїдального поля з замкненими векторними лініями є магнітне поле, яке створюється струмом у провіднику.
Якщо векторне поле ![]() можна подати як ротор деякого векторного поля
можна подати як ротор деякого векторного поля ![]() , тобто
, тобто ![]() , то вектор – функція
, то вектор – функція ![]() називається векторним потенціалом поля
називається векторним потенціалом поля ![]() .
.
Можна перевірити (див. докладніше п. 2), що ![]() , тобто поле
, тобто поле ![]() є соленоїдальним.
є соленоїдальним.
Довільне векторне поле можна подати у вигляді суми потенціального і соленоїдального полів.
9. Оператор Гамільтона
Згадаємо, що символ ![]() називається оператором частинної похідної по
називається оператором частинної похідної по ![]() . Під добутком цього оператора на функцію
. Під добутком цього оператора на функцію ![]() розумітимемо частинну похідну
розумітимемо частинну похідну ![]() , тобто
, тобто ![]() . Аналогічно,
. Аналогічно, ![]() і
і ![]() – оператори частинних похідних по
– оператори частинних похідних по ![]() і по
і по ![]() .
.
Введемо векторний оператор «набла» або оператор Гамільтона:
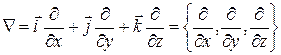 .
.
За допомогою цього символічного (операторного) «вектора» зручно записувати і виконувати операції векторного аналізу.
У результаті множення вектора ![]() на скалярну функцію
на скалярну функцію ![]() отримуємо
отримуємо ![]() :
:
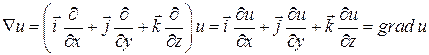 .
.
Скалярний добуток вектора ![]() на вектор – функцію
на вектор – функцію ![]() дає
дає![]() :
:
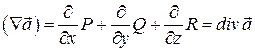 .
.
Векторний добуток вектора ![]() на вектор – функцію
на вектор – функцію ![]() дає
дає![]() :
:
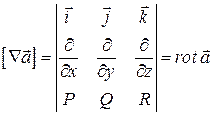 .
.
10. Нестаціонарні поля
Нехай в області ![]() визначено нестаціонарне скалярне поле
визначено нестаціонарне скалярне поле ![]() : величина
: величина ![]() є функцією точки
є функцією точки ![]() і часу
і часу ![]() . Приклад такого поля – змінний з часом розподіл температури в будь-якому середовищі (наприклад, в потоці рідини). Розглянемо точку
. Приклад такого поля – змінний з часом розподіл температури в будь-якому середовищі (наприклад, в потоці рідини). Розглянемо точку ![]() , яка рухається в області
, яка рухається в області ![]() (частинку рідини). Координати точки (частинки) змінюються з часом за відомим законом
(частинку рідини). Координати точки (частинки) змінюються з часом за відомим законом ![]() . Величина
. Величина ![]() в рухомій точці
в рухомій точці ![]() є складеною функцією
є складеною функцією ![]() :
:
![]() .
.
Обчислимо похідну по ![]() цієї функції (вона називається повною похідною). За правилом диференціювання складеної функції знаходимо
цієї функції (вона називається повною похідною). За правилом диференціювання складеної функції знаходимо
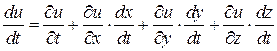 .
.
Вводячи в точці ![]() вектор швидкості
вектор швидкості 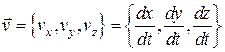 , отримуємо
, отримуємо
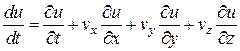
Або
![]() .(11)
.(11)
Аналогічно, якщо в області ![]() задано нестаціонарне векторне поле
задано нестаціонарне векторне поле ![]() , то для рухомої точки
, то для рухомої точки ![]() векторна величина
векторна величина ![]() є складеною функцією
є складеною функцією ![]() :
: ![]() . Повну похідну по
. Повну похідну по ![]() для кожної координати вектор – функції
для кожної координати вектор – функції ![]() можна обчислити за формулою (11). Помноживши результати на базисні вектори
можна обчислити за формулою (11). Помноживши результати на базисні вектори ![]() і складаючи, отримуємо
і складаючи, отримуємо
![]() .(12)
.(12)
У формулах (11) і (12) доданки ![]() і
і ![]() виражають швидкості зміни величин
виражають швидкості зміни величин ![]() та
та ![]() з часом при фіксованих координатах, тобто характеризують локальні зміни цих величин, і тому називаються локальними похідними. Доданки
з часом при фіксованих координатах, тобто характеризують локальні зміни цих величин, і тому називаються локальними похідними. Доданки ![]() і
і ![]() утворюються за рахунок зміни координат точки, її руху (конвекції). Тому ці доданки у виразах повних похідних називаються конвективними похідними.
утворюються за рахунок зміни координат точки, її руху (конвекції). Тому ці доданки у виразах повних похідних називаються конвективними похідними.
Локальні похідні характеризують нестаціонарність розглянутого поля у даній точці простору. Конвективні похідні характеризують неоднорідність поля у даний момент часу.
Похожие работы
-
Інтегральні характеристики векторних полів
інтегральні характеристики векторних полів 1. Диференціальні операції другого порядку Нехай в області задані скалярне поле і векторне поле , причому функції
-
Основні теореми теорії ймовірностей
Тема 2. Основні теореми теорії імовірності На фундаменті міцному будем класти поверхи, перегородки та сходинки, що їх з’єднають на віки. План. Теорема додавання імовірностей несумісних подій..
-
Алгебра висловлень
Реферат на тему: Алгебра висловлень Носієм алгебри висловлень є множина так званих простих висловлень. Просте елементарне висловлення (висловлювання) - це просте твердження, тобто розповідне речення, щодо змісту якого доречно ставити питання про його правильність або неправильність.
-
Загальні властивості неперервних функцій
Загальні властивості неперервних функцій однакові як для функцій однієї змінної, так і для функцій багатьох змінних. Теорема 3. (Вейєрштрасса). Функція
-
Функція, її границя та неперервність
Суть функції багатьох змінних, її означення і символіки. Границя і неперервність функції багатьох змінних. Визначення відкритої та замкненої області. Множина точок площини, для яких задана формула має зміст, як область визначення. Функція двох змінних.
-
Диференціальні рівняння першого порядку,
Реферат на тему: Диференціальні рівняння першого порядку, не розв’язані відносно похідної. 1. Основні поняття і означення, теорема про достатні умови існування і єдності розв’язку.
-
Диференціальні рівняння першого порядку, розвязані відносно похідної
Реферат на тему: Диференціальні рівняння першого порядку, розв язані відносно похідної 1. Поняття диференціального рівняння, його порядок. Означення 2.1.
-
Аналітична геометрія
Реферат на тему: Аналітична геометрія в просторі Аналітична геометрія в просторі Загальне рівняння площини в тривимірному просторі, яка проходить через точку (x0;y0;z0) перпендикулярно до вектора
-
Диференціальне рівняння
Основи означення. Диференціальні рівняння І порядку. Задача Коші. Теорема існування та єдності розв'язку. Економічні задачі, що потребують використання диференціального рівняння.
-
Застосування частинних похідних
Побудова дотичної площини та нормалі до поверхні. Геометричний зміст диференціала функції двох змінних. Поняття скалярного поля, зв'язок між градієнтом і похідною в даній точці. Формула Тейлора для функції двох змінних та її локальні екстремуми.