Название: Геометрические преобразования графиков функции
Вид работы: контрольная работа
Рубрика: Математика
Размер файла: 55.63 Kb
Скачать файл: referat.me-215135.docx
Краткое описание работы: Построение графиков функций F(x), симметричное их отбражение относительно оси координат ОХ, ОУ, при значениях -F, -x. Особенности построения графиков функций и симметричное отображение относительно осей координат: f(x)+A; f(x+а); kf(x); |f(x)|; |f(|x|)|.
Геометрические преобразования графиков функции
| № | Функция | Преобразование | Графики |
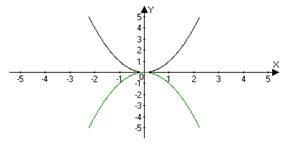
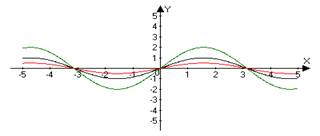
| 1 | y = −ƒ(x) | Сначала строим график функции ƒ(x), а затем симметрично отображаем его относительно оси OX. | y = − (x2 ) y = x2 → − (x2 )
|
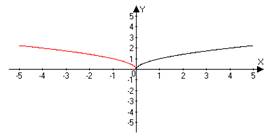
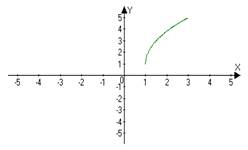
| 2 | y = ƒ(−x) | Сначала строим график функции ƒ(x), а затем симметрично отображаем его относительно оси OY. | y = √ (− x) y =√(x) → √ (− x)
|
| 3 | y = ƒ(x) +A A - const |
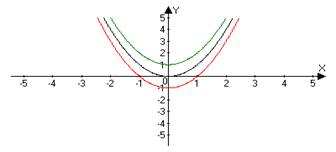
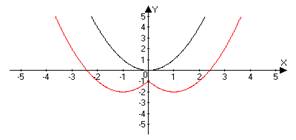
Сначала строим график функции ƒ(x), а затем, если А>0 поднимаем полученный график на А единиц вверх по оси OY. Если А<0, то опускаем вниз. | y = x2 → x2 +1 y = x2 → x2 –1
|
| 4 | y = ƒ(x−а) | Сначала строим график функции ƒ(x), а затем, если а>0, то график функции смещаем на а единиц вправо, а если а<0, то на а единиц влево. "−" − → "+" − ← |
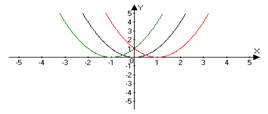
y = x2 → (x+1)2 y = x2 → (x -1)2
|
| 5 | y = K ƒ(x ) k − const k>0 |
Сначала строим график функции ƒ(x), а затем, если K>0, то растягиваем полученный график в K раз вдоль оси OY. А если 0< K<1, то сжимаем полученный график в 1 ∕ Kраз вдоль оси OY. ↕ ↓ ↑ |
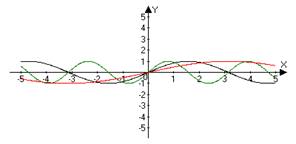
y = sin(x) → 2 sin(x) y = sin(x) → ½ sin(x)
|
6 7 |
y = ƒ(к x ) k − const k>0 y = A ƒ(к x+а) +В A, к, а, В − const |
Сначала строим график функции ƒ(x), а затем, если к >1, то сжимаем полученный график в к раз вдоль оси OХ. А если 0< к <1, то растягиваем полученный график в 1∕ к раз вдоль оси OХ. к >1 − →← 0< к <1 − ←→ ƒ( x ) → ƒ(к x ) → ƒ(к( х + а ∕ к )) →A ƒ(к( х + а ∕ к )) → A ƒ(к( х + а ∕ к )) +В |
y = sin(x) → sin(2 x) y = sin(x) → sin (½ x)
y = 2√(2x-2)+1 y =√x →√2x→√2(x -1) → 2√2(x -1) →2√2(x-1)+1
|
| 8 | y = │ƒ(x)│ | Сначала строим график функции ƒ(x), а затем часть графика, расположенную выше оси ОХ оставляем без изменения, а часть графика, расположенную ниже оси ОХ, заменяем симметричным отображением относительно ОХ. | y =│x3 │ y = x3 →│x3 │
|
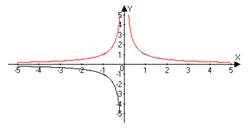
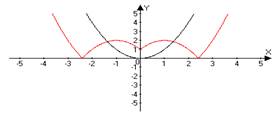
| 9 | y = ƒ(│x│) | Сначала строим график функции ƒ(x), а затем часть графика, расположенную правее оси ОУ, оставляем без изменения, а левую часть графика заменяем симметричным отображением правой относительно ОУ. | y = (│x│−1)2 −2 y = x2 →(x -1)2 → (x -1)2 − 2→(│x│−1)2 −2
|
| 10 | y = │ƒ(│x│)│ | ƒ(x) → ƒ(│x│) →│ƒ(│x│)│ | y= │(│x│−1)2 - 2│ y= x2 → (x-1)2 →(x-1)2 - 2→(│x│−1)2 - 2→│(│x│−1)2 - 2│
|
Похожие работы
-
Преобразование графиков функции
Тема: « Преобразование графиков функции Цели: 1) Систематизировать приемы построения графиков. 2) Показать их применение при построении: а) графиков сложных функций;
-
Геометрические преобразования графиков функции
Функция Преобразование Графики y = −ѓ(x) Сначала строим график функции ѓ(x), а затем симметрично отображаем его относительно оси OX. − (x2)
-
Графическое решение уравнений
График функции как множество всех точек координатной плоскости, абсциссы которых равны значениям аргументов, а ординаты – соответствующим значениям функции. Исследование графиков функций и графическое решение уравнений, их разновидности и особенности.
-
Антье и ее окружение
Антье и ее свойства. Графики антье.
-
Геометрические свойства кривых второго порядка
Цель курсовой работы Исследовать и изучить геометрические свойства кривых второго порядки (эллипса, гиперболы и параболы), представляющих собой линии пересечения кругового конуса с плоскостями, не проходящими через его вершины, а также научиться строить графики данных кривых в канонической и прямоугольной декартовой системах координат.
-
Декартовыми прямоугольными координатами
Декартовыми прямоугольными координатами точки P на плоскости в двухмерной системе координат называются взятые с определенным знаком расстояния (выраженные в единицах масштаба) этой точки до двух взаимно перпендикулярных прямых — осей координат или проекции радиус-вектора r точки P на две взаимно перпендикулярные координатные оси.
-
Функционально-графический подход к решению задач с параметрами
Выполнение алгебраических преобразований, логическая культура и техника исследования. Основные типы задач с параметрами, нахождение количества решений в зависимости от значения параметра. Основные методы решения задач, методы построения графиков функций.
-
Применение графиков в решении уравнений
Графическое решение квадратного уравнения. Системы уравнений. Тригонометрические уравнения. Тригонометрические неравенства.
-
График
Связи между алгеброй и геометрией были известны еще древним математикам. Например, длина отрезка выражается числом, а ведь отрезок — геометрическая фигура, тогда как числа изучаются в алгебре.
-
Кривые и поверхности второго порядка
Исследование кривой второго порядка. Определение типа кривой с помощью инвариантов. Приведение к каноническому виду, построение графиков. Исследование поверхности второго порядка. Определение типа поверхности. Анализ формы поверхности методом сечений.