Название: Преобразование графиков функции

Вид работы: реферат

Рубрика: Математика

Размер файла: 2.41 Mb

Скачать файл: referat.me-218336.pptx

Краткое описание работы: Тема: « Преобразование графиков функции Цели: 1) Систематизировать приемы построения графиков. 2) Показать их применение при построении: а) графиков сложных функций;

Преобразование графиков функции

Тема: « Преобразование графиков функции »

Цели:

1) Систематизировать приемы построения графиков.

2) Показать их применение при построении:

а) графиков сложных функций;

б) при решении заданий ЕГЭ из части C.

Рассмотрим основные правила преобразования графиков на примерах элементарных функций

1) Преобразование симметрии относительно оси x
f(x)  -f(x)

График функции y=-f(x) получается преобразованием симметрии графика функции y=f(x) относительно оси x.

Замечание. Точки пересечения графика с осью x остаются неиз мен ными.

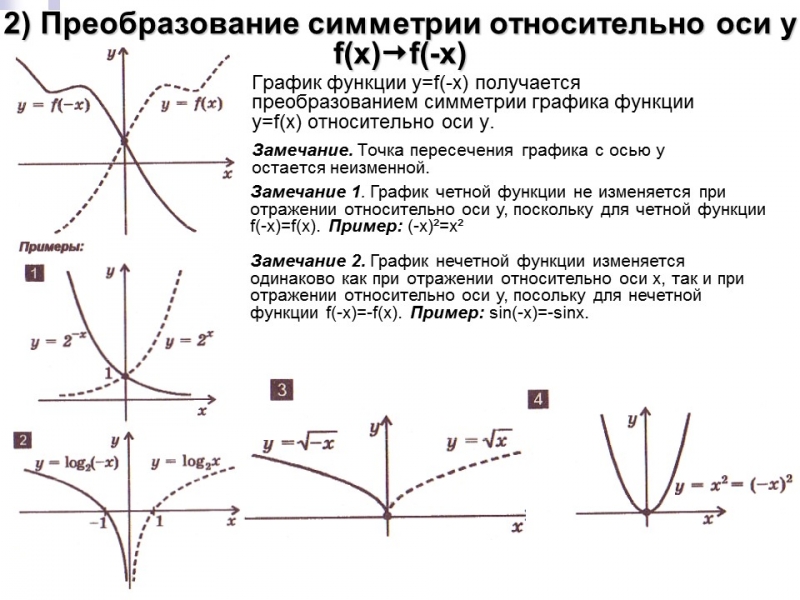
2) Преобразование симметрии относительно оси y
f(x)  f( - x)

График функции y=f(-x) получается преобразованием симметрии графика функции y=f(x) относительно оси y.

Замечание. Точка пересечения графика с осью y остается неизменной.

3) Параллельный перенос вдоль оси x
f(x) f(x-a)

График функции y=f(x-a) получается параллельным переносом графика функции y=f(x) вдоль оси x на |a| вправо при a>0 и влево при a<0.

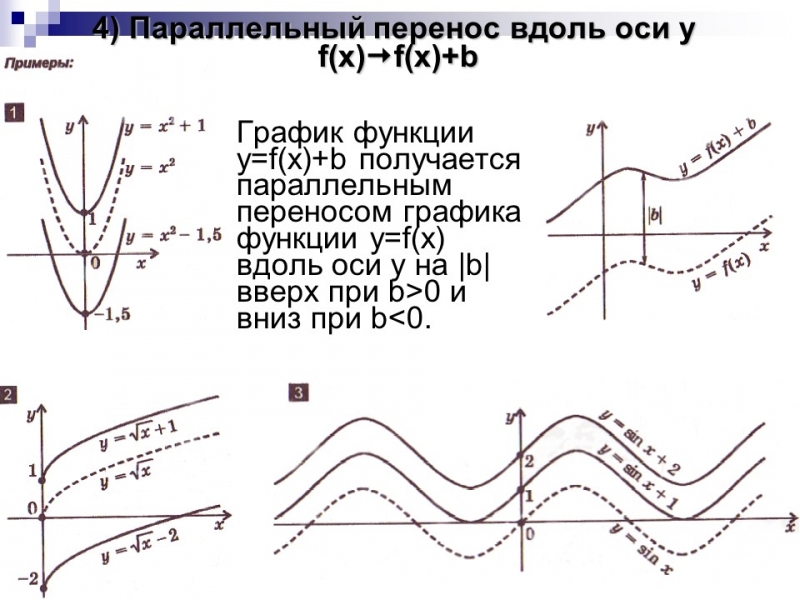
4) Параллельный перенос вдоль оси y
f(x)  f(x)+b

График функции y=f(x)+b получается параллельным переносом графика функции y=f(x) вдоль оси y на |b| вверх при b>0 и вниз при b<0.

5) Сжатие и растяжение вдоль оси x
f(x)  f(  x), где  >0

>1 График функции y=а(x) получается сжатием графика функции y=f(x) вдоль оси x в  раз.

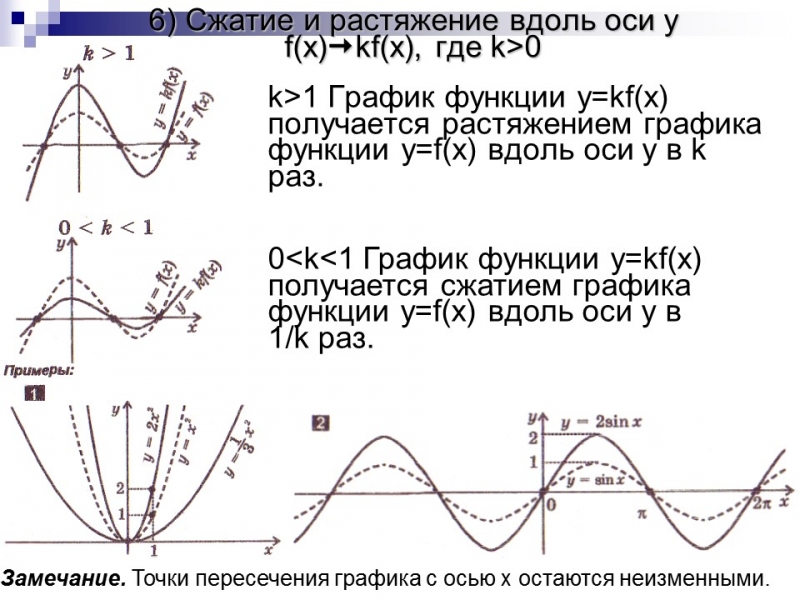
6) Сжатие и растяжение вдоль оси y
f(x) kf(x), где k>0

k>1 График функции y=kf(x) получается растяжением графика функции y=f(x) вдоль оси y в k раз.

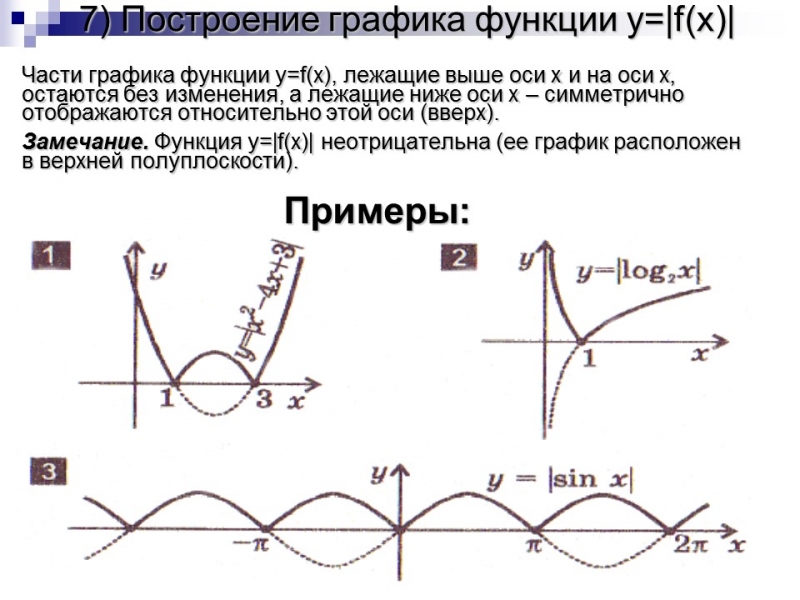
7) Построение графика функции y=|f(x)|

Части графика функции y=f(x), лежащие выше оси x и на оси x, остаются без изменения, а лежащие ниже оси x – симметрично отображаются относительно этой оси (вверх).

Замечание. Функция y=|f(x)| неотрицательна (ее график расположен в верхней полуплоскости).

8) Построение графика функции y=f(|x|)

Часть графика функции y=f(x), лежащая левее оси y, удаляется, а часть, лежащая правее оси y – остается без изменения и, кроме того, симметрично отражается относительно оси y (влево). Точка графика лежащая на оси y, остается неизменной.

Замечание. Функция y=f(|x|) четная (ее график симметричен относительно оси y).

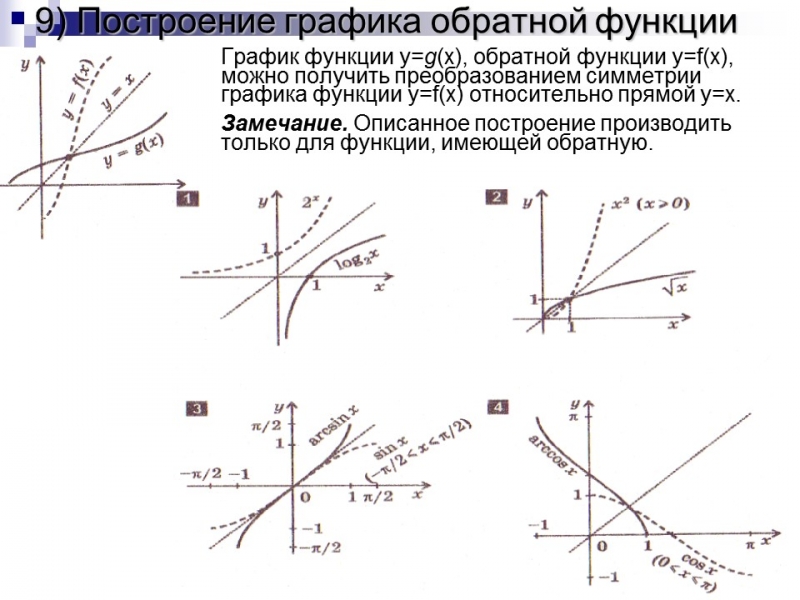
9) Построение графика обратной функции

График функции y=g (x), обратной функции y=f(x), можно получить преобразованием симметрии графика функции y=f(x) относительно прямой y=x.

Замечание. Описанное построение производить только для функции, имеющей обратную.

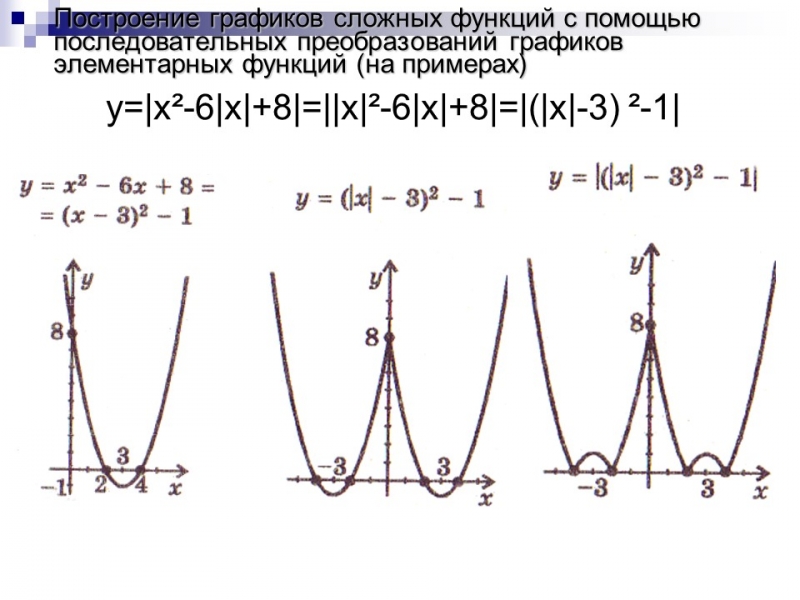
Построение графиков сложных функций с помощью последовательных преобразований графиков элементарных функций (на примерах)

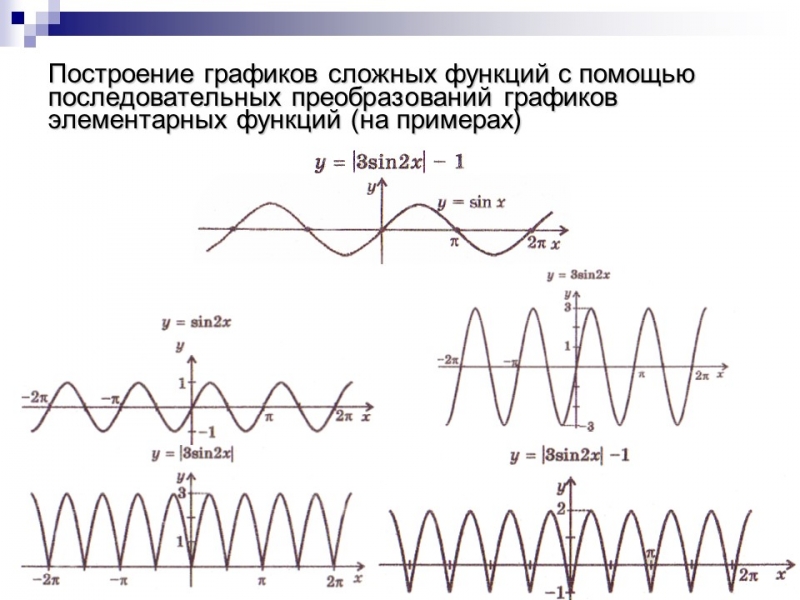
Построение графиков сложных функций с помощью последовательных преобразований графиков элементарных функций (на примерах)

Построение графиков сложных функций с помощью последовательных преобразований графиков элементарных функций (на примерах)

Построение графиков сложных функций с помощью последовательных преобразований графиков элементарных функций (на примерах)

Применение правил преобразования графиков при решении заданий ЕГЭ
(части C).

Решить систему уравнений:

В одной системе координат, построим графики функций: а)

Решить уравнение: f(g(x))+g(f(x))=32 , если известно, что и

Решение : Преобразуем функцию f(x).

Так как , то

Тогда g(f(x))=20.

Подставим в уравнение f(g(x))+g(f(x))=32, получим f(g(x))+20=32;

f(g(x))=12

Пусть g(x)=t, тогда f(t)=12 или

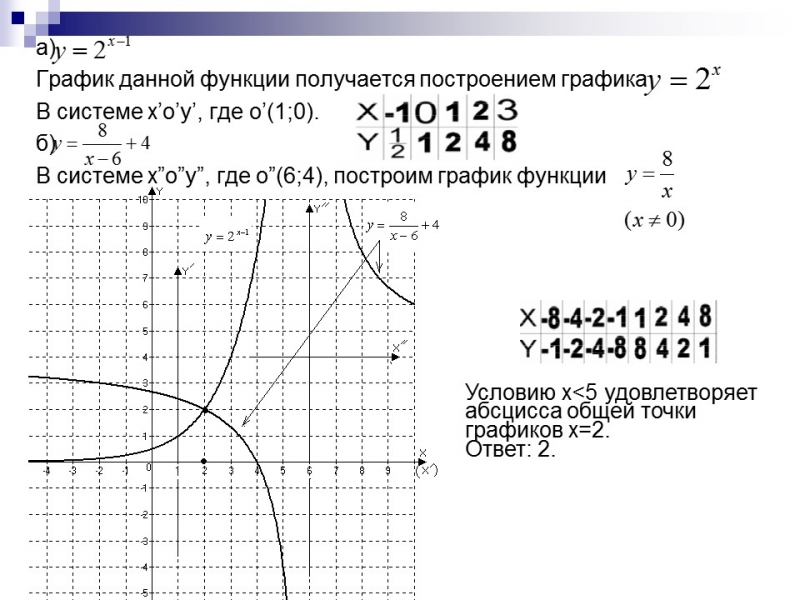
а)

График данной функции получается построением графика

В системе x’o’y’, где o’(1;0).

б)

В системе x”o”y”, где o”(6;4), построим график функции

Вывод:

Мы видим, что правила преобразования графиков существенно упрощают построение графиков сложных функций.

Помогают найти нетрадиционное решение сложных задач.

Тема: « Преобразование графиков функции »