Название: Способы отбора статистических данных
Вид работы: сочинение
Рубрика: Математика
Размер файла: 19.29 Kb
Скачать файл: referat.me-215191.docx
Краткое описание работы: Составление характеристики непрерывного признака. Методы составления приближенного распределения признака, имеющего непрерывное распределения. Относительные частоты и их плотности. Статистическое распределение частот интервального вариационного ряда.
Способы отбора статистических данных
Способы отбора статистических данных
Цель работы:
1. Овладение различными способами отбора статистических данных.
2. Приобретение навыка составление общей характеристики не прерывного признака X.
3. Овладение методами составления приближенного распределения признака X, имеющего непрерывное распределения.
Ход работы:
1. Размер ноги студентов КПиП 2 курса.
2. Социологическое исследование путем проведения сплошного опроса студентов, обучающихся в двух группах.
3. Таблица рассматриваемого признака X:
- размах варьирования:
R = xmax – xmin
Xmax = 46; Xmin = 35
R = 46 – 35 = 11
- размах варьирования R разбили на k частных интервалов, число которых выбирается из условия k ≈ √n.
n = 39
√n ≈ 6,24; k ≈ 6,24, тогда длина частичного интервала
l ≈ R/k; l ≈ 11/6,24; l ≈ 1,76
- статистическое распределение частот интервального вариационного ряда признака X:
| 35 -37 |
37 - 39 |
39 - 41 |
41 - 43 |
43 - 45 |
45 - 47 |
| 5 |
15 |
6 |
3 |
7 |
3 |
- вычислим:
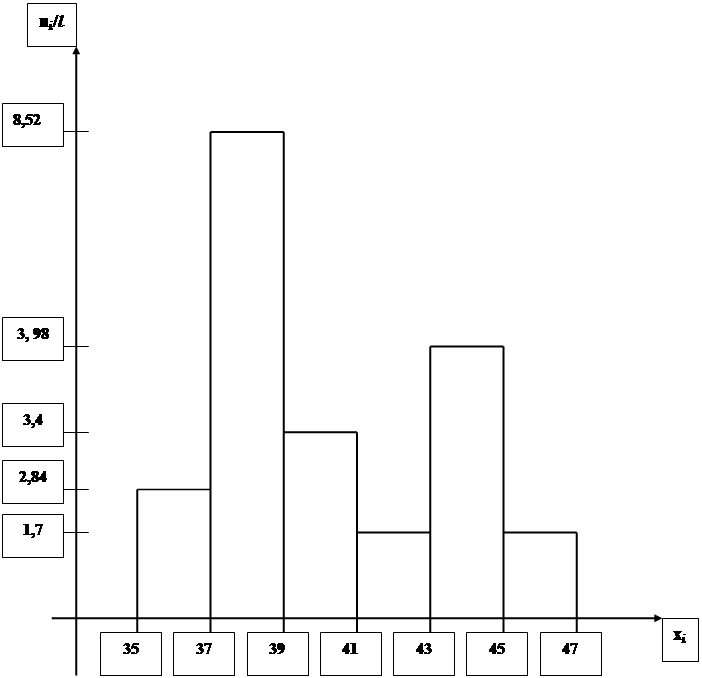
а) плотность частоты ni/l каждого интервала
1) n1/l = 5/1,76 = 2,84
2) n2/l = 15/1,76 = 8,52
3) n3/l = 6/1,76 = 3,4
4) n4/l = 3/1,76 = 1,7
5) n5/l = 7/1,76 = 3,98
6) n6/l = 3/1,76 = 1,7
б) Относительные частоты и плотности относительных частот.
Wi = ni/n
n = 39/39
W1 = n1/n = 5/39 = 0,13
W2 = 15/39 = 0,38
W3 = 6/39 = 0,15
W4 = 3/39 = 0,07
W5 = 7/39 = 0,18
W6 = 3/39 = 0,07
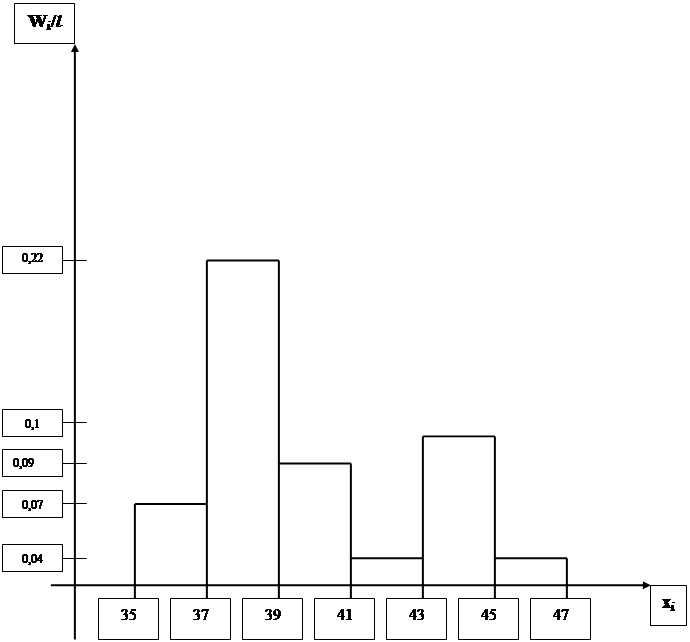
Плотность относительных частот
Wi/l;
W1 = 0,13/1,76 = 0,07
W2 = 0,38/1,76 = 0,22
W3 = 0,15/1,76 = 0,09
W4 = 0,04/1,76 = 0,04
W5 = 0,1/1,76 = 0,1
W6 = 0,04/1,76 = 0,04
| № i |
xi≤x<xi+1 |
ni |
Ni/l |
Wi |
Wi/l |
| 1 2 3 4 5 6 |
35 -37 37 - 39 39 - 41 41 - 43 43 - 45 45 - 47 |
5 15 6 3 7 3 |
2,84 8,52 3,4 1,7 3,98 1,7 |
0,13 0,38 0,15 0,07 0,18 0,07 |
0,07 0,22 0,09 0,04 0,1 0,04 |
4)
5) Статистическое распределение частот дискретного вариационного ряда.
Xi +Xi+1/2
1) 35 + 37 / 2 = 36
2) 37 + 39 / 2 = 38
3) 39 + 41 / 2 = 40
4) 41 + 43 / 2 = 42
5) 43 + 45 / 2 = 44
6) 45 + 47 / 2 = 46
| Xi |
36 |
38 |
0 |
4 |
46 |
44 |
| ni |
5 |
15 |
6 |
3 |
7 |
3 |
Найдем выборочную среднюю и среднеквадратическое отклонение:
XB = 1/n (x1 n1 + x2 n2 + ... + xk nk)
![]() XB
XB![]() = 1/39 ( 36*5 + 38*15 + 40*6 + 42*3 + 44*7) =
= 1/39 ( 36*5 + 38*15 + 40*6 + 42*3 + 44*7) =
= 1/39 (180 + 570 +240 + 126 + 308 +138) = 1562/39 = 40
δ = √ Дв
k
Дв = 1/n ∑ ( Xi – XB)² ni
i = 1
Дв = 1/39 ((36 – 39)² 5 + (38 – 39)² 15 + (40 -39)² 6 + (42 – 39)² 3 + (44 – 39)² 7 +
+ (46 – 39)² 3) =45 + 15 + 6 + 27 + 175 + 147/39 = 415/39 = 10,64
Министерство Российской Федерации
Высшее профессиональное учреждение
Шадринский Государственный Педагогический Институт
Курганская область.
Способы отбора статистических данных
Исследовательская работа
по математике
Выполнили
студенты 255 группы:
Преподаватель:
Щадринск, 2007
Похожие работы
-
Проверка статистической гипотезы о нормальном законе распределения случайной величины
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОУ ВПО ТОмский ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ЭКОЛОГО-ГЕОГРАФИЧЕСКИЙ ФАКУЛЬТЕТ КАФЕДРА КАРТОГРАФИИ И ГИС Лабораторная работа №3
-
Оценивание параметров и проверка гипотез о нормальном распределении
Оценивание параметров и проверка гипотез о нормальном распределении Расчетная работа Выполнил Шеломанов Р.Б. Кафедра математической статистики и эконометрики
-
Основы математики
Задание № 1 В урне 5 белых и 4 черных шара. Из нее вынимают подряд два ряда шара. Найти вероятность того, что оба шара белые. Решение: Всего возможно . (это общее количество возможных элементарных исходов испытания). Интересующая нас событие заключается в том, что данная выборка содержит 2 белых шара, подсчитаем число благоприятствующих этому событию вариантов:
-
Вариационные ряды
Задание № 1. По данной выборке: а) Найти вариационный ряд; б) Построить функцию распределения; в) Построить полигон частот; г) Вычислить среднее значение СВ, дисперсию, среднеквадратичное отклонение.
-
Статистические величины
Сущность и значение средних величин. В результате группировки единиц совокупности по величине варьирующего признака получают ряды распределения - первичную характеристику массовой статистической совокупности. Чтобы охарактеризовать такую совокупность в целом, часто пользуются средней величиной.
-
Проверка гипотезы о законе распределения генеральной совокупности X по критерию Пирсона
Федеральное агентство по образованию РФ Сибирская государственная автомобильно-дорожная академия (СибАДИ) Кафедра: «Высшая математика» РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА
-
Методика обработки экспериментальных данных 2
Задание на курсовую работу Построить вариационный ряд Рассчитать числовые характеристики статистического ряда: а) Размах варьирования. б) Среднее арифметическое значение.
-
Средние величины 3
Тема 5. СРЕДНИЕ ВЕЛИЧИНЫ 5.1. Понятие о средней величине Средняя величина является обобщающей количественной характеристикой изучаемого признака в исследуемой совокупности. В статистике используются различного рода средние величины.
-
Исследование прочности на разрыв полосок ситца
Задачи математической статистики. Распределение случайной величины на основе опытных данных. Эмпирическая функция распределения. Статистические оценки параметров распределения. Нормальный закон распределения случайной величины, проверка гипотезы.
-
Основы теории вероятностей
Закон распределения случайной величины Х, функция распределения и формулы основных числовых характеристик: математическое ожидание, дисперсия и среднеквадратичное отклонение. Построение полигона частот и составление эмпирической функции распределения.