Referat.me
/ / Основы теории вероятностей

Название: Основы теории вероятностей

Вид работы: контрольная работа

Рубрика: Математика

Размер файла: 36.62 Kb

Скачать файл: referat.me-215150.docx

Краткое описание работы: Закон распределения случайной величины Х, функция распределения и формулы основных числовых характеристик: математическое ожидание, дисперсия и среднеквадратичное отклонение. Построение полигона частот и составление эмпирической функции распределения.

Основы теории вероятностей

Вариант 2

1. Решите уравнение

Решение:

По определению .

Тогда и уравнение принимает вид откуда получаем .

Ответ: .

2. В урне находится 7 белых и 5 черных шаров. Найти вероятность того, что два одновременно изъятых шара будут белыми.

Решение:

Изначально в урне 12 шаров и вероятность извлечь первый шар белый составляет . После того как извлечен первый белый шар в урне остается 11 шаров, из них 6 белых, следовательно вероятность извлечь второй белый шар составит .

В итоге вероятность совместного появления двух белых шаров равна:

Ответ: .

3. В ящике 10 деталей, из которых 4 стандартные. Контролер взял наудачу 3 детали. Найти вероятность того, что хотя бы одна из изъятых деталей окажется стандартной.

Решение:

События «хотя бы одна стандартная» и «все детали не стандартные» противоположны и сумма их вероятностей равна 1.

Найдем вероятность того, что 3 извлеченных детали не стандартные.

Общее число возможных элементарных исходов выбора 3-х деталей из 10 равно числу сочетаний из 10 элементов по 3: , где , тогда

Определим число исходов, благоприятствующих интересующему нас событию А (среди 3-х выбранных деталей 3 не стандартных). Три детали из 6 имеющихся можно выбрать способами следовательно, число благоприятствующих исходов .

Искомая вероятность равна отношению числа исходов, благоприятствующих нужному событию, к числу всех элементарных исходов: .

Тогда искомая вероятность того, что хотя бы одна из изъятых деталей окажется стандартной равна:

Ответ: .

4. В коробке 7 карандашей, из которых 4 красные. Из этой коробки наудачу извлекается 3 карандаша. Х – число красных карандашей. Найти закон распределения случайной величины Х, функцию распределения и основные числовые характеристики.

Решение:

Среди 3-х извлеченных карандашей может быть 0, 1, 2 или 3 красных.

Найдем вероятность каждого исхода.

0 красных:

1 красный:

2 красных:

3 красных:

Закон распределения принимает вид:

Х 0 1 2 3
р

Запишем функцию распределения полученной случайной величины Х:

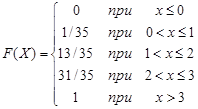
Математическое ожидание М(Х) дискретной случайной величины находится по формуле:

,

и подставляя данные получим:

Дисперсию дискретной случайной величины можно вычислить по формуле:

,

и, подставляя данные, получим:

Среднеквадратичное отклонение: s(Х)=

Ответ: ;;

5. По данной выборке постройте полигон. Найти эмпирическую функцию.

Хi 4 7 8
Ni 5 2 3

Решение:

Построим полигон частот – ломаную, соединяющую точки с координатами (Хi; Ni).

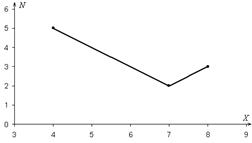
Объем выборки равен N = 5 + 2 + 3 = 10.

Найдем относительные частоты и составим эмпирическую функцию распределения:

Хi 4 7 8
wi 0,5 0,2 0,3

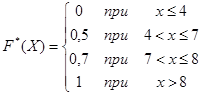
Ответ: решение выше.

Похожие работы

  • Шпаргалка по Теории Вероятности

    1) свойство вероятности: 20 стр. Свойство 1. Вероятность невозможного события равна 0, т.е. Свойство 2. Вероятность достоверного события равна 1, т.е.

  • Ряд распределения функция распределения

    Задача 1 (5) Производится контроль партии из 4 изделий. Вероятность изделия быть неисправным равна 0,1. Контроль прекращается при обнаружении первого неисправного изделия. Х – число обследованных приборов. Найти:а) ряд распределения Х б)функцию распределения F(X), в ответ ввести F(3.5). в) m(x) г) d(x) д) p(1.5<X<3.5).

  • Задачи и примеры их решения по теории вероятности

    Вариант 3. 1. Решите уравнение Решение По определению Тогда и уравнение принимает вид откуда получаем Так как m может быть только натуральным числом, то значение

  • Основы математики

    Задание № 1 В урне 5 белых и 4 черных шара. Из нее вынимают подряд два ряда шара. Найти вероятность того, что оба шара белые. Решение: Всего возможно . (это общее количество возможных элементарных исходов испытания). Интересующая нас событие заключается в том, что данная выборка содержит 2 белых шара, подсчитаем число благоприятствующих этому событию вариантов:

  • Вариационные ряды

    Задание № 1. По данной выборке: а) Найти вариационный ряд; б) Построить функцию распределения; в) Построить полигон частот; г) Вычислить среднее значение СВ, дисперсию, среднеквадратичное отклонение.

  • Методика обработки экспериментальных данных 2

    Задание на курсовую работу Построить вариационный ряд Рассчитать числовые характеристики статистического ряда: а) Размах варьирования. б) Среднее арифметическое значение.

  • Теория вероятности и математическая статистика

    Особенности выполнения теоремы Бернулли на примере электрической схемы. Моделирование случайной величины по закону распределения Пуассона, заполнение массива. Теория вероятности, понятие ожидания, дисперсии случайной величины и закон распределения.

  • Исследование прочности на разрыв полосок ситца

    Задачи математической статистики. Распределение случайной величины на основе опытных данных. Эмпирическая функция распределения. Статистические оценки параметров распределения. Нормальный закон распределения случайной величины, проверка гипотезы.

  • Задачи по Математике

    ЗАДАЧИ КОНТРОЛЬНОЙ РАБОТЫ Задачи № 1-10. Решить систему линейных алгебраических уравнений тремя способами: 1) методом Крамера, 2) с помощью обратной матрицы, 3) методом Гаусса.

  • Вычисление случайных величин

    Задача №1. Двумерная случайная величина (X,Y) имеет равномерное распределение вероятностей в треугольной области ABC: где S – площадь треугольника ABC.