Название: Экономико-математическое моделиpование
Вид работы: реферат
Рубрика: Математика
Размер файла: 196.32 Kb
Скачать файл: referat.me-215433.docx
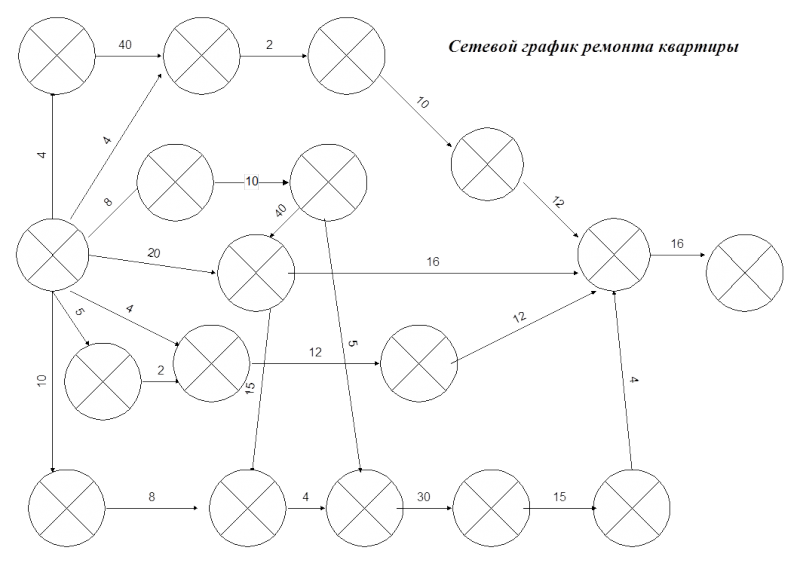
Краткое описание работы: ЗАДАЧА №2 Построить сетевую модель ремонта Вашей квартиры а) определить критический путь б) рассчитать поздние сроки окончания и начала событий в) рассчитать ранние сроки окончания и начала событий
Экономико-математическое моделиpование
ЗАДАЧА №2
Построить сетевую модель ремонта Вашей квартиры
а) определить критический путь
б) рассчитать поздние сроки окончания и начала событий
в) рассчитать ранние сроки окончания и начала событий
г) рассчитать резервы событий
Решение:
- Делаем ремонт двухкомнатной квартиры улучшенной планировки: жилая комната, детская, кухня, ванна, туалет и коридор.
2. Необходимо сделать:
· сменить обои во всех помещениях;
· покрасить окна;
· в зале и коридоре сделать подвесные потолки с рассеяным светом
· в оттальных помещениях потолок покрывается краской КЧ
· покрасить входную дверь;
· постелить по всей квартире линолиум
3. Строим таблицу ремонта и сетевой график
4."Четырехсекторным" методом рассчитываем параметры сетевого графика и определяем "критический путь".
5. Расчитываем параметры сетевого графика и резервы времени
| ЗА ДАЧА 1 | ||||||
| Условие задачи: | ||||||
| В табице приведены показатели коэффициентов прямых затрат и | ||||||
| объемы конечных продуктов трех взаимосвязанных отраслей | ||||||
| Рассчитать: | ||||||
| 1) Валовые выпуски отраслей | ||||||
| 2) объемы межотраслевых поставок | ||||||
| 3) матрицу полных затрат итерационным методом, ограничившись | ||||||
| уровнем косвенных затрат третьего порядка | ||||||
| Произво-дящие отрасли | Коэффициенты прямых затрат Потребляющие отрасли | Конечный продукт Yi | ||||
| 1 | 2 | 3 | ||||
| 1 | 0,2 | 0,1 | 0,005 | 100 | ||
| 2 | 0,15 | 0,1 | 0,25 | 100 | ||
| 3 | 0,3 | 0,05 | 0,1 | 200 | ||
| Р е ш е н и е | ||||||
| 1. Валовый выпуск отраслей находим по формуле: | ||||||
| X = ( E - A )-1 * Y ( 1 ) | ||||||
| 1.1 Найдем матрицу ( E - A ) | ||||||
| (E-А) | 0,8 | -0,1 | -0,005 | |||
| -0,15 | 0,9 | -0,25 | ||||
| -0,3 | -0,05 | 0,9 | ||||
| 1.2 Найдем элементы обратной матрицы ( E - A )-1 | ||||||
| D= | 0,615613 | детерминант матрицы (Е-А) | ||||
| Алгебраические дополнения каждого элемента матрицы (Е-А): | ||||||
| a11= | 0,80 | |||||
| a12= | 0,21 | |||||
| a13= | 0,28 | |||||
| a21= | 0,09 | |||||
| a22= | 0,72 | |||||
| a23= | 0,07 | |||||
| a31= | 0,03 | |||||
| a32= | 0,20 | |||||
| a33= | 0,71 | |||||
|
Y | |||||
| (E-A)-1 = | 1,299519 | 0,1462 | 0,04792 |
|
||
| 0,341124 | 1,1671 | 0,3261 | 100 | |||
| 0,454832 | 0,1137 | 1,1452 | 200 | |||
| 1.4 определим валовый выпуск продукции в каждой отрасли | ||||||
| по формуле X=(E-А)-1*Y | ||||||
| Х1= | 154,16 | |||||
| Х2= | 216,04 | |||||
| Х3= | 285,89 | |||||
| 2. Найдем объемы межотраслевых поставок | ||||||
| xij =aij *Xj, где Xj - валовый продукт j отрасли, а aij - прямые затраты | ||||||
| матрица межотраслевых поставок: | ||||||
|
30,83 | 15,42 |
|
|||
| Мij= | 32,41 | 21,60 | 54,01 | |||
| 85,77 | 14,29 | 28,59 | ||||
| 3) Найдем полные затраты итерационным методом | ||||||
| Как известно, чтобы получить матрицу косвенных затрат первого | ||||||
| порядка надо матрицу прямых затрат Аij умножить саму на себя | ||||||
| Каждый элемент матрицы косвенных затрат первого порядка можно | ||||||
| найти по формуле: | aij(1) = å | aik*akj | ||||
|
0,0303 | 0,0265 | ||||
| Аij(1) = | 0,12 | 0,0375 | 0,05075 | |||
| 0,0975 | 0,04 | 0,024 | ||||
| Чтобы получить матрицу косвенных затрат второго порядка, нужно | ||||||
| матрицу прямых затрат умножить справа на матрицу косвенных затрат | ||||||
| первого порядка | ||||||
| Аij(2) = | Аij * | Аij(1) | ||||
| Каждый элемент матрицы косвенных затрат второго порядка можно | ||||||
| найти по формуле: | aij(2) = å | aik*akj(1) | ||||
| Итак матрица косвенных затрат второго порядка: |
|
|||||
|
0,023788 | 0,01 | 0,0105 | |||
| Аij(2) = | 0,04485 | 0,0183 | 0,01505 | |||
| 0,0327 | 0,015 | 0,01289 | ||||
| матрица косвенных затрат третьего порядка: | ||||||
|
0,009406 | 0,0039 | 0,00367 |
|
||
| Аij(3) = | 0,016228 | 0,0071 | 0,0063 | |||
| 0,012649 | 0,0054 | 0,01289 | ||||
| Матрица полных затрат : | ||||||
|
0,289694 | 0,1442 | 0,04566 | |||
| 0,331078 | 0,1629 | 0,3221 | ||||
| 0,442849 | 0,1104 | 0,14978 | ||||
Ремонт. Задача 2
| Работа | Содержание работы | Длитель-ность, часы |
| Кухня | ||
| 0-1 | Удаление старых обоев | 4 |
| 1-2 | Оклейка кафельной плиткой | 40 |
| 0-2 | Окраска оконных рам | 4 |
| 2-3 | Потолок покрывается краской КЧ | 2 |
| 3-4 | Оклейка обоями | 10 |
| Зал | ||
| 0-5 | Удаление старых обоев в жилой комнате, подготовка стен(затираем неровности, покрываем клеем) | 8 |
| 5-6 | Работа с электропроводкой | 10 |
| 0-7 | Подготовка (удаление старой краски, шлифовка) и окраска оконных рам | 20 |
| 6-7 | Изготовление подвесного потолка | 40 |
| 7-12 | Оклейка обоями | 15 |
| Детская комната | ||
| 0-8 | Удаление старых обоев в детской | 5 |
| 8-9 | Потолок покрывается краской КЧ | 2 |
| 0-9 | Окраска оконных рам | 4 |
| 9-10 | Оклейка обоями | 12 |
| Ванная и туалет | ||
| 0-11 | Красим ванную | 10 |
| 11-12 | Красим туалет | 8 |
| Коридор | ||
| 12-13 | Удаление старых обоев | 4 |
| 6-13 | Работа с электропроводкой | 5 |
| 13-14 | Изготовление подвесного потолка | 30 |
| 14-15 | Оклейка обоями | 15 |
| 15-16 | Покраска входной двери | |
| Линолиум по всей квартире | ||
| 7-16 | Линолиум в зале | 16 |
| 10-16 | Линолиум в детской | 12 |
| 4-16 | Линолиум в кухне | 12 |
| 16-17 | Линолиум в коридоре | 16 |
Таблица ко 2 задаче
| Параметры сетевого графика и резерв | |||||||||||
| i | j | tij | Tj ран | Ti ран | Tj позд | Ti позд | tij | tij | tij | tij | Rij |
| раннее начало | раннее окончание | позднее окончание | позднее начало | резерв | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 0 | 1 | 4 | 4 | 0 | 62 | 0 | 0 | 4 | 62 | 58 | 58 |
| 1 | 2 | 40 | 44 | 4 | 102 | 62 | 4 | 44 | 102 | 62 | 58 |
| 0 | 2 | 4 | 44 | 0 | 102 | 0 | 0 | 4 | 102 | 98 | 58 |
| 2 | 3 | 2 | 46 | 44 | 104 | 102 | 44 | 46 | 104 | 102 | 58 |
| 3 | 4 | 10 | 56 | 46 | 114 | 104 | 46 | 56 | 114 | 104 | 58 |
| 4 | 16 | 12 | 126 | 56 | 126 | 114 | 56 | 68 | 126 | 114 | 0 |
| 0 | 5 | 8 | 8 | 0 | 8 | 0 | 0 | 8 | 8 | 0 | 0 |
| 5 | 6 | 10 | 18 | 8 | 18 | 8 | 8 | 18 | 18 | 8 | 0 |
| 0 | 7 | 20 | 58 | 0 | 58 | 0 | 0 | 20 | 58 | 38 | 0 |
| 6 | 7 | 40 | 58 | 18 | 58 | 18 | 18 | 58 | 58 | 18 | 0 |
| 6 | 13 | 5 | 77 | 18 | 77 | 18 | 18 | 23 | 77 | 72 | 0 |
| 7 | 12 | 15 | 73 | 58 | 73 | 58 | 58 | 73 | 73 | 58 | 0 |
| 7 | 16 | 16 | 126 | 58 | 126 | 58 | 58 | 74 | 126 | 110 | 0 |
| 0 | 8 | 5 | 5 | 0 | 100 | 0 | 0 | 5 | 100 | 95 | 95 |
| 0 | 9 | 4 | 7 | 0 | 102 | 0 | 0 | 4 | 102 | 98 | 95 |
| 8 | 9 | 2 | 7 | 5 | 102 | 100 | 5 | 7 | 102 | 100 | 95 |
| 9 | 10 | 12 | 19 | 7 | 114 | 102 | 7 | 19 | 114 | 102 | 95 |
| 10 | 16 | 12 | 126 | 114 | 126 | 114 | 114 | 126 | 126 | 114 | 0 |
| 0 | 11 | 10 | 10 | 0 | 65 | 0 | 0 | 10 | 65 | 55 | 55 |
| 11 | 12 | 8 | 73 | 10 | 73 | 65 | 10 | 18 | 73 | 65 | 0 |
| 12 | 13 | 4 | 77 | 73 | 77 | 73 | 73 | 77 | 77 | 73 | 0 |
| 13 | 14 | 30 | 107 | 77 | 107 | 77 | 77 | 107 | 107 | 77 | 0 |
| 14 | 15 | 15 | 122 | 107 | 122 | 107 | 107 | 122 | 122 | 107 | 0 |
| 15 | 16 | 4 | 126 | 122 | 126 | 122 | 122 | 126 | 126 | 122 | 0 |
| 16 | 17 | 16 | 142 | 126 | 142 | 126 | 126 | 142 | 142 | 126 | 0 |
Задача 3
| х1 | х2 |
| 0 | 50 |
| 0,1 | 26,11 |
| 0,2 | 18,48 |
| 0,3 | 12,93 |
| 0,4 | 8,411 |
| 0,5 | 4,529 |
| 0,6 | 1,088 |
| 0,7 | -2,02 |
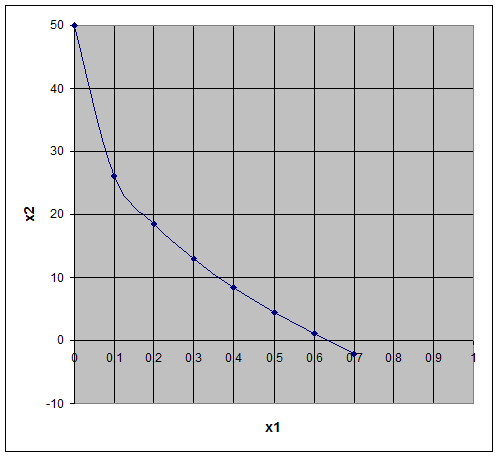
График №3
| З А Д АЧА 4 | ||||||||||
| Условие задачи. | ||||||||||
| Задана следующая экономическая ситуация. Завод выпускает изделия двух | ||||||||||
| типов А и В. При этом используется сырье четырех видов. Расход | ||||||||||
| сырья каждого вида на изготовление еденицы продукции и запасы сырья | ||||||||||
| заданы в таблице | ||||||||||
| Изделия | Сырье | |||||||||
| 1 | 2 | 3 | 4 | |||||||
| А | 2 | 1 | 0 | 2 | ||||||
| В | 3 | 0 | 1 | 1 | ||||||
| Запасы сырья | 21 | 4 | 6 | 10 | ||||||
| Выпуск изделия А приносит 3 денежные еденицы, В - 2 денежные единицы. | ||||||||||
| Составить план производства, обеспечивающий максимальную | ||||||||||
| прибыль | ||||||||||
| а) составьте матиматическую модель задачи; | ||||||||||
| б) поясните смысл целевой функции и ограничении | ||||||||||
| Решение: | ||||||||||
| а) Математическая модель | ||||||||||
| 2x1+3x2 <=21 | ||||||||||
| x1 <=4 | ||||||||||
| x2+ <=6 | ||||||||||
| 2x1+ x2 <=10 | ||||||||||
| x1 >=0 | ||||||||||
| x2 >=0 | ||||||||||
| б) Суммарный расход каждого вида сырья на весь выпуск не должен | ||||||||||
| превышать заданного ограничения. | ||||||||||
| Валовая реализация (сумма объемов реализации по каждому виду | ||||||||||
| продукции в денежном выражении) должна стремиться при заданных | ||||||||||
| условиях к максиму | ||||||||||
| в) Решать будем симплекс методом | ||||||||||
| преобразуем неравенства в равенства, для этого введем четыре | ||||||||||
| дополнительные переменные | ||||||||||
| 2x1+3x2+ x3 =21 | ||||||||||
| x1 + x4 =4 | ||||||||||
| x2 +x5 =6 | ||||||||||
| 2x1+x2+ x6 =10 | ||||||||||
| f=3x1+2x2+0*x3+0*x4+0*x5+0*x6 -> max | ||||||||||
| перепишем в виде систем 0 уравнений | ||||||||||
| 0= 21-(2x1+3x2+x3) | ||||||||||
| 0= 4-( x1 + x4) | ||||||||||
| 0= 6-( x2+ х5) | ||||||||||
| 0=10-(2х1+х2+ х6) | ||||||||||
| f=0-(-3x1-2x2-0*x3-0*x4-0*x5-0*x6) | ||||||||||
| Система уравнений может быть записана в виде векторного равенства | ||||||||||
| 0=В - (А1х1+А2х2+А3х3+А4х4+А5х5+А6х6) | ||||||||||
| В - свободные члены | ||||||||||
| А1…А6 коэффициенты при переменных х1…х6 | ||||||||||
| Линейная форма имеет вид : f=c1x1+c2x2+c3x3+c4x4+c5x5+c6x6 | ||||||||||
| Векторы А3,А4, А5,А6 составляют базис | ||||||||||
| Составляем первую симплекс таблицу | ||||||||||
| Базисный вектор | Коэф.лин. формы с | вектор св. член b | b/a | 3 A1 | 2 A2 | 0 A3 | 0 A4 | 0 A5 | 0 A6 | |
| А3 | 0 | 21 | 10,5 | 2 | 3 | 1 | 0 | 0 | 0 | |
|
0 | 4 | 4 | 1 | 0 | 0 | 1 | 0 | 0 | |
| A5 | 0 | 6 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | |
| A6 | 0 | 10 | 5 | 2 | 1 | 0 | 0 | 0 | 1 | |
| индексная строка fj-сj | 0 | -3 | -2 | |||||||
| Решение: | х1=0,х2=0,х3=21,х4=4,х5=6,х6=10 | |||||||||
| f=0 | ||||||||||
| Так как в индексной строке есть отрицательные элементы -решение не | ||||||||||
| является оптимальным. | ||||||||||
| A1 вводим в базис вместо вектора А4 | ||||||||||
| Базисный вектор | Коэф.лин. формы с | вектор св. член b | b/a | 3 A1 | 2 A2 | 0 A3 | 0 A4 | 0 A5 | 0 A6 | |
| A3 | 0 | 13 | 4 1/3 | 0 | 3 | 1 | -2 | 0 | 0 | |
| A1 | 3 | 4 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | |
| А5 | 0 | 6 | 6 | 0 | 1 | 0 | 0 | 1 | 0 | |
|
0 | 2 | 2 | 0 | 1 | 0 | -2 | 0 | 1 | |
| индексная строка fj-сj | 0 | -2 | 0 | 3 | 0 | 0 | ||||
| Решение: | х1=4,х2=0,х3=13,х4=0,х5=6,х6=2 | |||||||||
| f=12 | ||||||||||
| Так как в индексной строке есть отрицательные элементы -решение не | ||||||||||
| является оптимальным. | ||||||||||
| A2 вводим в базис вместо вектора А6 | ||||||||||
| Базисный вектор | Коэф.лин. формы с | вектор св. член b | b/a | 8 A1 | 7 A2 | 6 A3 | 0 A4 | 0 A5 | 0 A6 | |
|
0 | 7 | 1 3/4 | 0 | 0 | 1 | 4 | 0 | -3 | |
| A1 | 3 | 4 | 4 | 1 | 0 | 0 | 1 | 0 | 0 | |
| А5 | 0 | 4 | 2 | 0 | 0 | 0 | 2 | 1 | -1 | |
| A2 | 2 | 2 | -1 | 0 | 1 | 0 | -2 | 0 | 1 | |
| индексная строка fj-сj | 0 | 0 | 0 | -1 | 0 | 2 | ||||
| Решение: | x1=4, x2=2; x3=7; x4=0;x5=4;x6=0 | |||||||||
| f=12 | ||||||||||
| Так как в индексной строке есть отрицательные элементы -решение не | ||||||||||
| является оптимальным. | ||||||||||
| A4 вводим в базис вместо вектора А3 | ||||||||||
| Базисный вектор | Коэф.лин. формы с | вектор св. член b | b/a | 8 A1 | 7 A2 | 6 A3 | 0 A4 | 0 A5 | 0 A6 | |
| A4 | 0 | 1 3/4 | 0 | 0 | 1/4 | 1 | 0 | - 3/4 | ||
| A1 | 3 | 2 1/4 | 1 | 0 | - 1/4 | 0 | 0 | 3/4 | ||
| А5 | 0 | 1/2 | 0 | 0 | - 1/2 | 0 | 1 | 1/4 | ||
| A2 | 2 | 5 1/2 | 0 | 1 | 1/2 | 0 | 0 | -1 1/2 | ||
| индексная строка fj-сj | 0 | 0 | 1/4 | 0 | 0 | 1 1/4 | ||||
| Решение: | x1=2,25, x2=5,5; x3=0; x4=1 3/4;x5=1/2;x6=0 | |||||||||
| f=17,75 | ||||||||||
| В индексной строке нет отрицательных элементов, следовательно | ||||||||||
| дальнейшее увеличение значения линейной формы невозможно мы получили | ||||||||||
| оптимальную программу | ||||||||||
| Максимальная прибыль достигается при изготовлении первого вида | ||||||||||
| продукции 2,25 у.е., а второго 5,5 у.е. | ||||||||||
| Так как нам не было задано условие целочисленности, такие значения | ||||||||||
| допустимы, например в качестве условных едениц - тысячи тонн. | ||||||||||
| ЗАДАЧА 5 | ||||||||
| Наити максимум функции F при заданных ограничениях | ||||||||
| F = x1+2x2 ->max | ||||||||
| 3x1+x2 >=3 | (1) | |||||||
| 3x1-x2 <=0 | (2) | |||||||
| x1-x2 >=3 | (3) | |||||||
| x1>=0 | (4) | |||||||
| x2>=0 | (5) | |||||||
| Решить графическим методом | ||||||||
| Решение | ||||||||
| 1.Из условия знакоположительности - первой допустимой областью | ||||||||
| решения является первая четверть декартовой системы координат | ||||||||
| 2. Построим области допустимых значений, для этого построим линии | ||||||||
| для каждого из уравнений | ||||||||
| 3x1+x2 =3 | ||||||||
| 3x1-x2 =0 | ||||||||
| x1-x2 =3 | ||||||||
| и линию для функции f | ||||||||
| x1+2x2 =0 | ||||||||
| 3. Наидем область допустимых значений | ||||||||
| 4. Как видно на графике области допустимых значений для | ||||||||
| ограничении (1),(2) и (3) не пересекаются, значит система не имеет | ||||||||
| допустимых решений. Ограничения противоречивы. | ||||||||
| 5.Для того чтобы система была решаема, она должна быть например | ||||||||
| такой | F = x1+2x2 ->max | |||||||
| 3x1+x2 <=3 | ||||||||
| 3x1-x2 <=0 | ||||||||
| x1-x2 <=3 | ||||||||
| x1>=0 | ||||||||
| x2>=0 | ||||||||
| Тогда область допустимых решений - треугольник АВС | ||||||||
| И функция F достигает максимума в точке С (0;3) и F=6 | ||||||||
| Уравнения | значения | |
| x1 | x2 | |
| для уравнения 3x1+x2=3 | 0 | 3 |
| 2 | -3 | |
| для уравнения 3x1-x2=0 | 0 | 0 |
| 2 | 6 | |
| для уравнения x1-x2=3 | 0 | -3 |
| 5 | 2 | |
| для уравнения x1+2x2=0 | 0 | 0 |
| (линия функции) | 5 | -2,5 |
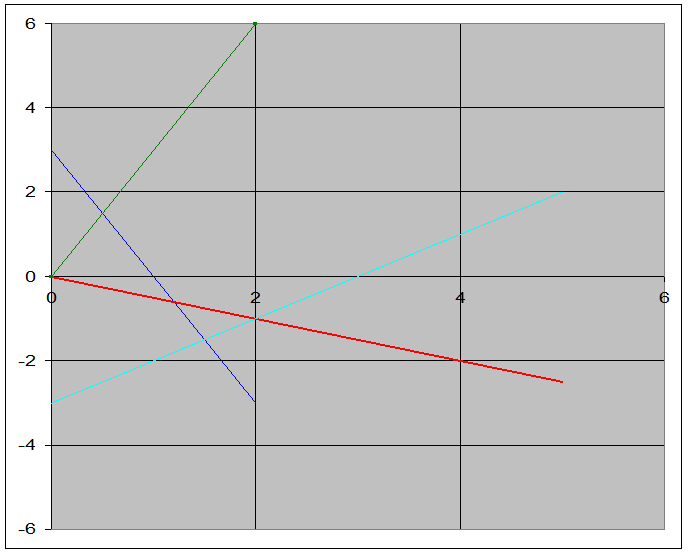
Диаграмма к 5
| ЗАДАЧА 6 | |||||||||||||||||||
| Имеются следующие данные об урожайности зерновых культур Y (в ц/га) | |||||||||||||||||||
| количестве осадков Х1 (в см) выпавших в вегетационный период | |||||||||||||||||||
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||||||||
| Yi | 23 | 24 | 27 | 27 | 32 | 31 | 33 | 35 | 34 | 32 | |||||||||
| Xi | 25 | 27 | 30 | 35 | 36 | 38 | 39 | 41 | 42 | 45 | |||||||||
| Требуется : | |||||||||||||||||||
| а)Определить параметры уравнения регрессии; | |||||||||||||||||||
| б) определить коэффициент парной корреляции и проверить его | |||||||||||||||||||
| статическую надежность | |||||||||||||||||||
| 1. Количественные оценки связи между величинами случайного процесса | |||||||||||||||||||
| устанавливает регрессионный анализ. Связи между переменными могут | |||||||||||||||||||
| линейные и нелинейные. В простейшем случае значения Y выражаются в | |||||||||||||||||||
| виде линейной зависимости : | |||||||||||||||||||
| Y =a + bX, | |||||||||||||||||||
| где a и b - коэффициенты регрессии. | |||||||||||||||||||
| Наиболее часто для расчетов коэффициентов применяют метод | |||||||||||||||||||
| наименьших квадратов. | |||||||||||||||||||
| 2. По методу наименьших квадратов произведем расчет коэффициентов | |||||||||||||||||||
| уравнения регрессии | |||||||||||||||||||
| из системы уравнении | |||||||||||||||||||
| sum(Yi)= n*A + B sum(Xi) | |||||||||||||||||||
| sum(XiYi) = A* sum(Xi) + B*sum(Xi2)) | |||||||||||||||||||
| имеем | |||||||||||||||||||
| А = sum(Yi) * sum(Xi2 ) - sum(XiYi) * sum(Xi) | |||||||||||||||||||
| n* sum(Xi2)- (sum(Xi) 2) | |||||||||||||||||||
| B = n*sum(XiYi) - sum(Xi)* sum(Yi) | |||||||||||||||||||
| n*sum(Xi2)- (sum(Xi))2 | |||||||||||||||||||
| A=S2*S3-S4*S1 B=n*S4-S1*S2, | |||||||||||||||||||
| n*S3-S1*S1 | n*S3-S1*S1 | ||||||||||||||||||
| где S1=SUM(Xi) S2=SUM(Yi) S3=SUM(Xi2 ) | |||||||||||||||||||
| S4=SUM(XiYi) | |||||||||||||||||||
| n - общее число замеров, в нашем случае это 10 | |||||||||||||||||||
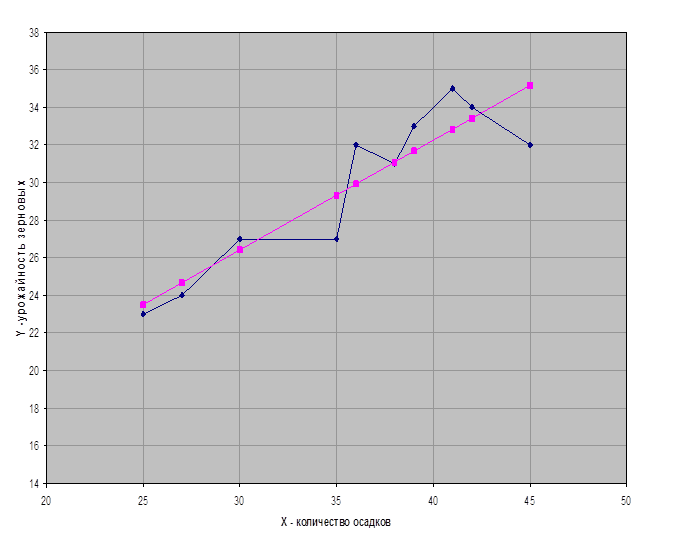
| 2.В результате расчета получено уравнение регрессии: | |||||||||||||||||||
| Y= | 8,917+0,583*Х | ||||||||||||||||||
| 3.Подставив значения X в уравнение найдем Y расчетное. | |||||||||||||||||||
| 4.По значениям экспериментальным и теоретическим строим графики. | |||||||||||||||||||
| 5. Связь между двумя случайными величинами, которая определяется с | |||||||||||||||||||
| некоторой вероятностью, называется корреляционной. Для | |||||||||||||||||||
| количественной оценки линейной корреляции используется коэффициент | |||||||||||||||||||
| парной корреляции | |||||||||||||||||||
| r = 10*S4-S1*S2 | |||||||||||||||||||
| (10*S3-S12 )*(10*S5-S22 ) | |||||||||||||||||||
| S5=SUM(Yi2) | |||||||||||||||||||
| r= | 0,9104 | ||||||||||||||||||
| По таблице Чеддока найдём тесноту связи между двумя явлениями, связь | |||||||||||||||||||
| "очень тесная" | |||||||||||||||||||
| 6.Качество уравнений регрессии оценивают по его прогнозирующей | |||||||||||||||||||
| способности. Уравнения хорошо прогнозируют(т.е. адекватно описывают) | |||||||||||||||||||
| экспериментальные данные, если расхождения между экспериментальными | |||||||||||||||||||
| и расчетными данными находятся в допустимых пределах. | |||||||||||||||||||
| Для проверки адекватности уравнения найдем среднюю относительную | |||||||||||||||||||
| ошибку прогнозирования E: | |||||||||||||||||||
| E=100 *SUM |Yэi - Ypi| | |||||||||||||||||||
| 10 Yэi | |||||||||||||||||||
| где Yэi -экспериментальное, Ypi - расчетное значение | |||||||||||||||||||
| Е= | 4,434% | ||||||||||||||||||
| Это сравнительно большое значение ошибки прогнозирования при | |||||||||||||||||||
| полученном выше значении r. | |||||||||||||||||||
| Внимательно посмотрим на значения отклонений между фактическими и | |||||||||||||||||||
| расчетными значениями Y. Почти непрерывный рост уражайности | |||||||||||||||||||
| после 8 года сменяется спадом. 10 год дает самый большой прирост | |||||||||||||||||||
| ошибки прогнозирования. | |||||||||||||||||||
| По всей видимости, для описания зависимости, лучше подошло бы | |||||||||||||||||||
| не уравнение прямой, а уравнение параболлы, так как после достижения | |||||||||||||||||||
| определенного уровня осадков урожайность начинает падать (много воды - | |||||||||||||||||||
| это тоже плохо для урожая) см. последние значения Х и Y | |||||||||||||||||||
| В 4 год также сравнительно большое расхождение, это может быть | |||||||||||||||||||
| вызванно тем, что урожайность зерновых зависит не только от | |||||||||||||||||||
| количества осадков, но и от многих других факторов, например от | |||||||||||||||||||
| количества теплых дней. Просто было холодно. | |||||||||||||||||||
| i | X | Y | X2 | XY | Yрасч | Y2 | (Y-Yрасч) Y | ||||||||||||
| 1 | 25 | 23 | 625 | 575 | 23,5 | 529 | 0,0217 | ||||||||||||
| 2 | 27 | 24 | 729 | 648 | 24,67 | 576 | 0,0279 | ||||||||||||
| 3 | 30 | 27 | 900 | 810 | 26,42 | 729 | 0,0215 | ||||||||||||
| 4 | 35 | 27 | 1225 | 945 | 29,33 | 729 | 0,0863 | ||||||||||||
| 5 | 36 | 32 | 1296 | 1152 | 29,92 | 1024 | 0,0650 | ||||||||||||
| 6 | 38 | 31 | 1444 | 1178 | 31,08 | 961 | 0,0026 | ||||||||||||
| 7 | 39 | 33 | 1521 | 1287 | 31,67 | 1089 | 0,0403 | ||||||||||||
| 8 | 41 | 35 | 1681 | 1435 | 32,83 | 1225 | 0,0620 | ||||||||||||
| 9 | 42 | 34 | 1764 | 1428 | 33,42 | 1156 | 0,0171 | ||||||||||||
| 10 | 45 | 32 | 2025 | 1440 | 35,17 | 1024 | 0,0991 | ||||||||||||
| å | 358 | 298 | 13210 | 10898 | 298 | 9042 | 0,4434 | ||||||||||||
| среднее | 35,8 | 29,8 | |||||||||||||||||
| Коэффициенты регрессии: | |||||||||||||||||||
| b | 0,583 | ||||||||||||||||||
| a | 8,917 | ||||||||||||||||||
| Уравнение регрессии: Y= | 8,917+0,583*Х | ||||||||||||||||||
| Коэффициент парной корреляции: | |||||||||||||||||||
| ЧИСЛИТ | 2296 | ||||||||||||||||||
| ЗНАМЕН | 2522 | ||||||||||||||||||
| R | 0,91 | ||||||||||||||||||
| Средняя относительная ошибка прогнозирования: | |||||||||||||||||||
| E= | 4,43439 | ||||||||||||||||||
Диаграмма6
| 25 | 23 | 23,5 |
| 27 | 24 | 24,67 |
| 30 | 27 | 26,42 |
| 35 | 27 | 29,33 |
| 36 | 32 | 29,92 |
| 38 | 31 | 31,08 |
| 39 | 33 | 31,67 |
| 41 | 35 | 32,83 |
| 42 | 34 | 33,42 |
| 45 | 32 | 35,17 |
Похожие работы
-
Обеспечение надежности действующих ТЭС
На каждой ТЭС устанавливается состав работ по техническому обслуживанию с указанием периодичности их выполнения, назначаются персональных ответственные исполнители.
-
Сетевые графики 2
Федеральное агентство по образованию ГОУВПО «Удмуртский государственный университет» Институт экономики и управления Кафедра управления социально-экономическими системами
-
Основные временные параметры сетевых графиков и их расчеты
Теория графов. Параметры сетевого графика. Наиболее ранний из возможных сроков совершения того или иного события. Расчет основных временных параметров. Путь в сетевом графике. Опасность срыва наступления завершающего события. Частный резерв времени.
-
Сетевые методы в планировании
Кафедра прикладной математики Курсовая работа по курсу: “Дискретная математика” по теме: “Сетевые методы в планировании”
-
Решение задач по эконометрике 2
Задача 1 Вариант Провести корреляционно регрессионный анализ в зависимости выплаты труда от производительности труда для этого: 1. Построить поле корреляции и выбрать модель уравнения.
-
СМО с отказами
СМО с отказами (задача Эрланга) Рассматривается N-канальная СМО с отказами: λпотерь λобслуживания υ υ υ λ Любая заявка может быть обслужена любым свободным каналом. Если все каналы заняты, заявка немедленно получает отказ в обслуживании и покидает систему (теряется).
-
Контрольная работа по Экономико-математическим методам и модели в отрасли связи
Министерство Российской Федерации по связи и информатизации Сибирский Государственный Университет Телекоммуникаций и Информатики Межрегиональный центр переподготовки специалистов
-
Сетевое планирование 2
Содержание Введение…………………………………………………………………………5 1. Основные понятия сетевого планирования и управления…………….…..7 1.1 Основные параметры сетевой модели системы планирования и управления………………………………………………………………….7
-
Сетевые методы планирования и управления
Национальный Технический Университет Украины (КПИ) Кафедра АСОИУ КУРСОВАЯ РАБОТА по предмету: "Организация и планирование производства"
-
Уравнения регрессии. Коэффициент эластичности, корреляции, детерминации и F-критерий Фишера
Автономная некоммерческая организация Высшего профессионального образования «ПЕРМСКИЙ ИНСТИТУТ ЭКОНОМИКИ И ФИНАНСОВ» Факультет Экономический