Referat.me / Математика / Интересные примеры в метрических пространствах

Название: Интересные примеры в метрических пространствах

Вид работы: реферат

Размер файла: 23.41 Kb

Скачать файл: referat.me-215501.docx

Краткое описание работы: Интересные примеры в метрических пространствах: 1. В n-мерном евклидовом пространстве полная ограниченность совпадает с обычной ограниченностью, то есть с возможностью заключить данное множество в достаточно большой куб. Действительно, если такой куб разбить на кубики с ребром , то вершины этих кубиков будут образовывать конечную

Интересные примеры в метрических пространствах

Интересные примеры

в метрических пространствах:

1. В n - мерном евклидовом пространстве полная ограниченность совпадает с обычной ограниченностью, то есть с возможностью заключить данное множество в достаточно большой куб. Действительно, если такой куб разбить на кубики с ребром e, то вершины этих кубиков будут образовывать конечную -сеть в исходном кубе, а значит, и подавно, в любом множестве, лежащем внутри этого куба.

1. Единичная сфера S в пространстве l ₂ дает нам пример ограниченного, но не вполне ограниченного множества. Рассмотрим в S точки вида:

е ₁ =(1, 0, 0, ..., 0, 0, ...),

е ₂ =(0, 1, 0, ..., 0, 0, ...),

…………………………,

е _n =(0, 0, 0, ..., 1, 0, ...),

………………………….

Расстояние между любыми двумя точками е _n и е _м (n ¹ m ) равно Ö2. Поэтому последовательность {е _i } и любая ее подпоследовательность не сходятся. Отсюда в S не может быть конечной e-сети ни при каком e<Ö2/2.

2. Рассмотрим в l ₂ множество П точек

x=(x₁ , x₂ , ¼, x_n , ...),

удовлетворяющих условиям:

| x₁ |£1, | x₂ |£1/2, ¼,| x_n |£1/2ⁿ ^-1 , ...

Это множество называется фундаментальным параллепипедом («гильбертовым кирпичем») пространства l ₂ . Оно представляет собой пример бесконечномерного вполне ограниченного множества. Для доказательства его полной ограниченности поступим следующим образом.

Пусть e>0 задано. Выберем n так, что 1/2^n-1 <e/2. Каждой точке x=(x₁ , x₂ , ¼, x_n , ...)

из П сопоставим точку x*=(x₁ , x₂ , ¼, x_n , 0, 0, ...)

из того же множества. При этом

r(x,x*)=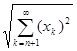£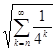<1/2ⁿ ^-1 <e/2.

Множество П* точек вида x*=(x₁ , x₂ , ¼, x_n , 0, 0, ...) из П вполне ограничено (как ограниченное множество в n -мерном пространстве). Выберем в П* конечную e/2-сеть. Она будет в то же время e-сетью во всем П . Докажем это.

Доказательство : для "e>0, выберем n так, что 1/2ⁿ ^-1 <e/2.

"xÎП : x=(x₁ , x₂ , ¼, x_n , ...) сопоставим

x*=(x₁ , x₂ , ¼, x_n , 0, 0, ...) и x*ÎП . При этом r(x,x*)<e/2. Из пространства П выберем x**: r(x*,x**)<e/2.

Тогда: r(x,x**)£r(x,x*)+r(x*,x**)<e/2+e/2=e.

Множество П* содержит точки вида x*=(x₁ , x₂ , ¼, x_n , 0, 0, ...), в этом множестве выберем конечную e/2-сеть. Она будет e-сетью в пространстве П , так какr(x,x**)<e.

Интересные примеры в метрических пространствах

Пусть e>0 задано. Выберем n так, что 1/2n-1 <e/2. Каждой точке x=(x1 , x2 , ¼, xn , ...)

Похожие работы

Пусть e>0 задано. Выберем n так, что 1/2^n-1 <e/2. Каждой точке x=(x₁ , x₂ , ¼, x_n , ...)