Методы предварительных эквивалентных преобразований и итерационные методы с минимизацией невязки для решения СЛАУ

Реферат « Введение в численные методы »

Тема: «Методы предварительных эквивалентных преобразований и итерационные методы с минимизацией невязки для решения СЛАУ»

1. Методы предварительных эквивалентных преобразований

1.1 Преобразование вращения

Следующий важный подход к решению алгебраических систем уравнений базируется на применении эквивалентных преобразований с помощью унитарных матриц, сводящем исходную матрицу к эквивалентной ей диагональной.

Смысл этого подхода состоит в том, чтобы последовательно, умножением слева и / или справа на специальные унитарные матрицы, превратить некоторые компоненты исходной матрицы в нуль.

Матрица S называется унитарной, если ее произведение со своей комплексно сопряженной равно единичной матрице. Это означает, что комплексно сопряженная матрица равна обратной матрице:

Известной унитарной матрицей является матрица вращения ,которая применяется для поворота на заданный угол вектора, принадлежащего некоторой плоскости, вокруг начала координат. В двумерном случае вектор поворачивается на угол путем умножения на матрицу

Чтобы сохранить эквивалентность результирующей матрицы при умножении ее на матрицу вращения, необходимо исходную матрицу умножать справа на и слева на . Умножение же матрицы вращения на вектор дает такой же по величине вектор, но повернутый на заданный угол.

Поворот вектора в многомерном пространстве на произвольный угол можно представить, как последовательность плоских вращений каждой проекции на некоторый угол. Если подобрать угол вращения так, чтобы в плоском повороте одну из проекций вектора совместить с координатной осью, то вторая проекция в этой плоскости становится равной нулю.

Частные повороты вектора в многомерном пространстве с помощью матрицы вращения можно выполнять, если ее расширить до матрицы размера следующим образом:

.

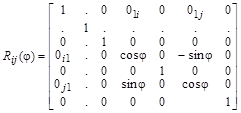Индексы i, j обозначают матрицу вращения, поворачивающую вектор в плоскости на угол .

Теперь частное эквивалентное преобразование матрицы A вращением на угол записываются так:

.

Условие превращения в нуль ij- тых элементов симметричной матрицы A можно получить методом неопределенных коэффициентов на двумерной матрице:

.

.

Угол поворота, при котором , находится из уравнения

.

Разделив на и обозначив , , получим квадратное уравнение для тангенса требуемого угла поворота

.

Из двух решений для тангенса выбирается такое, чтобы . В этом случае . Подставив выражение для угла в соотношения для диагональных элементов, после тригонометрических преобразований получаются следующие формулы:

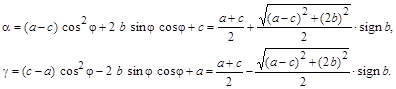
Для получения результирующей матрицы выполнять матричное умножение трех матриц совсем необязательно. Структура матриц вращения вызывает при умножениях изменение только тех элементов исходной матрицы, которые находятся на i- той и j- той строчках и на i- том и j- том столбцах. Изменения представляются суммами элементов, стоящих в строчках и столбцах, умноженных на синус или косинус угла в соответствии с формулами, где j>i :

преобразования строк – ;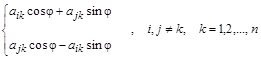

преобразование столбцов –.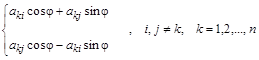

На пересечениях i -й строки и i- того столбца и j -й строки и j- того столбца располагаются соответственно вычисленные выше и , а на местах ij -того и ji -того элементов вставляются нули.

Для приведения к диагональной матрице необходимо выполнить таких элементарных преобразований.

1.2 Ортогональные преобразования отражением

Следующей важной унитарной матрицей, с помощью которой в различных алгоритмах выполняются ортогональные преобразования, являются матрицы отражения. Использование этого инструмента позволяет, например, последовательными эквивалентными преобразова-ниями свести исходную матрицу к верхней треугольной (QR-алгоритмы), трех или двух диагональным и т.д.

Смысл этого подхода состоит в том, чтобы умножением матрицы A слева на специально подобранную унитарную матрицу один из столбцов исходной матрицы (например, ) преобразовать в вектор, параллельный единичному координатному вектору (или ). Тогда, последовательно подбирая нужные унитарные матрицы и соответствующие единичные векторы , после n циклов эквивалентных преобразований можно будет получить верхнюю треугольную матрицу:

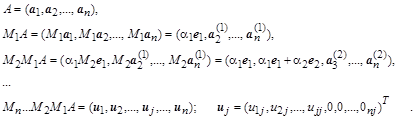
При выборе в качестве начального вектора и умножениях матрицы A на ортогональные матрицы справа в конечном счете можно получить нижнюю треугольную матрицу.

Весь вопрос состоит в том, как формировать унитарную матрицу с заданными свойствами из векторов и столбцов матрицы A .

Из аналитической геометрии известно, что любые векторы, лежащие в плоскости, взаимно перпендикулярны с ее нормалью, т.е. их проекции на нормаль равны нулю. Последнее эквивалентно равенству нулю скалярных произведений.

Чтобы (k+ 1) – мерный векторный треугольник сделать параллельным k- мерной гиперплоскости с нормалью n (вектор единичной длины, перпендикулярный плоскости), необходимо приравнять нулю скалярное произведение: (n , y )=0.

Пусть вектор z не параллелен плоскости, заданной своей нормалью, тогда его проекции на эту плоскость и нормаль соответственно будут представлены векторами и . Вектор z и вектор зеркально-симметричный ему через эти проекции можно выразить так:

Разрешив первое относительно и подставив его в , получим

Проекцию вектора можно заменить скалярным произведением (n , z ) и подставить в выражение для , выразив тем самым зеркально отраженный вектор через исходный вектор и нормаль гиперплоскости:

Здесь M представляет унитарную матрицу, преобразующую произвольный вектор в зеркально отраженный. В том, что матрица унитарная, нетрудно убедиться, проверив ее произведение со своей комплексно сопряженной:

Выражение для зеркально отраженного вектора позволяет представить нормальный вектор в виде линейной функции от задаваемого вектора z :

Число в знаменателе является нормирующим множителем. Нормальный вектор представляющий гиперплоскость обязан иметь единичную длину. Коэффициент , который в общем случае является комплексным числом, необходимо выбрать так, чтобы скалярное произведение было больше нуля. Если учесть соотношение для согласованных норм: , то

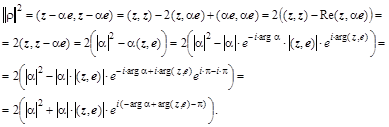
Выбрав для комплексных матриц или – для действительных матриц, будем иметь

Такое нормирование не нарушает коллинеарности отраженного и единичного векторов:

Рассмотрим пример воздействия ортогонального преобразования на матрицу

.

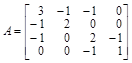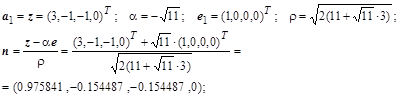
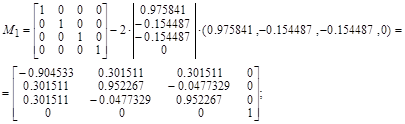
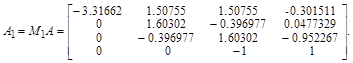
Приведенная методика получения унитарных (и ортогональных в частности) матриц используется во многих стандартных алгоритмах в качестве инструмента частичного преобразования исходных матриц к двух или трех диагональным, для которых в дальнейшем применяются рекуррентные формулы получения решения уравнений, называемые в литературе методом прогонки для систем с ленточными матрицами.

2. Итерационные методы с минимизацией невязки

2. 1 Ускорение сходимости итерационных методов

Точные методы получения решений, использующие рассмотренные эквивалентные преобразования полностью заполненной матрицы, требуют выполнения числа операций, пропорционального кубу размерности системы, и свободной памяти для хранения исходных и промежуточных значений – пропорциональной квадрату размера матрицы. Поэтому для сверх больших систем (число неизвестных больше нескольких сотен) ориентируются в основном на применение приближенных, итерационных методов.

Привлекательность тех или иных итерационных методов определяется скоростью сходимости итерационного процесса. Теоретически доказано, что итерационный процесс Гаусса-Зейделя сходится к решению при любом начальном значении искомого значения вектора решений, однако количество итерационных циклов может во много раз превышать число неизвестных (размерность матрицы). Это вызвало к жизни множество модификаций алгоритмов, обладающих большей скоростью сходимости.

Процедуры ускорения связаны с построением очередного вектора по одному или нескольким его значениям на предыдущих итерационных циклах. Фактически речь идет о построении на каждом шаге итераций интерполирующей функции с векторным аргументом, по которой вычисляют очередной вектор для подстановки. Для вычисления вектора на (k+ 1) – ом шаге итераций необходимо сначала получить величину и единичный вектор направления и просуммировать предыдущий вектор с добавочным вектором:

.

Подстановка последнего в уравнение () образует вектор из покомпонентных невязок. Для задания структурной взаимосвязи каждой невязки с соответствующей компонентой вектора и образования функционала (скалярной функции от вектора невязок) возмем скалярное произведение вектора невязки на вектор-строку :

.

После подстановки очередного вектора функционал получит новое значение, которое будет зависеть от некоторого скаляра :

.

Чтобы невязки на каждом шаге итераций становились меньше, желательно соответствующим образом выбирать . Найдем такое значение , при котором . Для этого приравняем производную по нулю. Индекс номера итерации пока опустим.

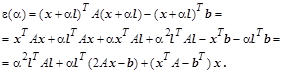
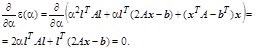
Из последнего равенства для (k+ 1) – й итерации величина шага в направлении вектора должна быть вычислена так:

.

Если единичные векторы направления последовательно выбирать равными координатным, т.е. , то будет реализован метод Гаусса-Зейделя (метод покоординатного спуска в задачах оптимизации).

Выбирая направление изменения очередного вектора в сторону локального убывания, т.е. в сторону, противоположную вектору градиента функционала, получается метод быстрого спуска. В этом случае

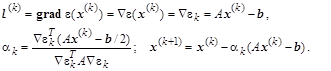
2.2 Метод сопряженных направлений

Среди методов, связанных с выбором направления существуют методы, в которых к векторам направлений предъявляются требования их взаимной сопряженности , т.е. матрица A преобразует вектор в вектор, ортогональный вектору . Доказано, что выбор направлений из множества сопряженных позволяет при любом начальном свести задачу к точному решению не более, чем за n шагов, если матрица симметричная и положительно определенная () размера .

Классическим набором сопряженных векторов являются собственные векторы матрицы (). Однако задача их определения сложнее решения заданной системы уравнений. Не менее сложна и задача построения произвольной системы ортогональных векторов.

В то же время примером ортогональных направлений являются направления вектора градиента и нормали в заданной точке некоторой гиперповерхности. Такая поверхность выше была представлена функционалом в виде скалярного произведения вектора невязки и вектора x , которая и определяла направление спуска по направлению градиента. Если, используя такой же подход к вычислению , в выражении для последнего вектор невязок дополнительно модифицировать, как показано ниже, то рекуррентно вычисляемые очередные направления окажутся сопряженными:

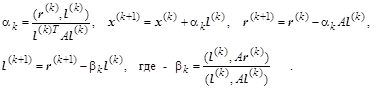
Выбрав в начале итераций и , после выполнения приведенных вычислений в (n- 1) цикле будут получены векторы направлений, удовлетворяющие соотношениям

,

а векторы невязок будут ортогональными:

.

Относительно метода сопряженных градиентов доказывается, что, если матрица (положительно определенная и симметричная) имеет только m (m<n ) различных собственных значений, то итерационный процесс сходится не более, чем за m итераций. Однако в практической реализации скорость сходимости существенно зависит от величины меры обусловленности и в итерационном процессе может быть оценена согласно неравенству:

,

где – коэффициент, степень которого на каждом шаге итерационного процесса показывает во сколько раз уменьшилось расстояние до вектора точного решения x *.

Чем больше , тем ближе a к единице и, следовательно, степени a уменьшаются медленнее. В литературе описываются модифицированные методы сопряженных градиентов, которые тем или иным способом включают в итерационный процесс подобные (конгруэнтные – для комплексных матриц) преобразования, предварительно уменьшающие меру обусловленности.

Литература

1. Бахвалов И.В. Численные методы. БИНОМ, 2008. – 636c.

2. Волков Е.А. Численные методы. Изд-во ЛАНЬ, 2004. – 256.

3. Демидович Б.П., ред., Марон И.А., Шувалова Э.З. Численные методы анализа. Издательство ЛАНЬ, 2008.

4. Пантелеев А.В., Киреев В.И., Пантелеев В.И., Киреев А.В. Численные методы в примерах и задачах. М: Высшая школа, 2004. – 480c.

5. Пирумов У.Г., Пирумов О.Г. Численные методы. Изд-во: ДРОФА, 2004. – 224c.