Название: Методы преобразования комплексного чертежа
Вид работы: реферат
Рубрика: Математика
Размер файла: 65.04 Kb
Скачать файл: referat.me-215742.docx
Краткое описание работы: Четыре основные задачи, решаемые методами преобразования. Сущность способа замены плоскостей проекций. Решение ряда задач по преобразованию прямой общего положения в прямую уровня, а затем - в проецирующую, выполнив последовательно два преобразования.
Методы преобразования комплексного чертежа
План
1. Общие сведения.
2. Замена плоскостей проекций.
3. Вращение вокруг оси, перпендикулярной плоскости проекций.
4. Плоскопараллельное движение.
1. Общие сведения
Проецируемая фигура может занимать по отношению к плоскости проекции удобное (рациональное) и неудобное (нерациональное) положение.
Количество и характер геометрических построений при графическом решении задач определяется не только сложностью самой задачи, но и зависят от рационального или нерационального расположения фигуры относительно плоскости проекций.
Наиболее рациональные частные положения фигуры:
- положение, перпендикулярное к плоскости проекций;
- положение параллельное плоскости проекций.
При общем положении фигуры, она проецируется на плоскость проекций в искаженном виде.
Методы преобразования комплексного чертежа применяются для приведения фигуры общего положения в частное положение, наиболее выгодное для решения задач.
Четыре основные задачи, решаемые методами преобразования
1. Прямую общего положения преобразовать в прямую уровня.
2. Прямую общего положения преобразовать в проецирующую прямую.
3. Плоскость общего положения преобразовать в проецирующую плоскость.
4. Плоскость общего положения преобразовать в плоскость уровня.
Достигается это:
а) введением дополнительных плоскостей проекций так, чтобы прямая линия или плоская фигура, не меняя своего положения в пространстве, оказалась в частном положении в новой системе плоскостей проекций (способ перемены плоскостей проекций);
б) изменением положения прямой линии или какой-либо фигуры путем поворота вокруг некоторой оси так, чтобы прямая или фигура оказалась в частном положении относительно неизменной системы плоскостей проекций (способ вращения и плоскопараллельного перемещения).
2. Замена плоскостей проекций
Сущность способа замены плоскостей проекций заключается в том, что при неизменном положении объекта в пространстве производится замена данной системы плоскостей проекций новой системой взаимно перпендикулярных плоскостей проекций (рис. 75).
При переходе к новой системе одну из плоскостей проекций заменяют новой таким образом, чтобы данный геометрический элемент (прямая, плоскость) занял частное положение и проецировался без искажения.
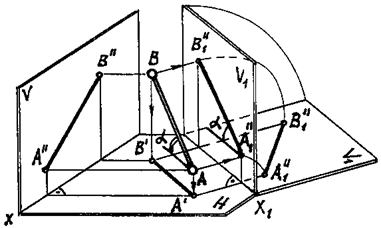
Рис. 75
При решении ряда задач, например, требуется преобразовать прямую общего положения в прямую уровня, а затем — в проецирующую, выполнив при этом последовательно два преобразования.
Рассмотрим ход решения задач.
РЕШЕНИЕ I ОСНОВНОЙ ЗАДАЧИ. Для того, чтобы прямая АВ стала линией уровня (рис. 76, а), следует ввести новую плоскость проекций и расположить ее параллельно данной прямой. При этом новая ось x 1 будет параллельна одной из проекций прямой. Проведем ось параллельно горизонтальной проекции АВ . Новая плоскость проекций V1 расположится параллельно прямой АВ , которая проецируется на эту плоскость в истинную величину* .
Правило: при замене плоскостей проекций расстояние от новой проекции точки до новой оси равно расстоянию от заменяемой проекции точки до старой оси проекций.
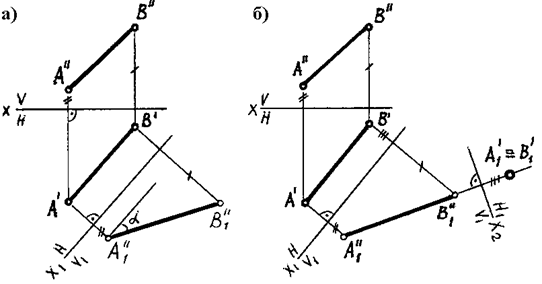
Рис. 76
|
|
Иными словами, высоты (аппликаты) концов отрезка в новой системе плоскостей проекций останутся прежними. В результате этой замены решена задача на определение действительной величины отрезка и угла наклона к плоскости H. На чертеже плоскость V1 совмещают с плоскостью H.
РЕШЕНИЕ II ОСНОВНОЙ ЗАДАЧИ. Для того, чтобы прямая АВ оказалась проецирующей (рис. 76,б), т.е. изобразилась точкой, необходимо решить I основную задачу, а затем произвести вторую замену плоскости проекций и расположить новую плоскость H1 перпендикулярно прямой. Новую ось x 2 располагаем перпендикулярно новой фронтальной проекции прямой А ²1 В ²1 . На новой плоскости проекций Н1 прямая изобразится точкой, так как координаты концов отрезка в системе Н/V1 одинаковы.
Таким образом, прямая АВ в системе H1 /V1 стала проецирующей относительно плоскости H1 . Преобразования в этой задаче могли быть выполнены и в другой последовательности: сначала могла быть заменена горизонтальная плоскость проекций, а затем — фронтальная.
Рассмотрим еще одну задачу — требуется определить истинную величину плоской фигуры — треугольника АВС , занимающего в пространстве общее положение. Для решения этой задачи необходимо преобразовать чертеж (эпюр) так, чтобы плоскость общего положения стала параллельной одной из плоскостей проекций новой системы* .
РЕШЕНИЕ III ОСНОВНОЙ ЗАДАЧИ. Сначала заменим фронтальную плоскость проекций новой плоскостью V1 , перпендикулярной плоскости треугольника. Это условие выполнено с помощью вспомогательной прямой — линии уровня (горизонталь AN ) (рис. 77). Новая ось x 1 проводится перпендикулярно горизонтальной проекции горизонтали. На новой плоскости проекций V1 горизонталь спроецировалась в точку, а плоскость треугольника — в линию. Угол определяет угол наклона треугольника к горизонтальной плоскости H.
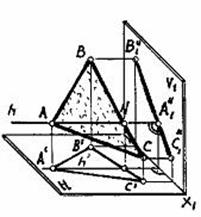
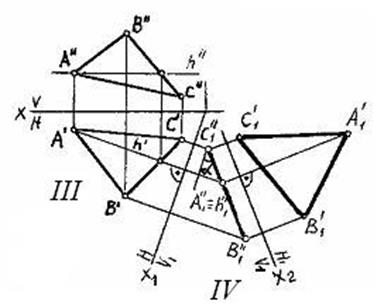
Рис. 77
|
|
РЕШЕНИЕ IV ОСНОВНОЙ ЗАДАЧИ. Для решения задачи новая плоскость проекций должна быть параллельна заданной плоскости. Производим две последовательные перемены. При первой перемене располагаем новую плоскость проекций перпендикулярно к прямой уровня заданной плоскости общего положения, т.е. решаем третью основную задачу – преобразуем плоскость общего положения в проецирующую. При второй перемене новую плоскость проекций H1 устанавливаем параллельно треугольнику. Новую ось x 2 проводим параллельно новой фронтальной проекции треугольника — прямой B ²1 A ²1 C ²1 . Построенная проекция определяет истинную величину и форму треугольника.
* Новая ось x 1 и плоскость проекции V1 могут быть расположены на любом расстоянии от прямой, они могут совпадать с прямой и ее проекцией
* Сначала следует преобразовать плоскость общего положения в проецирующую, а затем — в плоскость уровня.
Похожие работы
-
Методы проецирования
Для отображения точек оригинала на чертеже применяют операцию проецирования. Имеется плоскость проецирования (ее иногда называют картинная плоскость), на которой получается изображение оригинала - точки А. Операция проецирования заключается в проведении через точку А прямой, которая называется проецирующей.
-
Место прямой в начертательной геометрии
Понятие начертательной геометрии, ее сущность и особенности, предмет и методы изучения, история зарождения и развития. Цели и задачи начертательной геометрии, ее структура и элементы. Прямая и варианты ее расположения, разновидности и методы определения
-
Построение теней
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ КАЗАХСТАН МЕЖДУНАРОДНАЯ ОБРАЗОВАТЕЛЬНАЯ КОРПОРАЦИЯ КАЗАХСКАЯ ГОЛОВНАЯ АРХИТЕКТУРНО-СТРОИТЕЛЬНА АКАДЕМИЯ
-
Прямое дискретное преобразование Лапласа
Предмет: Теория Автоматического Управления Тема: ПРЯМОЕ ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ЛАПЛАСА Введение Динамические процессы в дискретных системах управления описываются уравнениями в конечных разностях. Удобным методом для решения разностных уравнений является операционный метод, основанный на дискретном преобразовании Лапласа.
-
Решение задач на построение сечений многогранников
Содержание: Из истории начертательной геометрии Виды проецирования Пересечение многогранников плоскостью (описание метода) Примеры задач Список используемой литературы
-
Проекция геометрических объектов
Особенности использования метода секущих плоскостей для создания проекции и разветки пересечения поверхностей фигур. Порядок построения изометрии взаимного пересечения поверхностей фигур. Характеристика процесса создания фигуры с вырезом, опоры и стойки.
-
Неединственность преобразований Лоренца.
Основа физики – геометрия. Она определяет способы задания координат. Преобразования их единственны и это преобразования Лоренца внутри изотропного конуса. На поверхности изотропного конуса эти преобразования не обладают единственностью. Расстояние света.
-
Плоскости и их проекции
Понятие плоскости и определение ее положения в пространстве. Задание плоскости ее следами на комплексном чертеже. Плоскости и проекции уровня. Свойство проецирующих плоскостей собирать одноименные проекции всех элементов, расположенных в данной плоскости.
-
Перпендикулярность геометрических элементов
Теорема о проецировании прямого угла, возможные три случая такого проецирования. Главные линии плоскости: линии уровня и линии наибольшего наклона. Прямая, перпендикулярная к плоскости и ее проекции. Условие взаимной перпендикулярности двух плоскостей.
-
Аффинные преобразования на плоскости
ПГУ им. Т.Г.Шевченко Курсовая работа. Тема: Аффинные преобразования на плоскости. Выполнила студентка 110 гр. физико-математического ф-та Пельтек Е.С.
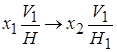 ;
;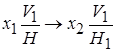 ;
;