Название: Плоскости и их проекции
Вид работы: реферат
Рубрика: Математика
Размер файла: 38.51 Kb
Скачать файл: referat.me-215757.docx
Краткое описание работы: Понятие плоскости и определение ее положения в пространстве. Задание плоскости ее следами на комплексном чертеже. Плоскости и проекции уровня. Свойство проецирующих плоскостей собирать одноименные проекции всех элементов, расположенных в данной плоскости.
Плоскости и их проекции
План
1. Проекции плоскостей общего положения
2. Проекции плоскостей уровня
Горизонтальная плоскость
Фронтальная плоскость
Профильная плоскость
3. Проекции проецирующих плоскостей
Горизонтально-проецирующая плоскость
Фронтально-проецирующая плоскость
Профильно-проецирующая плоскость
4. Взаимное расположение двух плоскостей
Параллельные плоскости
Пересекающиеся плоскости
5. Пересечение плоскостей общего положения
6. Взаиморасположение прямой и плоскости
Прямая - в плоскости
Прямая, параллельная плоскости
Прямая пересекает плоскость
7. Пересечение прямой с плоскостью
8. Условие видимости на чертеже
1. Проекции плоскостей общего положения
На комплексном чертеже плоскость может быть задана изображениями тех геометрических элементов, которые вполне определяют положение плоскости в пространстве. Это:
1) три точки, не лежащие на одной прямой (рис. 30);
2) прямая и точка вне прямой;
3) две параллельные прямые (рис. 27);
4) две пересекающиеся прямые (рис. 28).
При решении некоторых задач целесообразно задавать на комплексном чертеже плоскость ее следами (рис. 31).
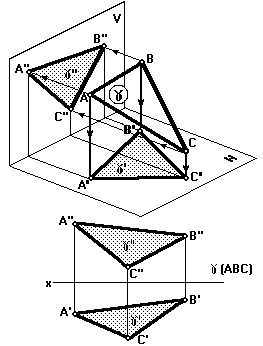 |
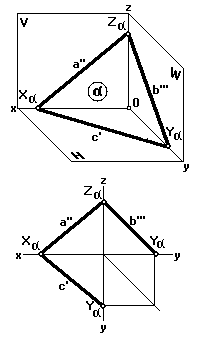 |
| Рис. 30 | Рис. 31 |
СЛЕДОМ ПЛОСКОСТИ называется прямая, по которой данная плоскость пересекается с плоскостью проекций.
На рис. 31 изображена плоскость и ее следы: с — горизонтальный; а — фронтальный; b — профильный. Следы плоскости сливаются с одноименными своими проекциями: след с = с'; след а = а''; след b = b'''. Точки ![]() называются точками схода следов.
называются точками схода следов.
2. Проекции плоскостей уровня
Плоскостями уровня называются плоскости, параллельные плоскостям проекций.
Характерная особенность этих плоскостей состоит в том, что элементы, расположенные в этих плоскостях, проецируются на соответствующую плоскость проекций в натуральную величину.
Горизонтальная плоскость
Горизонтальная плоскость (рис. 32) параллельна горизонтальной плоскости проекций.
На двухкартинном комплексном чертеже она изображается одним фронтальным следом, параллельным оси x.
На рис. 32 изображена горизонтальная плоскость (V ).
Фронтальная плоскость
Фронтальная плоскость (рис. 33) параллельна фронтальной плоскости проекций.
На двухкартинном комплексном чертеже она изображается одним фронтальным следом, параллельным оси x.
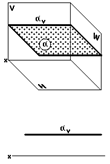
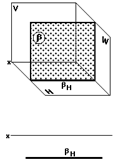
| Рис. 32 | Рис. 33 |
На рис. 33 изображена фронтальная плоскость ( ).
Профильная плоскость
Профильная плоскость (рис. 34) параллельна профильной плоскости проекций.
На двухкартинном комплексном чертеже она изображается двумя следами: горизонтальным и фронтальным, перпендикулярными оси x.
На рис. 34 изображена профильная плоскость (H,V ).
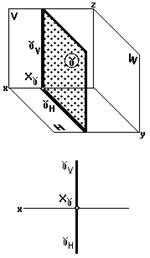
Рис. 34
3. Проекции проецирующих плоскостей
ПРОЕЦИРУЮЩИМИ называются плоскости, перпендикулярные к плоскостям проекций.
Характерной особенностью таких плоскостей является их собирательное свойство. Оно заключается в следующем: соответствующий след — проекция плоскости — собирает одноименные проекции всех элементов, расположенных в данной плоскости.
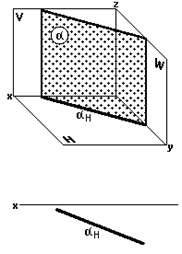
Горизонтально-проецирующая плоскость
Горизонтально-проецирующая плоскость (рис. 33) перпендикулярна к горизонтальной плоскости проекций H.
 |
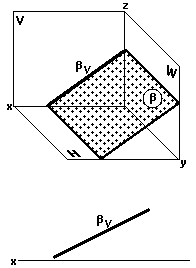 |
| Рис. 35 | Рис. 36 |
Горизонтальные проекции всех точек, принадлежащих горизонтально-проецирующей плоскости , располагаются на горизонтальном следе — проекции H этой плоскости (рис. 35).
Фронтально-проецирующая плоскость
Фронтально-проецирующая плоскость (рис. 36) перпендикулярна к фронтальной плоскости проекций V.
Фронтальные проекции всех точек, принадлежащих фронтально-проецирующей плоскости , располагаются на фронтальном следе — проекции этой плоскости (рис. 36).
Профильно-проецирующая плоскость
Профильно-проецирующая плоскость (рис. 37) перпендикулярна к профильной плоскости проекций W.
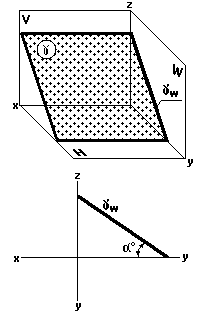
Рис. 37
Профильные проекции всех точек, принадлежащих профильно-проецирующей плоскости , располагаются на профильном следе —проекции этой W плоскости (рис. 37).
Похожие работы
-
Методы проецирования
Для отображения точек оригинала на чертеже применяют операцию проецирования. Имеется плоскость проецирования (ее иногда называют картинная плоскость), на которой получается изображение оригинала - точки А. Операция проецирования заключается в проведении через точку А прямой, которая называется проецирующей.
-
Место прямой в начертательной геометрии
Понятие начертательной геометрии, ее сущность и особенности, предмет и методы изучения, история зарождения и развития. Цели и задачи начертательной геометрии, ее структура и элементы. Прямая и варианты ее расположения, разновидности и методы определения
-
Построение теней
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ КАЗАХСТАН МЕЖДУНАРОДНАЯ ОБРАЗОВАТЕЛЬНАЯ КОРПОРАЦИЯ КАЗАХСКАЯ ГОЛОВНАЯ АРХИТЕКТУРНО-СТРОИТЕЛЬНА АКАДЕМИЯ
-
Контрольная работа по Начертательной геометрии
Контрольная работа Задание № 1. Для фермы, изображённой на схеме: Посчитать степень статической определимости. Сделать проверку на мгновенную и геометрическую неизменяемости.
-
Проводники в электрическом поле. Электростатический метод изображений
Проводники в электрическом поле. Электростатический метод изображений. М.И. Векслер, Г.Г. Зегря Поле внутри проводника равно нулю, поэтому проводники геометрически ограничивают область, где должны решаться уравнения электростатики. На поверхности проводника φ = const (эквипотенциальность).
-
Билеты по геометрии
Параллельность прямых, параллельность прямой и плоскости, перпендикулярность прямых и плоскостей, формула объема конуса.
-
Декартовыми прямоугольными координатами
Декартовыми прямоугольными координатами точки P на плоскости в двухмерной системе координат называются взятые с определенным знаком расстояния (выраженные в единицах масштаба) этой точки до двух взаимно перпендикулярных прямых — осей координат или проекции радиус-вектора r точки P на две взаимно перпендикулярные координатные оси.
-
Метод вспомогательных секущих сфер
Уфимский государственный авиационный технический университет Кафедра начертательной геометрии и черчения МЕТОД ВСПОМОГАТЕЛЬНЫХ СЕКУЩИХ СФЕР (концентрических и эксцентрических)
-
Перпендикулярность геометрических элементов
Теорема о проецировании прямого угла, возможные три случая такого проецирования. Главные линии плоскости: линии уровня и линии наибольшего наклона. Прямая, перпендикулярная к плоскости и ее проекции. Условие взаимной перпендикулярности двух плоскостей.
-
Методы преобразования комплексного чертежа
Четыре основные задачи, решаемые методами преобразования. Сущность способа замены плоскостей проекций. Решение ряда задач по преобразованию прямой общего положения в прямую уровня, а затем - в проецирующую, выполнив последовательно два преобразования.