Название: Побудова зображень предметів на площині

Вид работы: реферат

Рубрика: Математика

Размер файла: 1.6 Mb

Скачать файл: referat.me-215758.docx

Краткое описание работы: Сутність методу проекціювання. Центральні та паралельні проекції. Переваги ортогонального проекціювання перед центральним та косокутним. Положення геометричної фігури в просторі і виявлення її форми по ортогональних проекціях. Закони побудови зображень.

Побудова зображень предметів на площині

Житомирський Військовий Інститут

Національного Авіаційного Уніврситету

Реферат

на тему:

Побудова зображень предметів на площині

Житомир 2010

Нарисна геометрія – наука, яка вивчає просторові форми та способи зображення їх на площині.

Основною задачею нарисної геометрії є вивчення методів побудови зображень просторових форм та в розробці способів рішення просторових задач за допомогою зображень.

Предмет, якій зображують називають оригіналом або моделлю. Креслення повинно містити геометричну інформацію про форму та розміри оригіналу. До такого креслення висуваються слідуючи основні вимоги:

– наочність, тобто давати просторове уявлення про модель;

– простота з точки зору графічного виконання;

– точність – графічні операції, які виконуються на кресленні, повинні давати точні рішення.

Для побудови зображень предметів на площині користуються методом проекціювання. Тому наступне питання - метод проекцій.

1. Сутність методу проекціювання

Отже, проекція - це зображення предмета, "відкинуте" на площину за допомогою променів. Спроекціювати предмет — це означає зобразити його на площині (рис.1).

Залежно від положення проекціюючих променівпроекції поділяють на центральні та паралельні.

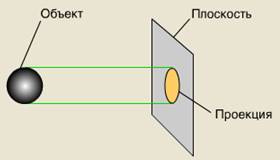
Рис. 1

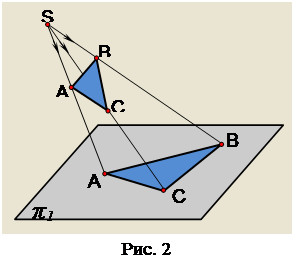
Ідею центрального проекціювання видно з рис.2. Точка S, з якої виходять проекціюючі промені, називається центром проекціювання. Площина π₁ на яку проекціюється предмет, називається площиною проекцій. Площина π₁ і точка S становлять апарат центральної проекції. Щоб спроекціювати трикутник, треба з центра проекцій Sчерез усі його вершини провести проекціюючі промені до перетину з площиною проекцій π_1. Одержимо точки А₁ В₁ С₁ , які називаються центральними проекціями вершин А, В, С на площину π₁ , а трикутник А₁ В₁ С₁ - центральною проекцією трикутника ABC.

Метод паралельного проекціювання розглянемо за допомогою рис. 3. Як і в попередньому випадку, вибирають площину проекцій π₁ . Замість центра проекцій Sзадають напрям проекціювання s, тобто вважають, що центр проекцій Sвіддалений у нескінченність. Тому проекціюючі промені паралельні між собою. Площина π₁ і напрям sстановлять апарат паралельної проекції. Щоб спроекціювати трикутник ABCна площину π₁ , через вершини А, В, С проводять проекціюючі промені паралельно напряму проекціювання s. Внаслідок перетину цих променів з площиною π₁ утворюється трикутник А₁ В₁ С₁ , який являє собою паралельну проекцію трикутника ABC.

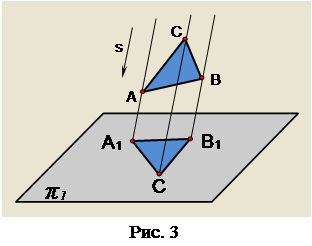
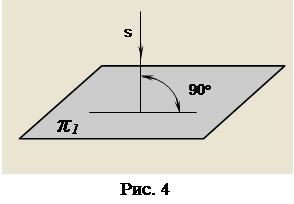
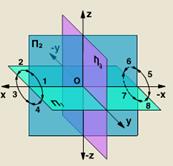
Рис. 5

Паралельні проекції поділяють на прямокутні і косокутні. Якщо проекціюючі промені перпендикулярні до площини проекцій (рис. 4), то таке проекціювання називають прямокутним, а проекції, які при цьому одержують — прямокутними, або ортогональними. Якщо ж кут нахилу променів не дорівнює 90°, то такі паралельні проекції називаються косокутними. У кресленні користуються прямокутними проекціями.

Ортогональне проекціювання має ряд переваг перед центральним та косокутним паралельним проекціюванням:

– простоту геометричних побудов ортогональних проекцій предметів;

– зберігання на проекціях, при певних умовах, форми та величини лінійних та кутових розмірів проекціюючих предметів.

2. Побудова за заданими координатами епюрів прямих, взаємного положення прямих та прямих і точок.

Розглянемо просторову модель координатної площини проекцій. Для визначення положення геометричної фігури в просторі і виявлення її форми по ортогональних проекціях найбільш зручною є декартова система координат. Декартова система координат складається з трьох взаємно перпендикулярних площин.

π₁ – горизонтальна площина проекцій;

π₂ – фронтальна площина проекцій;

π₃ – профільна площина проекцій.

Лінії перетину площин проекцій утворюють осі координат: X - вісь абсцис, Y - вісь ординат, Z - вісь аплікат, а точка перетину координатних осей O береться за початок координат.

π₁ – горизонтальна площина проекцій; π₂ – фронтальна площина проекцій;

Площини проекцій перетинаються по вісі координат Ох . Обертанням навколо вісі Ох площину π₁ суміщають з площиною π₂ . Отримаємо комплексне креслення

Схему побудови зворотного ортогонального креслення розвинув Гаспар Монж – знаменитий французький учений. По схемі Монжа оригінал (наприклад точка) проекціюється ортогонально на дві взаємно перпендикулярні площини проекції π₁ - горизонтальну і π₂ - фронтальну площини проекцій.

Лінія зв'язку - це пряма, що з’єднує дві проекції точки на комплексному кресленні і перпендикулярна осі проекцій.

У результаті ми отримали двохпроекційне комплексне креслення точки А.

Твердження: Дві прямокутні проекції точки повністю визначають її положення в просторі основних площин проекцій.

Тобто комплексне креслення або епюр Монжа (з фр. «креслення») – це зображення, яке отримуємо в результаті обертання площини проекцій π₁ на кут 90° до суміщення π₂ .

В кресленні ж при побудові зображень часто користуються трьома проекціями на три площини проекцій. Розглянемо, за якими законами це реалізується.

Просторова картина			Комплексне креслення

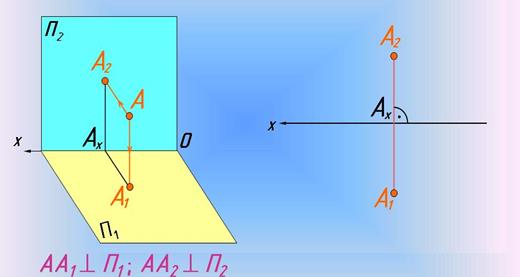
А ₁ – горизонтальна та А ₂ – фронтальна проекції точки А . Проекціюючі промені А А ₁ та А А ₂ перпендикулярні відповідним площинам проекцій. Точки перетину проекціюючої площини з віссю Ох позначена А_Х . На комплексному кресленні горизонтальна А ₁ та фронтальна А ₂ проекції точки А з’єднуються вертикальною лінією проекційного зв’язку, яка ^ вісі Ох .

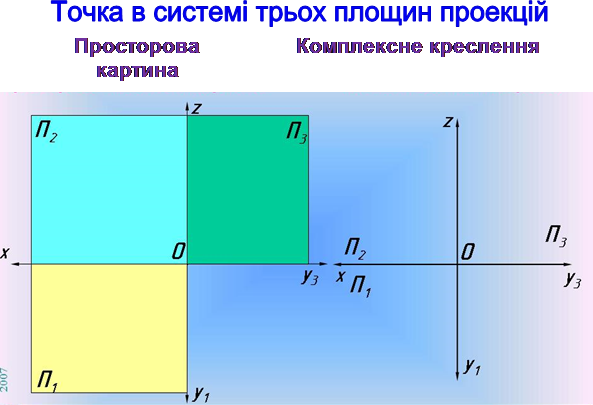
Для переходу до комплексного креслення просторову модель розрізають по вісі Оу та суміщають всі три площини проекцій в одну: π₁ обертають навколо вісі Ох , π₃ обертають навколо вісі О z до їх спів падання з π₂ .Вісь Оу розпадається на дві вісі у ₁ та у ₃

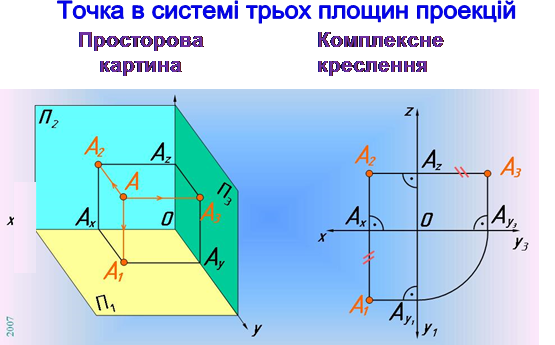
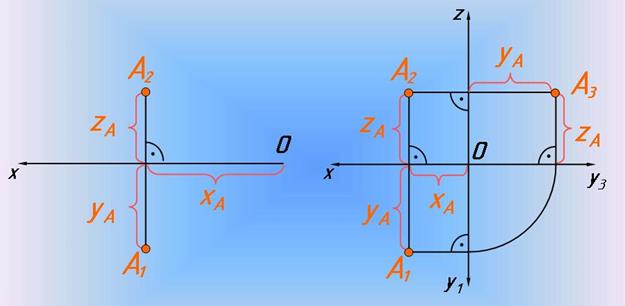
Проекціюючі промені АА ₁ , АА ₂ та АА ₃ проводять перпендикулярно відповідним площинам проекцій й отримують проекції точки А : горизонтальну А ₁ , фронтальну А ₂ та профільну А ₃ . Точки перетину проекціюючих площин з відповідними осями позначені А_Х , А _Y , А _Z .

На комплексному кресленні лінії проекційного Проекціюючі промені АА ₁ , АА ₂ та АА ₃ проводять перпендикулярно відповідним площинам проекцій й отримують проекції точки А : горизонтальну А ₁ , фронтальну А ₂ та профільну А ₃ . Точки перетину проекціюючих площин з відповідними осями позначені А_Х , А _Y , А _Z .

На комплексному кресленні лінії проекційного зв’язку ^ осям координат. Лінія А₁ А ₂ ^Ох розташована вертикально, а А ₂ А ₃ ^О z – горизонтально. При побудові лінії проекційного зв’язку від А₁ до А ₃ необхідно зберігати рівність координатних відрізків по осі Оу : А_Х А₁ = А _Z А ₃

Для переходу до просторову модель розрізають по вісі Оу та суміщають всі три площини проекцій в одну: π₁ обертають навколо вісіπ₃ обертають навколо вісі О z до їх спів падання з π₂ .Вісь Оу розпадається на дві вісі у ₁ та у ₃

Перпендикуляр АА₁ називається горизонтально-проекціюючим, АА₂ - фронтально-проекціюючим і АА₃ - профільно-проекціюючим променем.

На комплексному кресленні чисельні значення координат відкладаються вздовж відповідних координатних осей. Кожна проекція точки визначається двома координатами: горизонтальна – Х_А та Y _А , фронтальна – Х_А та Z _А , профільна – Y _А та Z _А .

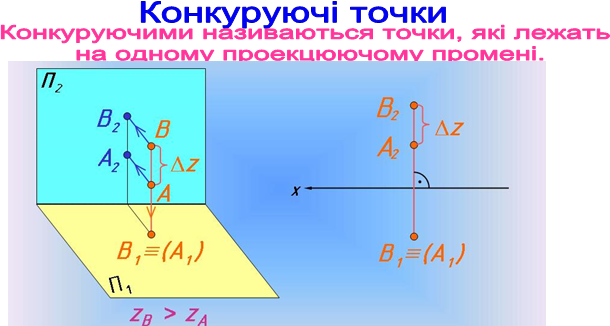Горизонтально конкуруючі точки А та В лежать на одному горизонтально – проекціюючому промені, тому їх горизонтальні проекції співпадають. Точка В віща за точку А та розташована ближче до спостерігача, тому горизонтальна проекція В₁ буде видимою.

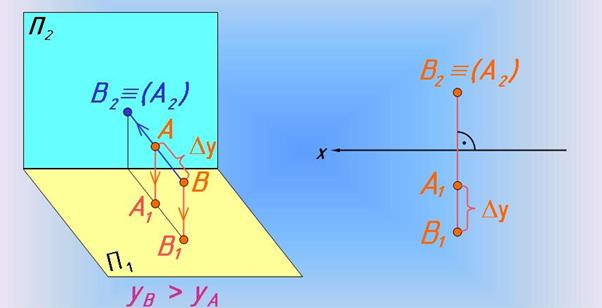
Фронтально конкуруючі точки А та В відрізняються координатою у , лежать на одному фронтально – проекціюючому промені, тому їх фронтальні проекції співпадають. Ближче до спостерігача розташована точка В , тому її фронтальна проекція В₂ буде видимою.

До сих пір ми розглядали проекції точки, а зараз розглянемо комплексне креслення лінії. Пряма в просторі безмежна. Обмежена частина прямої називається відрізком.

По розташуванню відносно площин проекцій прямі можуть бути загального та частинного положень.

Прямою загального положення є пряма, яка не паралельна жодній з площин проекцій.

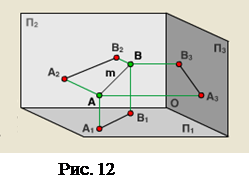Розглянемо схему побудови ортогонального креслення прямої лінії. Проекціювання прямої зводиться до побудови проекцій будь-яких двох її точок, так як дві точки повністю визначають положення прямої в просторі.

Наприклад візьмемо пряму mзагального положення (рис. 12), яка задана двома точками А і В.Побудуємо ортогональні проекції відрізку АВ на площинах π₁ ,π₂ , π₃ . З’єднаємо проекції точок А і В на кожній площині отримаємо проекцію відрізку АВ на всі три проекціюючі площини.

Комплексне креслення відрізку прямої АВ загального положення на всі три площини проекції наведено на рис. 13.

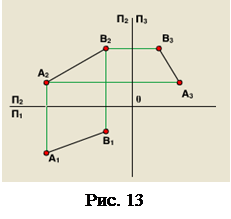
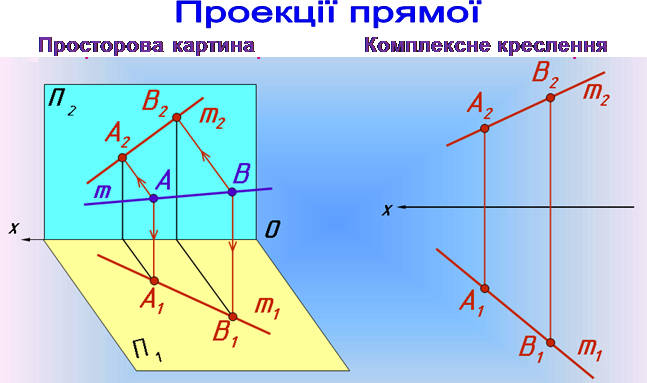
Положення прямої m в просторі визначають дві довільні точки А та В , які лежать на цій прямій. Пряма лінія m є заданою, якщо на комплексному кресленні побудувати проекції двох її точок А та В . Проекції прямої m проходять через пари відповідних проекцій точок: горизонтальна проекція прямої m ₁ – через А₁ та В₁ ; фронтальна проекція прямої m ₂ – через А₂ та В₂

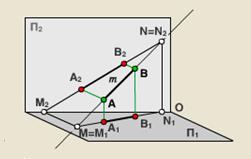
Якщо відрізок АВ загального положення (рис. 14) продовжити в обидва боки від точок А і В, то в точках М і N він перетне площини проекцій π₁ і π₂ .

Рис. 14

Пряма, яка паралельна якій-небудь площині проекцій, не може мати сліду на тій площині, якій вона паралельна, так як вона з нею не перетинається.

Пряма частинного положення (або пряма рівня) – називається пряма, паралельна хоч би одній з площин проекцій.

Проекціюючими називаються прямі, перпендикулярні до однієї з площин проекцій, тобто паралельні двом іншим площинам.

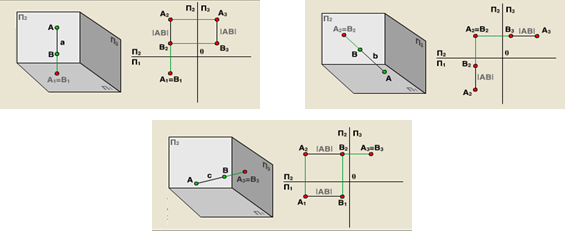Рис. 16

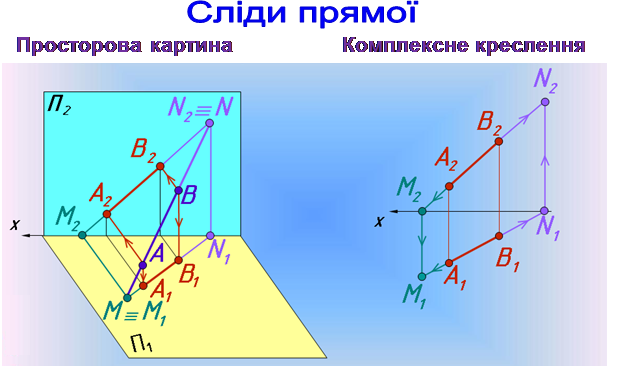
Слід прямої – це точка перетину прямої з відповідною площиною проекцій.Точка М — горизонтальний слід прямої АВ ,вона має аплікатуz _М = 0, а точка N - фронтальний слід прямої АВ ,вона має аплікатуy_N = 0.

Для побудови горизонтального сліду прямої АВ знайдемо на ній точку М з координатою z = 0, перетин фронтальної проекції прямої А ₂ В ₂ з віссю х визначає фронтальну проекцію сліду М ₂ . Горизонтальна проекція сліду М₁ належить горизонтальній проекції прямої.

Для побудови фронтального сліду прямої АВ знайдемо на ній точку N з координатою у = 0, перетин горизонтальної проекції прямої А ₁ В ₁ з віссю х визначає горизонтальну проекцію сліду N ₁ . Фронтальна проекція сліду N ₂ належить фронтальній проекції прямої.