Название: Обусловленность матрицы

Вид работы: контрольная работа

Рубрика: Математика

Размер файла: 138.66 Kb

Скачать файл: referat.me-215955.docx

Краткое описание работы: Исследование зависимости погрешности решения от погрешностей правой части системы. Определение корня уравнения с заданной точностью. Вычисление точностных оценок методов по координатам. Сплайн интерполяция и решение дифференциального уравнения.

Обусловленность матрицы

Министерство образования и науки российской федерации

Федеральное агентство по образованию

Новосибирский государственный технический университет

Бердский филиал

Расчетно-графическая работа

по курсу: «Вычислительная математика»

Выполнила:

Студентка II курса

Булгакова Н.

Группы ВТБ-81

Проверил:

Преподаватель

Голубева Елена Николаевна

г.362964Бердск,

2010

Задание 1 Обусловленность матрицы

Задание: Дана система уравнений ax=b порядка n. Исследовать зависимость погрешности решения x от погрешностей правой части системы b.

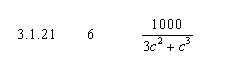
погрешность уравнение координата интерполяция дифференциальный

1. Задать матрицу системы A и вектор правой части b, найти решение x системы Ax=b с помощью метода Гаусса.

2. Принимая решение x, полученное в п.1, за точное, вычислить вектор

относительных погрешностей решений систем ,где компоненты векторов вычисляются по формулам:

(-произвольная величина погрешности).

3. На основе вычисленного вектора d построить гистограмму. По гистограмме определить компоненту , вектора b, которая оказывает наибольшее влияние на погрешность решения.

4. Вычислить число обусловленности cond(A) матрицы A.

5. Оценить теоретически погрешность решения по формуле:

Сравнить значение со значением практической погрешности Объяснить полученные результаты.

Решение

1. Задаём матрицу А.

Для заполнения используем код программы zapolnenie . cpp (см. приложение)

#include <iostream.h>

#include <stdio.h>

#include <conio.h>

#include <math.h>

#include <windows.h>

#include <dos.h>

main()

{

double matr[100][100];

for (int i=1;i<7;i++)

{

for (int j=1;j<7;j++)

matr[i][j]= 1000/(3*(pow(0.1*21*i*j,2))+pow(0.1*21*i*j,3));

}

for ( int j=1;j<7;j++)

{

for ( int i=1;i<7;i++)

printf("%10.4f",matr[j][i]);

printf("n");

}

getchar();

}

Результатработы zapolnenie:

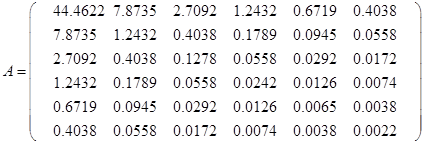
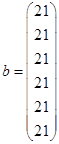
Найдем решение полученной матрицы используя программу gauss . cpp (см приложение)

Исходныйкодgauss.cpp:

#include <iostream.h>

#include <stdio.h>

#include <windows.h>

#include <math.h>

#include <conio.h>

#include <dos.h>

const int sz=6;

double A[sz][sz]={

{44.4622, 7.8735, 2.7092, 1.2432, 0.6719, 0.4038},

{7.8735, 1.2432, 0.4038, 0.1789, 0.0945, 0.0558},

{2.7092, 0.4038, 0.1278, 0.0558, 0.0292, 0.0172},

{1.2432, 0.1789, 0.0558, 0.0242, 0.0126, 0.0074},

{0.6719, 0.0945, 0.0292, 0.0126, 0.0065, 0.0038},

{0.4038, 0.0558, 0.0172, 0.0074, 0.0038, 0.0022}

} ;

double F[sz]={21.00,21.00,21.00,21.00,21.00,21.00} ;

double X[sz];

double b[sz+1],par;

// функция вывода матрицы на экран

voidViv(doubleA[sz][sz])

{

int i,j;

for( i=0;i<sz; i++)

{

for( j=0;j<sz; j++)

printf(" %.4f ",A[i][j]); //вывод на экрам исходной матрицы с заданным количеством знаков после запятой (5f)

printf(" %.4f ",F[i]);

cout<<endl;

}

system("pause");

}

/////////////// функция решения методом Гаусса

void Resh(double A[sz][sz],double F[sz],double X[sz])

{

int i,j,k;

for (k=0;k<sz;k++)

{

// проверяем первый элемент

if (A[k][k]==0) //проверка на неноль

{

for (i=k;A[i][k]==0;i++); // находим ненулевой 1й элемент

for(j=k;j<sz;j++) // меняем строки в матрице

{

par=A[k][j]; //смена строк в матрице

A[k][j]=A[i][j]; //путем записи в par и извлечения из него

A[i][j]=par;

}

par=F[k]; // смена строк в ответе

F[k]=F[i];

F[i]=par;

}

// получаем 1й элемент единицу (делим всю первую строку на a1,1 )

par=A[k][k]; //пишем в par первый элемент

for(int i=k;i<sz;i++)

A[k][i]=A[k][i]/par;

F[k]=F[k]/par; // делимответна 1й

// нулевойстолбец

for(int j=k+1;j<sz;j++)

{

for(int i=k;i<sz;i++)

b[i]=A[k][i]*A[j][k];

b[sz]= F[k]*A[j][k];

for(int i=k;i<sz;i++)

A[j][i]-=b[i];

F[j]-=b[sz];

}

}

for(i=sz-1;i>=0;i--) //обратка

{

par=0;

for (j=0;j<sz-1-i;j++)

par+=A[i][sz-j-1]*X[sz-1-j];

X[i]=F[i]-par;

}

}

//функция - точка входа в программу

void main()

{

Viv(A); // выводим матрицу

Resh(A,F,X); // решаем матрицу A методом Гаусса

for(int i=0;i<sz;i++) printf("nX[%d]= %.5f nr",i,X[i]); // выводрезультата

system("pause");

}

Результат работы gauss :

====================================================

точное

====================================================

44.4622 7.8735 2.7092 1.2432 0.6719 0.4038 21.0000

7.8735 1.2432 0.4038 0.1789 0.0945 0.0558 21.0000

2.7092 0.4038 0.1278 0.0558 0.0292 0.0172 21.0000

1.2432 0.1789 0.0558 0.0242 0.0126 0.0074 21.0000

0.6719 0.0945 0.0292 0.0126 0.0065 0.0038 21.0000

0.4038 0.0558 0.0172 0.0074 0.0038 0.0022 21.0000

Для продолжения нажмите любую клавишу . . .

X[0]= 872.15582

X[1]= -16329.24792

X[2]= 10011.59140

X[3]= 111650.80126

X[4]= -26697.87796

X[5]= -144076.29603

Для продолжения нажмите любую клавишу . . .

======================================================

2. Вычисляем вектор d.

Величина погрешности, вносимой в правую часть системы – 1%.

Сформируем векторы b (по заданному закону)

b1	b2	b3	b4	b5	b6
20,79	21	21	21	21	21
21	20,79	21	21	21	21
21	21	20,79	21	21	21
21	21	21	20,79	21	21
21	21	21	21	20,79	21
21	21	21	21	21	20,79

Для каждого из них найдем решение матрицы, используя gauss

С погрешностью в …. компоненте

======================================================

в первой

======================================================

44.4622 7.8735 2.7092 1.2432 0.6719 0.4038 20.7900

7.8735 1.2432 0.4038 0.1789 0.0945 0.0558 21.0000

2.7092 0.4038 0.1278 0.0558 0.0292 0.0172 21.0000

1.2432 0.1789 0.0558 0.0242 0.0126 0.0074 21.0000

0.6719 0.0945 0.0292 0.0126 0.0065 0.0038 21.0000

0.4038 0.0558 0.0172 0.0074 0.0038 0.0022 21.0000

Для продолжения нажмите любую клавишу . . .

X[0]= 872.07580

X[1]= -16327.25169

X[2]= 10005.24500

X[3]= 111652.84781

X[4]= -26679.82743

X[5]= -144100.68447

Для продолжения нажмите любую клавишу . . .

======================================================

во второй

======================================================

44.4622 7.8735 2.7092 1.2432 0.6719 0.4038 21.0000

7.8735 1.2432 0.4038 0.1789 0.0945 0.0558 20.7900

2.7092 0.4038 0.1278 0.0558 0.0292 0.0172 21.0000

1.2432 0.1789 0.0558 0.0242 0.0126 0.0074 21.0000

0.6719 0.0945 0.0292 0.0126 0.0065 0.0038 21.0000

0.4038 0.0558 0.0172 0.0074 0.0038 0.0022 21.0000

Для продолжения нажмите любую клавишу . . .

X[0]= 874.15205

X[1]= -16398.19981

X[2]= 10378.69292

X[3]= 111250.49388

X[4]= -27254.14851

X[5]= -143256.57148

Для продолжения нажмите любую клавишу . . .

======================================================

в третьей

======================================================

44.4622 7.8735 2.7092 1.2432 0.6719 0.4038 21.0000

7.8735 1.2432 0.4038 0.1789 0.0945 0.0558 21.0000

2.7092 0.4038 0.1278 0.0558 0.0292 0.0172 20.7900

1.2432 0.1789 0.0558 0.0242 0.0126 0.0074 21.0000

0.6719 0.0945 0.0292 0.0126 0.0065 0.0038 21.0000

0.4038 0.0558 0.0172 0.0074 0.0038 0.0022 21.0000

Для продолжения нажмите любую клавишу . . .

X[0]= 865.80942

X[1]= -15962.14640

X[2]= 7652.50187

X[3]= 114149.98680

X[4]= -23271.06118

X[5]= -148104.07985

Для продолжения нажмите любую клавишу . . .

======================================================

в четвёртой

======================================================

44.4622 7.8735 2.7092 1.2432 0.6719 0.4038 21.0000

7.8735 1.2432 0.4038 0.1789 0.0945 0.0558 21.0000

2.7092 0.4038 0.1278 0.0558 0.0292 0.0172 21.0000

1.2432 0.1789 0.0558 0.0242 0.0126 0.0074 20.7900

0.6719 0.0945 0.0292 0.0126 0.0065 0.0038 21.0000

0.4038 0.0558 0.0172 0.0074 0.0038 0.0022 21.0000

Для продолжения нажмите любую клавишу . . .

X[0]= 874.20237

X[1]= -16729.55530

X[2]= 12510.77695

X[3]= 111600.37766

X[4]= -35532.05319

X[5]= -138409.12992

Для продолжения нажмите любую клавишу . . .

======================================================

в пятой

======================================================

44.4622 7.8735 2.7092 1.2432 0.6719 0.4038 21.0000

7.8735 1.2432 0.4038 0.1789 0.0945 0.0558 21.0000

2.7092 0.4038 0.1278 0.0558 0.0292 0.0172 21.0000

1.2432 0.1789 0.0558 0.0242 0.0126 0.0074 21.0000

0.6719 0.0945 0.0292 0.0126 0.0065 0.0038 20.7900

0.4038 0.0558 0.0172 0.0074 0.0038 0.0022 21.0000

Для продолжения нажмите любую клавишу . . .

X[0]= 890.20635

X[1]= -16885.51847

X[2]= 13438.40819

X[3]= 102816.62603

X[4]= -16375.93145

X[5]= -148185.68530

Для продолжения нажмите любую клавишу . . .

======================================================

в шестой

=====================================================

44.4622 7.8735 2.7092 1.2432 0.6719 0.4038 21.0000

7.8735 1.2432 0.4038 0.1789 0.0945 0.0558 21.0000

2.7092 0.4038 0.1278 0.0558 0.0292 0.0172 21.0000

1.2432 0.1789 0.0558 0.0242 0.0126 0.0074 21.0000

0.6719 0.0945 0.0292 0.0126 0.0065 0.0038 21.0000

0.4038 0.0558 0.0172 0.0074 0.0038 0.0022 20.7900

Для продолжения нажмите любую клавишу . . .

X[0]= 847.76738

X[1]= -15509.52337

X[2]= 5983.80758

X[3]= 117317.96737

X[4]= -30807.26724

X[5]= -140960.86219

Для продолжения нажмите любую клавишу . . .

На основе полученных значений сформируем вектор d

РЕШЕНИЯ С ПОГРЕШНОСТЯМИ
точное	в первой	во втророй	в третьей	в четвёртой	в пятой	в шестой
872,1558	872,0758	874,1521	865,8094	874,2024	890,2064	847,7674
-16329,2479	-16327,2517	-16398,1998	-15962,1464	-16729,5553	-16885,5185	-15509,5234
10011,5914	10005,2450	10378,6929	7652,5019	12510,7770	13438,4082	5983,8076
111650,8013	111652,8478	111250,4939	114149,9868	111600,3777	102816,6260	117317,9674
-26697,8780	-26679,8274	-27254,1485	-23271,0612	-35532,0532	-16375,9315	-30807,2672
-144076,2960	-144100,6845	-143256,5715	-148104,0799	-138409,1299	-148185,6853	-140960,8622
x-xi
||x||	0,0800	1,9962	6,3464	2,0466	18,0505	24,3884
111650,8013	1,9962	68,9519	367,1015	400,3074	556,2705	819,7245
6,3464	367,1015	2359,0895	2499,1856	3426,8168	4027,7838
2,0466	400,3074	2499,1855	50,4236	8834,1752	5667,1661
18,0505	556,2705	3426,8168	8834,1752	10321,9465	4109,3893
24,3884	819,7245	4027,7838	5667,1661	4109,3893	3115,4338
||x-xi|| i:1…6	d
24,3884	0,000218435
819,7245	0,00734186
4027,7838	0,036074831
8834,1752	0,079123259
10321,9465	0,092448477
5667,1661	0,050757953

(см. файл «Вектор и гистограмма.xls»)

Отсюда видим, что

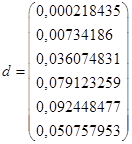
Строим гистограмму элементов вектора относительных погрешностейd. (см. файл «Вектор и гистограмма»)

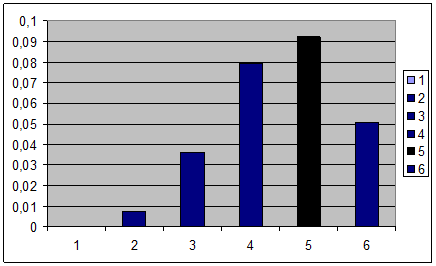
По гистограмме видно, что наибольшее влияние на погрешность решения оказывает компонента вектора .

Найдем число обусловленности матрицы A

Число обусловленности матрицы A вычисляется по формуле

Норма матрицы A: =57,3638

Норма обратной матрицы : =129841,19

7448184,055

Теоретическая оценка погрешности

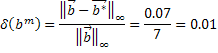
Так как то матрица плохо обусловлена, это значит, что незначительные изменения в правой части приведут к большой погрешности в решении.

Задача 2 Метод хорд

Методом хорд найти корень уравнения с точностью .

Решение

Найдем интервал, в котором находится корень:

Корнем уравнения является точка пересечения этих функций

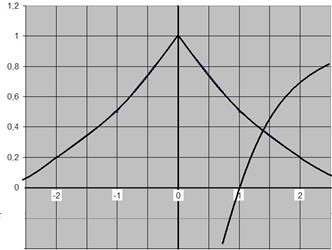
Из графика видно, что корень лежит в интервале .

Найдем неподвижный конец:

Для определения используем horda.xls(см. приложение)

y(a)	-0,5	y(b)	0,493147	непод
y'(a)	1,5	y'(b)	0,66	1
y''(a)	-1,75	y''(b)	-0,426

Неподвижный конец -1

Выполняем приближение, используя horda.xls

Х	х0
1	2
xi	F(xi)	sigma
1,50345005	0,1010481	else
1,41881012	0,0179259	else
1,40431471	0,0030870	else
1,40183381	0,0005288	else
1,40140927	0,0000905	else
1,40133662	0,0000155	else
1,40132419	0,0000027	and

Окончание процесса – при ,это и есть наш корень.

Задача 3 Решение СЛАУ

Решить систему уравнений ax=b, где

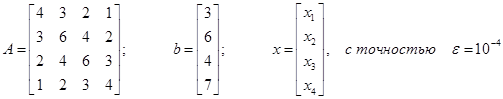
Вычислить точностные оценки методов по координатам: , - координаты численного решения, - координаты точного решения.

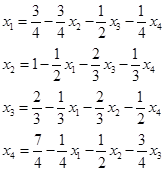
1. Метод простых итераций

Сделаем расчет, используя SLAU.xls

х1	0,7500	-0,7500	-0,3333	-0,4375	-0,7708	0,7500
х2	1,0000	-0,3750	-0,4444	-0,5833	-0,4028	1,0000	1
х3	0,6667	-0,2500	-0,6667	-0,8750	-1,1250	0,6667
х4	1,7500	-0,1875	-0,5000	-0,5000	0,5625	1,7500

х1	0,7500	0,3021	0,5625	-0,1406	1,4740	-0,7708
х2	1,0000	0,3854	0,7500	-0,1875	1,9479	-0,4028	2
х3	0,6667	0,2569	0,2685	-0,2813	0,9109	-1,1250
х4	1,7500	0,1927	0,2014	0,8438	2,9879	0,5625

х1	0,7500	-1,4609	-0,4555	-0,7470	-1,9134	1,4740
х2	1,0000	-0,7370	-0,6073	-0,9960	-1,3402	1,9479	3
х3	0,6667	-0,4913	-1,2986	-1,4940	-2,6172	0,9109
х4	1,7500	-0,3685	-0,9740	-0,6832	-0,2756	2,9879

х1	0,7500	1,0052	1,3086	0,0689	3,1327	-1,9134
х2	1,0000	0,9567	1,7448	0,0919	3,7934	-1,3402	4
х3	0,6667	0,6378	0,8935	0,1378	2,3357	-2,6172
х4	1,7500	0,4784	0,6701	1,9629	4,8614	-0,2756

Решение, наиболее близкое к точному, получено из таблицы 3

Х1=1,4740

Х2=1,9479

Х3=0,9109

Х4=2,9879

Найдём:

xi	xi*	|xi-xi*|
0	1,474	1,474
1	1,9479	0,9479
-1	0,9109	1,9109
2	2,9879	0,9879
max	1,9109

(МПИ)=1,9109

2. Метод Зейделя

Сделаем расчет, используя SLAU.xls

х1	0,7500	0,0000	0,0000	0,0000	0,7500	0,0000
х2	1,0000	-0,3750	0,0000	0,0000	0,6250	0,0000	1
х3	0,6667	-0,2500	0,0000	0,0000	0,4167	0,0000
х4	1,7500	-0,1875	-0,3125	-0,3125	0,9375	0,0000

х1	0,7500	-0,4688	-0,2084	-0,2344	-0,1615	0,7500
х2	1,0000	0,0807	-0,2778	-0,3125	0,4904	0,6250	2
х3	0,6667	0,0538	-0,4167	-0,4688	-0,1649	0,4167
х4	1,7500	0,0404	-0,2452	0,1237	1,6688	0,9375

х1	0,7500	-0,7499	0,5000	-0,5000	0,0000	0,0000
х2	1,0000	0,0000	0,6666	-0,6667	0,9999	0,9999	30
х3	0,6667	0,0000	-0,6666	-1,0000	-0,9999	-0,9999
х4	1,7500	0,0000	-0,5000	0,7500	2,0000	2,0000

Решение, наиболее близкое к точному, получено на 30 шаге вычислений

Х1=0

Х2=0,9999

Х3=0,9999

Х4=2

Найдём:

xi	xi*	|xi-xi*|
0	0,0000	0,0000
1	0,9999	-0,0001
-1	-0,9999	0,0001
2	2,0000	0,0000
max	0,0001

=0,0001

Вывод: МПИ - быстрее сходится, но обладает меньшей точностью, чем метод Зейделя, который дольше сходится.

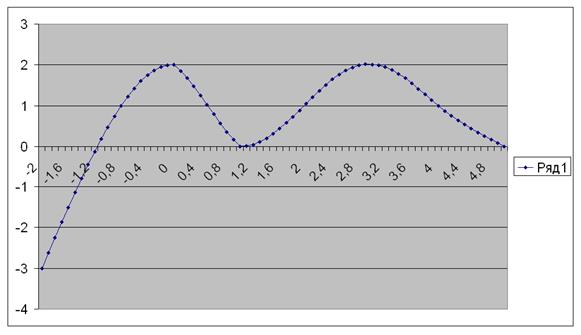
Задача 4 Сплайн интерполяция

Х	У
-2,00	-3,00
0,00	2,00
1,00	0,00
3,00	2,00
4,00	1,00
5,00	0,00

Для вычислений используем splain.xls

Найдем :

hi=xi - xi-1
h0	2,00
h1	1,00
h2	2,00
h3	1,00
h4	1,00

Для вычисления q будем использовать метод прогонки.

Вычислим массивы коэффициентов a,b,c и правой части d:

a	b	c	d
0	0,0000	1,0000	0,1667	-4,50
1	0,1667	1,0000	0,3333	3,00
2	0,3333	1,0000	0,1667	-2,00
3	0,1667	0,6667	0,0000	0,00

Вычисление прогоночных коэффициентов:

A[ ]	B[ ]
0,00	0,00
-0,16667	-4,5
-0,34286	3,857143
-0,18817	-3,70968
0	0,973202

Теперь вычисляем

x	y
-2	-3
-1,9	-2,62093
-1,8	-2,24381
-1,7	-1,87056
-1,6	-1,50314
-1,5	-1,14348
-1,4	-0,79353
-1,3	-0,45522
-1,2	-0,13049
-1,1	0,178702
-1	0,47043
-0,9	0,74275
-0,8	0,99372
-0,7	1,221401
-0,6	1,423849
-0,5	1,599126
-0,4	1,74529
-0,3	1,860401
-0,2	1,942516
-0,1	1,989696
0	2
0,1	1,852492
0,2	1,673571
0,3	1,470644
0,4	1,251116
0,5	1,02239
0,6	0,791874
0,7	0,566972
0,8	0,355088
0,9	0,163629
1	0
1,1	0,005772
1,2	0,043163
1,3	0,108555
1,4	0,198332
1,5	0,308877
1,6	0,436575
1,7	0,577807
1,8	0,728958
1,9	0,886412
2	1,046551
2,1	1,205759
2,2	1,360419
2,3	1,506916
2,4	1,641631
2,5	1,760949
2,6	1,861253
2,7	1,938927
2,8	1,990354
2,9	2,011917
3	2
3,1	1,989668
3,2	1,946922
3,3	1,876445
3,4	1,78292
3,5	1,67103
3,6	1,545457
3,7	1,410885
3,8	1,271996
3,9	1,133473
4	1
4,1	0,872264
4,2	0,753286
4,3	0,642094
4,4	0,537715
4,5	0,439175
4,6	0,345501
4,7	0,255719
4,8	0,168858
4,9	0,083942
5	0

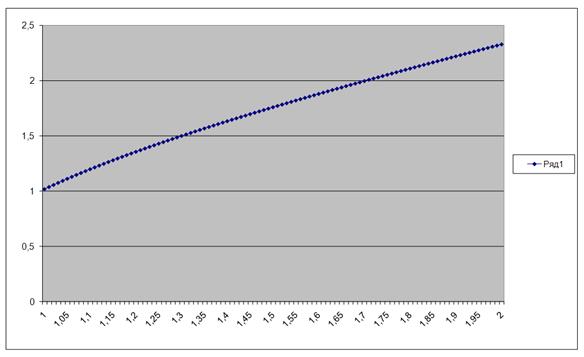
Задача 5 Решение дифференциального уравнения

Для расчета использован файл diffur.xls

Мы выбираем шаг h, рассчитываем значения для точки х+2h с шагом h и 2h, если проверка на окончание процесса показала < δ, то берем шаг h и считаем с ним остальные точки, если же нет – берем новое h и снова делаем проверку

{1,2}	x	y	k1	0,00004000	k2	0,00004000	k3	0,00004000	k4	0,00004000
y(1)=1	1	1
1,00001	1,00002	∆y	0,00004000	y1	1,00004000
1,00001	1,00002
1,00002	1,00004
0,00002
x	y	k1	0,00004018	k2	0,00004018	k3	0,00004018	k4	0,00004018
1,1	1,00004
1,10001	1,00006	∆y	0,00004018	y2	1,00008018
1,10001	1,00006
1,10002	1,00008
0,00002
x	y	k1	0,00004066	k2	0,00004066	k3	0,00004066	k4	0,00004066
1,2	1,00008
1,20001	1,000101	∆y	0,00004066	y2	1,00012084
1,20001	1,000101
1,20002	1,000121

{1,2}	x	y	k1	0,000080000	k2	0,000079997	k3	0,000079997	k4	0,000079994
y(1)=1	1	1
1,00002	1,00004	∆y	0,000079997	y1	1,000079997
1,00002	1,00004
1,00004	1,00008
0,00004
x	y	k1	0,000081327	k2	0,000081324	k3	0,000081324	k4	0,000081321
1,2	1,00008
1,20002	1,000121	∆y	0,000081324	y2	1,000161321
1,20002	1,000121
1,20004	1,000161
0,00004
x	y	k1	0,000084558	k2	0,000084555	k3	0,000084555	k4	0,000084551
1,4	1,000161
1,40002	1,000204	∆y	0,000084555	y2	1,000245875
1,40002	1,000204
1,40004	1,000246

R=0,000008 <0,00001Процесс закончен – шаг = 0,00004 Для наглядности возьмем шаг = 0,01

xk1	xk2	xk3	xk4	y	k1	yk2	k2	yk3	k3	yk4	k4	∆y	y
1	1,005	1,005	1,01	1	0,02	1,01	0,019802	1,009901	0,019804	1,019804	0,019613	0,019804	1,019804
1,01	1,015	1,015	1,02	1,019804	0,019613	1,029611	0,019427	1,029518	0,019429	1,039233	0,019249	0,019429	1,039233
1,02	1,025	1,025	1,03	1,039233	0,019249	1,048857	0,019074	1,04877	0,019076	1,058309	0,018906	0,019076	1,058309
1,03	1,035	1,035	1,04	1,058309	0,018906	1,067762	0,018742	1,06768	0,018743	1,077052	0,018583	0,018743	1,077052
1,04	1,045	1,045	1,05	1,077052	0,018583	1,086344	0,018428	1,086266	0,01843	1,095482	0,018279	0,01843	1,095482
1,05	1,055	1,055	1,06	1,095482	0,018279	1,104621	0,018132	1,104548	0,018133	1,113615	0,01799	0,018133	1,113615
1,06	1,065	1,065	1,07	1,113615	0,01799	1,12261	0,017851	1,12254	0,017852	1,131467	0,017717	0,017852	1,131467
1,07	1,075	1,075	1,08	1,131467	0,017717	1,140325	0,017585	1,140259	0,017586	1,149053	0,017457	0,017586	1,149053
1,08	1,085	1,085	1,09	1,149053	0,017457	1,157781	0,017332	1,157719	0,017333	1,166386	0,017211	0,017333	1,166386
1,09	1,095	1,095	1,1	1,166386	0,017211	1,174991	0,017092	1,174931	0,017092	1,183478	0,016976	0,017092	1,183478
1,1	1,105	1,105	1,11	1,183478	0,016976	1,191966	0,016863	1,191909	0,016864	1,200342	0,016753	0,016864	1,200342
1,11	1,115	1,115	1,12	1,200342	0,016753	1,208718	0,016645	1,208664	0,016645	1,216987	0,01654	0,016645	1,216987
1,12	1,125	1,125	1,13	1,216987	0,01654	1,225257	0,016436	1,225205	0,016437	1,233424	0,016336	0,016437	1,233424
1,13	1,135	1,135	1,14	1,233424	0,016336	1,241592	0,016238	1,241543	0,016238	1,249663	0,016142	0,016238	1,249663
1,14	1,145	1,145	1,15	1,249663	0,016142	1,257734	0,016048	1,257686	0,016048	1,265711	0,015956	0,016048	1,265711
1,15	1,155	1,155	1,16	1,265711	0,015956	1,273689	0,015866	1,273644	0,015866	1,281577	0,015778	0,015866	1,281577
1,16	1,165	1,165	1,17	1,281577	0,015778	1,289466	0,015692	1,289423	0,015692	1,297269	0,015607	0,015692	1,297269
1,17	1,175	1,175	1,18	1,297269	0,015607	1,305073	0,015525	1,305032	0,015525	1,312794	0,015444	0,015525	1,312794
1,18	1,185	1,185	1,19	1,312794	0,015444	1,320516	0,015364	1,320476	0,015365	1,328159	0,015287	0,015365	1,328159
1,19	1,195	1,195	1,2	1,328159	0,015287	1,335803	0,01521	1,335764	0,015211	1,34337	0,015136	0,015211	1,34337
1,2	1,205	1,205	1,21	1,34337	0,015136	1,350938	0,015063	1,350901	0,015063	1,358433	0,014991	0,015063	1,358433
1,21	1,215	1,215	1,22	1,358433	0,014991	1,365929	0,014921	1,365893	0,014921	1,373354	0,014852	0,014921	1,373354
1,22	1,225	1,225	1,23	1,373354	0,014852	1,38078	0,014784	1,380746	0,014784	1,388138	0,014718	0,014784	1,388138
1,23	1,235	1,235	1,24	1,388138	0,014718	1,395497	0,014652	1,395465	0,014653	1,402791	0,014588	0,014653	1,402791
1,24	1,245	1,245	1,25	1,402791	0,014588	1,410085	0,014525	1,410054	0,014526	1,417317	0,014464	0,014526	1,417317
1,25	1,255	1,255	1,26	1,417317	0,014464	1,424549	0,014403	1,424518	0,014404	1,43172	0,014344	0,014404	1,43172
1,26	1,265	1,265	1,27	1,43172	0,014344	1,438892	0,014285	1,438863	0,014286	1,446006	0,014228	0,014286	1,446006
1,27	1,275	1,275	1,28	1,446006	0,014228	1,45312	0,014172	1,453092	0,014172	1,460178	0,014116	0,014172	1,460178
1,28	1,285	1,285	1,29	1,460178	0,014116	1,467236	0,014062	1,467209	0,014062	1,47424	0,014009	0,014062	1,47424
1,29	1,295	1,295	1,3	1,47424	0,014009	1,481245	0,013956	1,481218	0,013956	1,488196	0,013904	0,013956	1,488196
1,3	1,305	1,305	1,31	1,488196	0,013904	1,495149	0,013853	1,495123	0,013854	1,50205	0,013804	0,013854	1,50205
1,31	1,315	1,315	1,32	1,50205	0,013804	1,508952	0,013754	1,508927	0,013755	1,515805	0,013706	0,013755	1,515805
1,32	1,325	1,325	1,33	1,515805	0,013706	1,522658	0,013658	1,522634	0,013659	1,529463	0,013612	0,013659	1,529463
1,33	1,335	1,335	1,34	1,529463	0,013612	1,536269	0,013566	1,536246	0,013566	1,543029	0,013521	0,013566	1,543029
1,34	1,345	1,345	1,35	1,543029	0,013521	1,54979	0,013476	1,549767	0,013476	1,556505	0,013432	0,013476	1,556505
1,35	1,355	1,355	1,36	1,556505	0,013432	1,563222	0,013389	1,5632	0,013389	1,569895	0,013347	0,013389	1,569895
1,36	1,365	1,365	1,37	1,569895	0,013347	1,576568	0,013305	1,576547	0,013305	1,5832	0,013264	0,013305	1,5832
1,37	1,375	1,375	1,38	1,5832	0,013264	1,589832	0,013223	1,589811	0,013223	1,596423	0,013183	0,013223	1,596423
1,38	1,385	1,385	1,39	1,596423	0,013183	1,603015	0,013144	1,602995	0,013144	1,609567	0,013106	0,013144	1,609567
1,39	1,395	1,395	1,4	1,609567	0,013106	1,61612	0,013067	1,616101	0,013068	1,622635	0,01303	0,013068	1,622635
1,4	1,405	1,405	1,41	1,622635	0,01303	1,62915	0,012993	1,629132	0,012993	1,635628	0,012957	0,012993	1,635628
1,41	1,415	1,415	1,42	1,635628	0,012957	1,642106	0,012921	1,642088	0,012921	1,648549	0,012885	0,012921	1,648549
1,42	1,425	1,425	1,43	1,648549	0,012885	1,654992	0,012851	1,654974	0,012851	1,6614	0,012816	0,012851	1,6614
1,43	1,435	1,435	1,44	1,6614	0,012816	1,667808	0,012782	1,667791	0,012783	1,674182	0,012749	0,012783	1,674182
1,44	1,445	1,445	1,45	1,674182	0,012749	1,680557	0,012716	1,68054	0,012716	1,686899	0,012684	0,012716	1,686899
1,45	1,455	1,455	1,46	1,686899	0,012684	1,693241	0,012652	1,693225	0,012652	1,699551	0,012621	0,012652	1,699551
1,46	1,465	1,465	1,47	1,699551	0,012621	1,705861	0,01259	1,705846	0,01259	1,71214	0,012559	0,01259	1,71214
1,47	1,475	1,475	1,48	1,71214	0,012559	1,71842	0,012529	1,718405	0,012529	1,724669	0,012499	0,012529	1,724669
1,48	1,485	1,485	1,49	1,724669	0,012499	1,730919	0,01247	1,730904	0,01247	1,737139	0,012441	0,01247	1,737139
1,49	1,495	1,495	1,5	1,737139	0,012441	1,743359	0,012412	1,743345	0,012412	1,749551	0,012384	0,012412	1,749551
1,5	1,505	1,505	1,51	1,749551	0,012384	1,755743	0,012356	1,75573	0,012356	1,761908	0,012329	0,012356	1,761908
1,51	1,515	1,515	1,52	1,761908	0,012329	1,768072	0,012302	1,768059	0,012302	1,77421	0,012275	0,012302	1,77421
1,52	1,525	1,525	1,53	1,77421	0,012275	1,780348	0,012249	1,780334	0,012249	1,786459	0,012223	0,012249	1,786459
1,53	1,535	1,535	1,54	1,786459	0,012223	1,79257	0,012197	1,792558	0,012197	1,798656	0,012172	0,012197	1,798656
1,54	1,545	1,545	1,55	1,798656	0,012172	1,804742	0,012147	1,80473	0,012147	1,810804	0,012123	0,012147	1,810804
1,55	1,555	1,555	1,56	1,810804	0,012123	1,816865	0,012098	1,816853	0,012098	1,822902	0,012074	0,012098	1,822902
1,56	1,565	1,565	1,57	1,822902	0,012074	1,828939	0,012051	1,828927	0,012051	1,834953	0,012027	0,012051	1,834953
1,57	1,575	1,575	1,58	1,834953	0,012027	1,840966	0,012004	1,840955	0,012004	1,846957	0,011981	0,012004	1,846957
1,58	1,585	1,585	1,59	1,846957	0,011981	1,852948	0,011959	1,852936	0,011959	1,858916	0,011937	0,011959	1,858916
1,59	1,595	1,595	1,6	1,858916	0,011937	1,864884	0,011915	1,864873	0,011915	1,870831	0,011893	0,011915	1,870831
1,6	1,605	1,605	1,61	1,870831	0,011893	1,876777	0,011872	1,876766	0,011872	1,882702	0,011851	0,011872	1,882702
1,61	1,615	1,615	1,62	1,882702	0,011851	1,888628	0,01183	1,888617	0,01183	1,894532	0,011809	0,01183	1,894532
1,62	1,625	1,625	1,63	1,894532	0,011809	1,900437	0,011789	1,900427	0,011789	1,906321	0,011769	0,011789	1,906321
1,63	1,635	1,635	1,64	1,906321	0,011769	1,912205	0,011749	1,912195	0,011749	1,91807	0,011729	0,011749	1,91807
1,64	1,645	1,645	1,65	1,91807	0,011729	1,923935	0,01171	1,923925	0,01171	1,92978	0,011691	0,01171	1,92978
1,65	1,655	1,655	1,66	1,92978	0,011691	1,935625	0,011672	1,935616	0,011672	1,941452	0,011653	0,011672	1,941452
1,66	1,665	1,665	1,67	1,941452	0,011653	1,947278	0,011635	1,947269	0,011635	1,953087	0,011616	0,011635	1,953087
1,67	1,675	1,675	1,68	1,953087	0,011616	1,958895	0,011598	1,958886	0,011599	1,964685	0,011581	0,011599	1,964685
1,68	1,685	1,685	1,69	1,964685	0,011581	1,970475	0,011563	1,970467	0,011563	1,976248	0,011546	0,011563	1,976248
1,69	1,695	1,695	1,7	1,976248	0,011546	1,982021	0,011528	1,982012	0,011529	1,987777	0,011512	0,011529	1,987777
1,7	1,705	1,705	1,71	1,987777	0,011512	1,993533	0,011495	1,993524	0,011495	1,999272	0,011478	0,011495	1,999272
1,71	1,715	1,715	1,72	1,999272	0,011478	2,005011	0,011462	2,005002	0,011462	2,010733	0,011446	0,011462	2,010733
1,72	1,725	1,725	1,73	2,010733	0,011446	2,016456	0,01143	2,016448	0,01143	2,022163	0,011414	0,01143	2,022163
1,73	1,735	1,735	1,74	2,022163	0,011414	2,02787	0,011398	2,027862	0,011398	2,033561	0,011383	0,011398	2,033561
1,74	1,745	1,745	1,75	2,033561	0,011383	2,039252	0,011367	2,039245	0,011367	2,044928	0,011352	0,011367	2,044928
1,75	1,755	1,755	1,76	2,044928	0,011352	2,050604	0,011337	2,050597	0,011337	2,056265	0,011322	0,011337	2,056265
1,76	1,765	1,765	1,77	2,056265	0,011322	2,061927	0,011308	2,061919	0,011308	2,067573	0,011293	0,011308	2,067573
1,77	1,775	1,775	1,78	2,067573	0,011293	2,07322	0,011279	2,073213	0,011279	2,078852	0,011265	0,011279	2,078852
1,78	1,785	1,785	1,79	2,078852	0,011265	2,084485	0,011251	2,084478	0,011251	2,090103	0,011237	0,011251	2,090103
1,79	1,795	1,795	1,8	2,090103	0,011237	2,095722	0,011223	2,095715	0,011223	2,101327	0,01121	0,011223	2,101327
1,8	1,805	1,805	1,81	2,101327	0,01121	2,106931	0,011196	2,106925	0,011196	2,112523	0,011183	0,011196	2,112523
1,81	1,815	1,815	1,82	2,112523	0,011183	2,118115	0,01117	2,118108	0,01117	2,123693	0,011157	0,01117	2,123693
1,82	1,825	1,825	1,83	2,123693	0,011157	2,129272	0,011144	2,129265	0,011144	2,134838	0,011132	0,011144	2,134838
1,83	1,835	1,835	1,84	2,134838	0,011132	2,140404	0,011119	2,140397	0,011119	2,145957	0,011107	0,011119	2,145957
1,84	1,845	1,845	1,85	2,145957	0,011107	2,15151	0,011095	2,151504	0,011095	2,157052	0,011082	0,011095	2,157052
1,85	1,855	1,855	1,86	2,157052	0,011082	2,162593	0,01107	2,162587	0,01107	2,168122	0,011059	0,01107	2,168122
1,86	1,865	1,865	1,87	2,168122	0,011059	2,173651	0,011047	2,173645	0,011047	2,179169	0,011035	0,011047	2,179169
1,87	1,875	1,875	1,88	2,179169	0,011035	2,184686	0,011024	2,184681	0,011024	2,190193	0,011012	0,011024	2,190193
1,88	1,885	1,885	1,89	2,190193	0,011012	2,195699	0,011001	2,195693	0,011001	2,201194	0,01099	0,011001	2,201194
1,89	1,895	1,895	1,9	2,201194	0,01099	2,206689	0,010979	2,206683	0,010979	2,212173	0,010968	0,010979	2,212173
1,9	1,905	1,905	1,91	2,212173	0,010968	2,217657	0,010957	2,217651	0,010957	2,22313	0,010947	0,010957	2,22313
1,91	1,915	1,915	1,92	2,22313	0,010947	2,228603	0,010936	2,228598	0,010936	2,234066	0,010926	0,010936	2,234066
1,92	1,925	1,925	1,93	2,234066	0,010926	2,239529	0,010915	2,239523	0,010915	2,244981	0,010905	0,010915	2,244981
1,93	1,935	1,935	1,94	2,244981	0,010905	2,250434	0,010895	2,250428	0,010895	2,255876	0,010885	0,010895	2,255876
1,94	1,945	1,945	1,95	2,255876	0,010885	2,261318	0,010875	2,261313	0,010875	2,266751	0,010865	0,010875	2,266751
1,95	1,955	1,955	1,96	2,266751	0,010865	2,272183	0,010855	2,272178	0,010855	2,277606	0,010846	0,010855	2,277606
1,96	1,965	1,965	1,97	2,277606	0,010846	2,283029	0,010836	2,283024	0,010836	2,288442	0,010827	0,010836	2,288442
1,97	1,975	1,975	1,98	2,288442	0,010827	2,293855	0,010817	2,293851	0,010817	2,299259	0,010808	0,010817	2,299259
1,98	1,985	1,985	1,99	2,299259	0,010808	2,304663	0,010799	2,304659	0,010799	2,310058	0,01079	0,010799	2,310058
1,99	1,995	1,995	2	2,310058	0,01079	2,315453	0,010781	2,315449	0,010781	2,320839	0,010772	0,010781	2,320839
2	2,005	2,005	2,01	2,320839	0,010772	2,326225	0,010763	2,326221	0,010763	2,331602	0,010754	0,010763	2,331602