Название: Нелинейное уравнение и интервал изоляции корня
Вид работы: контрольная работа
Рубрика: Математика
Размер файла: 42.52 Kb
Скачать файл: referat.me-217694.docx
Краткое описание работы: Изучение методов уточнения корней нелинейных уравнений (половинного деления, хорд, касательных, простой итерации). Метод хорд и касательных дает высокую скорость сходимости при решении уравнений, и небольшую - метод половинного деления и простой итерации.
Нелинейное уравнение и интервал изоляции корня
Министерство образования РФ
Рязанская государственная радиотехническая академия
Кафедра ОиЭФ
Контрольная работа
«Нелинейное уравнение и интервал изоляции корня»
Выполнил ст. гр. 255
Ампилогов Н. В.
Проверил
Малютин А. Е.
Рязань 2007
Расчетная часть.
I.Заданное нелинейное уравнение и интервал изоляции корня:
.
II.Схема алгоритма отделения корней
Разбиение исходного интервала 
, на котором определена и непрерывна функция 
,на n отрезков равной длины:
Вычисление значения функции 
в точках 
концах отрезка 
Выделение отрезка 
Длина отрезка достаточно мала (можно предположить единственность корня)
|
|
Корень отделен на интервале
Границы исходного отрезка сдвигаются
(
)
Воспользуемся приведенным выше алгоритмом для отделения корня уравнения на заданном отрезке:
1. Разобьем интервал изоляции корня 
на n отрезков равной длины:
2. Вычисляем значения функции в точках 
:
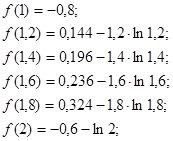
3. На концах отрезка (1;2) функция имеет разные знаки и он достаточно мал для определения корня.
III. Уточнение корня методом половинного деления
Отделение корней, нахождение отрезка изоляции
Вычисление f(a)
=(a+b)/2
Вычисление f()
a=f(a)*f()<0 b=
Вывод
Произведем вычисления согласно представленному выше алгоритму. Необходимо определить корень методом половинного деления с погрешностью
.
Все условия для выполнения данного метода(указаны в теоретической части) выполняются.
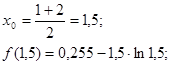
Т.к.f(
)
то выбираем другой отрезок [1;1,5] на концах которого функция имеет разные знаки и продолжаем вычисления.
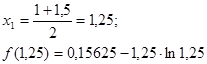
Выбираем отрезок [1;1,25] ,
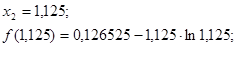
является корнем т.к. нам необходимо найти корень с заданной погрешностью и выполняется условие прекращения вычислений:
;
Мы нашли корень за 2 шага.
Проведем вычисления в системе MathCAD
В системе MathCAD мы нашли корень так же за 2 шага.
IV. Уточнение корня методом хорд.
Отделение корней, нахождение отрезка изоляции.
Вывод
Произведем вычисления согласно представленному выше алгоритму. Необходимо определить корень методом хорд с погрешностью
.
Все условия для выполнения данного метода(указаны в теоретической части) выполняются.
Для того чтобы определить какой формулой метода хорд необходимо воспользоваться найдем значения первой и второй производной на концах отрезка изоляции корня:
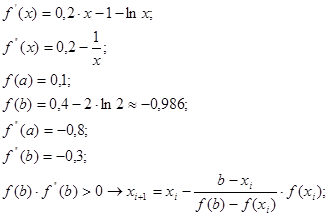
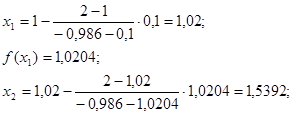
Нашли корень за 1 шаг. Проведем вычисления в системе MathCAD.
В системе MathCAD мы нашли корень за 2 шага, это объясняется более высокой точностью MathCAD по сравнению с расчетами вручную.
V. Уточнение корня методом касательных.
Отделение корней, нахождение отрезка изоляции.
Вывод 
Произведем вычисления согласно представленному выше алгоритму. Необходимо определить корень методом касательных с погрешностью.
Все условия для выполнения данного метода(указаны в теоретической части) выполняются.
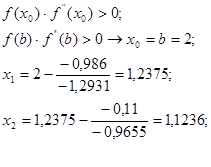
Нашли корень за 2 шага. Проведем вычисления в системе MathCAD.
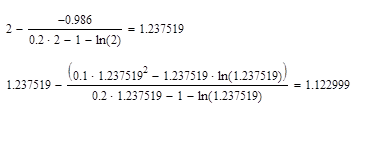
В системе MathCAD мы нашли корень так же за 2 шага.
VI. Уточнение корня методом простой итерации.
Отделение корней, нахождение отрезка изоляции
[c;d]=[a-h;b+h]
Приведение уравнения
f(x)=0 к виду x=g(x)
n=0
n=n+1
Вывод 
Произведем вычисления согласно представленному выше алгоритму. Необходимо определить корень методом простой итерации с погрешностью.
Все условия для выполнения данного метода(указаны в теоретической части) выполняются.
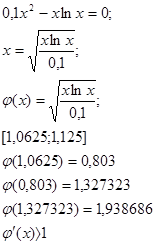
Значит, итерационный процесс не применим, расходится и не позволяет получить решение.
Вывод: Изучили различные методы уточнения корней нелинейных уравнений (метод половинного деления, хорд, касательных, простой итерации). На основе полученных нами результатов можно сделать вывод о том, что высокую скорость сходимости при решении уравнений дает метод хорд и метод касательных. Скорость сходимости методов половинного деления и простой итерации небольшие, но они наиболее легко реализуются на ЭВМ.
Похожие работы
-
Решение нелинейных уравнений
Задание №1 Отделить корни уравнения графически и уточнить один из них: · методом половинного деления; · методом хорд; · методом касательных; · методом секущих;
-
Решение нелинейных уравнений с одной переменной
Раздел 2. Численные методы Тема 1. Решение нелинейных уравнений с одной переменной 1.1. Постановка задачи При решении ряда задач физики, механики и техники возникает необходимость решения уравнений с одной переменной. В общем случае нелинейное уравнение можно записать в виде: F(x)=0, где функция F(x) определена и непрерывна на промежутке {a, b}.
-
Приближённое решение алгебраических и трансцендентных уравнений
Приближённое решение алгебраических и трансцендентных уравнений 1. Общая постановка задачи. Найти действительные корни уравнения , где - алгебраическая или трансцендентная функция.
-
Нахождение корня нелинейного уравнения. Методы решения системы нелинейных уравнений
Приближенные значения корней. Метод дихотомии (или деление отрезка пополам), простой итерации и Ньютона. Метод деления отрезка пополам для решения уравнения. Исследование сходимости метода Ньютона. Построение нескольких последовательных приближений.
-
Решение одного нелинейного уравнения
Методы решения одного нелинейного уравнения: половинного деления, простой итерации, Ньютона, секущих. Код программы решения перечисленных методов на языке программирования Microsoft Visual C++ 6.0. Применение методов к конкретной задаче и анализ решений.
-
Нахождение всех действительных корней алгебраического многочлена методом деления отрезка пополам (бисекции)
В данной курсовой работе рассмотрен принцип нахождения корней алгебраического многочлена следующими численными методами: метод бисекции, метод хорд и касательных, метод разложения на множители с учетом определяемой точности.
-
Приближенное вычисление корней в уравнения
Приближённое решение уравнений: метод хорд, метод касательных, комбинированный способ.
-
Приближенное решение уравнений методом хорд и касательных
Магнитогорский государственный технический университет Приближенное решение уравнений методом хорд и касательных Подготовил: Григоренко М.В. Студент группы ФГК-98
-
Решение нелинейных уравнений методом простых итераций
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ВОСТОЧНО-СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ Реферат на тему: «Решение нелинейных уравнений
-
Решение нелинейных уравнений
Графическое решение нелинейного уравнения. Уточнение значение одного из действительных решений уравнения методами половинного деления, Ньютона–Рафсона, секущих, простой итерации, хорд и касательных, конечно-разностным и комбинированным методом Ньютона.