Название: Розкриття невизначеностей за правилом Лопіталя

Вид работы: реферат

Рубрика: Математика

Размер файла: 148.06 Kb

Скачать файл: referat.me-216072.docx

Краткое описание работы: Міністерство охорони здоров’я України Житомирський фармацевтичний коледж ім. Г.С. Протасевича Реферат на тему: “ Розкриття невизначеностей за правилом Лопіталя”

Розкриття невизначеностей за правилом Лопіталя

Міністерство охорони здоров’я України

Житомирський фармацевтичний коледж

ім. Г.С. Протасевича

Реферат

на тему:

“ Розкриття невизначеностей за правилом Лопіталя ”

Роботу виконала

Студентка 211 групи

Піщук Олеся

Викладач:

Виговська В.Г.

Отриманий бал:

_____________

м. Житомир – 2006

План

І. Розкриття невизначеностей з використанням правила Лопіталя.

1) Правило Лопіталя.

а) Наслідок.

б) Приклад 1.

2) Розкриття невизначеностей виду: ∞-∞; 0∙∞; 1^∞ ; 0⁰ ; ∞⁰ .

а) Приклад 2.

б) Приклад 3.

в) Приклад 4.

Список використаної літератури.

І. Розкриття невизначеностей з використанням правила Лопіталя.

Лопіталь де Гійом Франсуа (1661-2.02.1704 рр.). Французький математик, член Парижської АН, народився в Парижі, вивчав математику під керівництвом У. Бернуллі. Видав перший друкований підручник по диференціальному обчисленню – “Аналіз нескінченно малих” (1696р.). В підручнику є правило Лопіталя – правило знаходження межі дробу, чисельник і знаменник якого прямує до 0. Крім того, він створив курс аналітичної геометрії конічних перетинів. Йому також належить дослідження і розвиток за допомогою математичного аналізу декількох важких задач по геометрії і механіці, а також одне із рівнянь знаменитої задачі о браністохроні.

1. Правило Лопіталя.

Нехай виконані умови:

1. функції f(х) та g(х) визначені і диференційовані в колі точки х₀ ;

2. частка цих функцій в точці х₀ має невизначеність вигляду або ;

3. існує .

Тоді існує і виконує рівність:

(1)

а) Наслідок.

Нехай:

1. Визначені в колі точки х₀ функції f(х), g(х) та їх похідні до n -го порядку включно;

2. Частки , , …, мають невизначеність вигляду або ;

3. Існує , тоді

(2)

б) Приклад 1.

Знайти: .

Розв’язання:

Функції та визначені з усіма своїми похідними в околі точки х=0 .

Маємо:

.

2) Розкриття невизначеностей виду: ∞-∞; 0∙∞; 1^∞ ; 0⁰ ; ∞⁰ .

Існують прийоми, що дозволяють зводити вказані невизначеності до невизначеностей вигляду або , які можна розкривати з використанням правила Лопіталя.

1. Нехай і , тоді

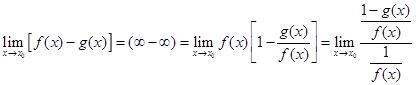(3)

За умовою при , тому при .

Якщо не прямує до 0 при , то границя в правій частині (3) не існує, а тому і границя лівої частини (3) не існує.

Якщо при , то вираз 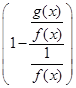має невизначеність .

2. Нехай , , тоді має невизначеність вигляду при .

В цьому випадку поступають так:

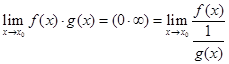
Під знаком останньої границі маємо невизначеність .

3. Нехай , при . Тоді має невизначеність вигляду .

Позначимо . Шляхом логарифмування цієї рівності одержимо:

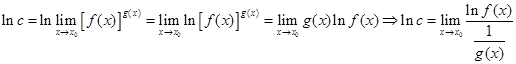
Отже, обчислення натурального логарифма границі зводиться до розкриття невизначеності вигляду .

4. Невизначеності вигляду та зводять до невизначеностей або шляхом логарифмування аналогічно до невизначеності вигляду .

а) Приклад 2.

Знайти границю .

Розв’язання:

Функції та диференційовані, а їх частка має невизначеність вигляду при .

Використовуючи правило Лопіталя, одержимо:

.

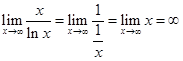б) Приклад 3.

Знайти границю .

Розв’язання:

В цьому випадку маємо невизначеність вигляду . Позначимо і про логарифмуємо цю рівність. Одержимо:

, тобто невизначеність вигляду . Використовуючи правило Лопіталя, одержимо:

.

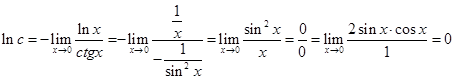Отже, .

в) Приклад 4.

Знайти границю .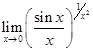

В цьому випадку маємо невизначеність вигляду . Нехай 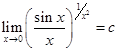. Логарифмуючи цю рівність, одержимо:

.

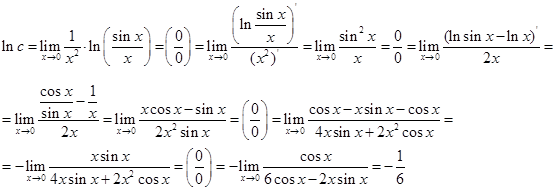Чотири рази застосували правило Лопіталя.

Отже, маємо:

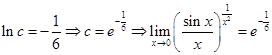
Список використаної літератури:

1. Кривуца В.Г., Барковський В.В., Барковська Н.В. К.82. Вища математика. Практикум. Навчальний посібник.–Київ: Центр навчальної літератури, 2005.–536с.

2. Бородин А.И., Бугай А.С., Биографический словарь деятелей в области математики. Радянська школа 1979.

3. Алгебра и начала анализа: В 2-х ч./ Под. ред. Г.Н. Яковлева.–2-е изд. –К.: Вища шк., Головное изд-во, 1984.–Ч.2. 293с.