Название: Задачи по Высшей математике

Вид работы: реферат

Рубрика: Математика

Размер файла: 24.25 Kb

Скачать файл: referat.me-216232.docx

Краткое описание работы: Вариант № 2 Задача 1 Найти объединение и пересечение множеств А и В, если А ={1;3;5} и B={0;1;2;-3;4;-5}. Решение: Объединение множеств А и В А  В= {0;1;2;3;5;-3;4;-5},

Задачи по Высшей математике

Вариант № 2

Задача 1

1. Найти объединение и пересечение множеств А и В, если А ={1;3;5} и B={0;1;2;-3;4;-5}.

Решение: Объединение множеств А и В

А È В= {0;1;2;3;5;-3;4;-5},

А ÇВ={1}.

Задача 2

2. Используя законы де Моргана, преобразовать следующую формулу та, чтобы знак отрицания был отнесен к отдельным переменным Ø( pqÚØq)

Решение:

Используя формулы де Моргана, раскроем скобки

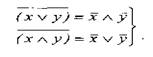ПолучимØ(pq ÚØq) Û Ø(pq) ÙØ(Øq) Û Ø(pq)Ùq Û ØpÙØqÙq

Задача 3

Пусть В — отношение «быть братом», С — отношение «быть сестрой». Описать отношения

а)В È С

б) В ∩ С

1) Объединение всех братьев и всех сестер

2) Пересечение, то есть люди, являющиеся одновременно и братом и сестрой.

В ∩ С.Отношения B и C определены над неким множеством M. Любые два элемента x и y этого множества либо находятся, либо не находятся в этих отношениях.

Отношение В ∩ С также определено над множеством M, причем элементы x и y находятся между собой в этом отношении тогда, и только тогда, когда:

1. xBy и xCy

2. xBy и yCx

Предположим, что M - это люди. Тогда отношение B•C описывает случай, когда x и y являются братом и сестрой (например, Саша является братом Маши, а Маша является сестрой Саши. Саша и Маша находятся в отношении B•C).

. Отношение В È С или B+C (обозначим его R)

- антирефлексивно (для любого элемента x из множества M пара (x, x) не находятся в отношении R (сам себе не являешься ни братом, ни сестрой))

- симметрично (для любых элементов x и y из M если xRy, то и yRx (я являюсь братом (или сестрой) своему брату или сестре)

- транзитивно (для любых элементов x, y и z из M если xRy и yRz, то xRz (брат или сестра моего брата или сестры является моим братом или сестрой)

2. Отношение В ∩ С (также обозначим R)

- антирефлексивно

- антисимметрично (для любых элементов x и y из M если xRy и yRx, то x=y; но т.к. любые два элемента не могут одновременно находиться в этих отношениях, то посылка является ложной, то есть все высказывание истинно)

- асимметрично (т.к. оно антирефлексивно и антисимметрично; для любых элементов x и y из M если xRy то (не yRx))

- транзитивно (для любых элементов x, y и z из M если xRy и yRz, то xRz; но у нас посылка всегда ложна (если xRy, то x - сестра, а y - брат; следовательно, y никак не может быть в отношении R ни с одним элементом z, т.к. для этого он должен быть сестрой z. Т.о., посылка ложна при любых x, y и z, а следовательно, все условие истинно))

Задача 4

найти интеграл

Задача 5

Вероятность попадания в мишень для первого стрелка равна 0.5, а для второго 0,8. Найти вероятность того. Что после первого залпа будет хотя бы один бы один промах.

Решение:

Обозначим событие А₁ попадание в цель первым стрелком, событие А₂ — попадание вторым стрелком. Промах первого обозначим Ᾱ₁ , промах второго Ᾱ₂ .

Р( А₁ )= 0,5; Р( Ᾱ₁ )= 1- 0,5=0,5; Р(А₂ )=0,8; Р(Ᾱ₂ )=1-0,8= 0,2.

Вероятность события В, что после первого залпа будет хотя бы один промах равна

Р(В)=Р( А₁ )∙Р(Ᾱ₂ )+Р( Ᾱ₁ )∙Р(А₂ )=0,5∙0,2+0,5∙0,8=0,5.

Ответ: вероятность того, что после первого залпа будет хотя бы один промах равна 0,5.