Referat.me
/ / Вычисление интеграла фукции f (x) (методом Симпсона WinWord)

Название: Вычисление интеграла фукции f (x) (методом Симпсона WinWord)

Вид работы: реферат

Рубрика: Математика

Размер файла: 124.61 Kb

Скачать файл: referat.me-216833.docx

Краткое описание работы: С О Д Е Р Ж А Н И Е Введение 2 Глава 2. Постановка задачи 3 Глава 3. Математическая часть 4 Глава 4. Описание метода решения задачи 9 Глава 5. Описание алгоритма решения задачи 10

Вычисление интеграла фукции f (x) (методом Симпсона WinWord)

С О Д Е Р Ж А Н И Е

Введение..................................................................................................... 2

1. Постановка задачи.......................................................................... 3

2. Математическая часть................................................................... 4

3. Описание метода решения задачи.......................................... 9

4. Описание алгоритма решения задачи................................. 10

5. Текст программы............................................................................. 11

6. Результаты работы программы................................................ 15

Заключение............................................................................................. 16

Список использованных источников:................................................... 17

Введение

История появления и развития персональных компьютеров является одним из наиболее впечатляющих явлений нашего века. С момента появления первых образцов персональных компьютеров прошло меньше 25 лет, но сейчас без них уже немыслимо огромное количество областей человеческой деятельности - экономика, управление, наука, инженерное дело, издательское дело, образование, культура и т.д. Интерес к персональным компьютерам постоянно растет, а круг их пользователей непрерывно расширяется. В число пользователей ПЭВМ вовлекаются как новички в компьютерном деле, так и специалисты по другим классам ЭВМ.

Язык Паскаль - это один из наиболее распространённых языков программирования 80-90х годов , поддерживающий самые современные методологии проектирования программ (нисходящее, модульное проектирование, структурное программирование) имеют свою достаточно богатую историю развития.

Новую жизнь языку дала фирма Борланд, разработавшая на его базе семейство Паскаль – систем, называемых Турбо Паскалем. Интегрированная среда, обеспечивающая многооконную разработку программной системы, обширный набор встроенный в неё средств компиляции и отладки , доступный для работы через легко осваиваемое меню, - всё это обеспечивает высокую производительность труда программиста, недостижимую при работе со старыми средами.

Язык Турбо Паскаль хорошо подходит для обучения программированию.

1. Постановка задачи

Заданием на курсовую работу является создание программы на языке программирования Турбо Паскаль, которая должна осуществлять решение следующей задачи :

Вычислить приближённое значение интеграла функции f(x) на интервале с точностью до 0.01 методами Симпсона и трапеции с целью сравнения.

Интегрируемая функция: .

Определить метод, который решает поставленную задачу за минимальное число повторений.

Построить график функции f(x) на заданном интервале. Решить поставленную задачу с использованием функций и процедур алгоритмического языка Турбо Паскаль.

2. Математическая часть

Для приближённого вычисления интеграла функции f(x) используются методы приближённого интегрирования, наиболее употребительные из них основаны на замене интеграла конечной суммой. Для вычисления промежуток от a(x0 ) до b(xn ) разбивается на n равных частей, и для точек деления x0 , x1 , x2 , x3 , . . . , xn-1 , xn вычисляются значения интегрируемой функции y. Затем необходимо воспользоваться формулой приближённого интегрирования:

1) Формула трапеций (рис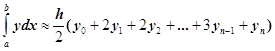.1) :

.(1)

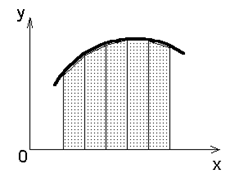
Рис.1.

2) Формула Cимпсона (парабол) (рис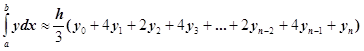.2) :

(2)

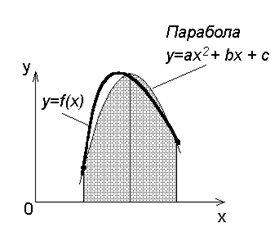
Рис.2.

В моей курсовой работе рассматривается приближенное вычисление интеграла 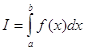(1)

При его аппроксимации заменим функцию f(x) параболой, проходящей через точки т.е представим приближенно f(x) в виде

где - интерполяционный многочлен Лагранжа второй степени,

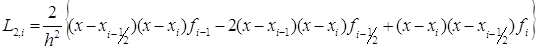. (2)

Проводя интегрирование получим

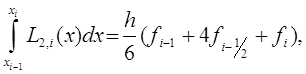
Таким образом приходим к приближенному равенству

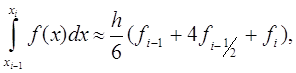(3)

Котрое называется формулой Симпсона или формулой парабол.

На всем отрезке [a,b] формула Симпсона имеет вид

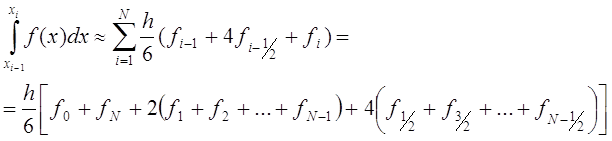
Чтобы не использовать дробных индексов можно обозначить

xi =a+0,5hi, fi =f(xi ), i=1,2,…,2N, hN=b-a

и записать формулу Симпсона в виде

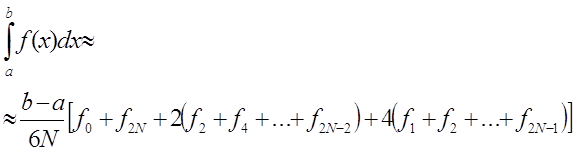(4)

Прежде чем переходить к оценке погрешности формулы (3) заметим, что она является точной для любого многочлена третьей степени, т.е. имеет место точное равенство

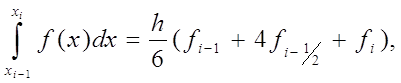
если f(x)=a0 +a1 x+a2 x2 +a3 x3 . Это утверждение нетрудно проверить непосредственно.

Для оценки погрешности формулы Симпсона воспользуемся интерполяционным многочленом Эрмита. Построим многочлен третьей степени H3 (x) такой, что

.

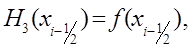
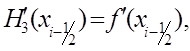
Такой многочлен существует и единствен.

Однако нам даже не потребуется явный вид многочлена H3 (x). Вспоминая, что формула Симпсона точна для любого многочлена третьей степени, получим

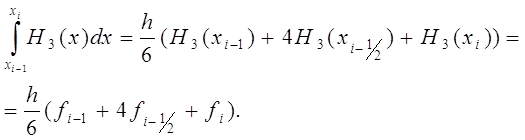(5)

Представим теперь f(x) в виде

f(x)=H3 (x)+ri (x), xÎ[xi-1 ,xi ], (6)

где ri (x) – погрешность интерполирования многочленом Эрмита H3 (x). Интегрируя (6) и учитывая (5), получим

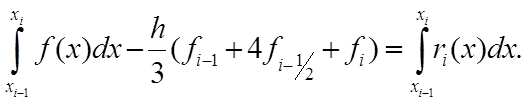(7)

Далее имеем

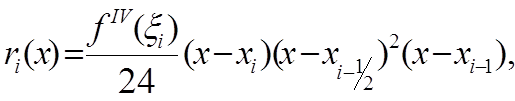
поэтому из (7) для погрешности формулы (3) получаем оценку

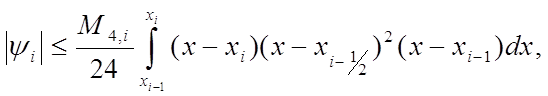
где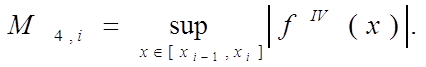

Вычисляя интеграл приходим к окончательной оценке

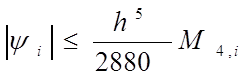(8)

Погрешность составной формулы Симпсона оценивается так

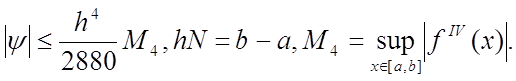(9)

Отсюда видно, что формула Симпсона существенно точнее, чем формулы прямоугольников и трапеций. На частичном отрезке она имеет точность О(h5 ), а на всем отрезке – O(h4 )

3. Описание метода решения задачи

Для решения поставленной задачи необходимо выполнить следующие действия:

1) Ввести значения границ отрезков;

2) Вывести график функции на экран с учётом масштаба;

3) Вычислить интеграл методом трапеций;

4) Вычислить интеграл методом Симпсона;

Для успешной реализации этих действий программа должна состоять из следующих функциональных модулей:

1) Функция f - вычисляет значение интегрируемой функции;

2) Функция trap - вычисляет интеграл методом трапеций;

3) Функция simpson - вычисляет интеграл методом Симпсона;

4) Процедура norm - вычисляет порядок числа, необходимый для построения графика функции с учётом масштаба;

5) Процедура out_gr - строит график функции на экране а графическом режиме с учётом масштаба.

Основная (главная) программа должна осуществлять ввод значения границ отрезков, вызов функций и процедур вычисления и вывод результатов на экран.

4. Описание алгоритма решения задачи

В соответствии с приведённым словесным описанием алгоритма решения поставленной задачи разработана блок схема решаемой задачи, которая изображена на рис. 3.

В изображенном алгоритме блоки имеют описанное ниже назначение:

Блок 1. Начало программы;

Блок 2. Очистка экрана;;

Блок 3. Запрос на ввод значений А и В;

Блок 4. Ввод значений А и В с клавиатуры;

Блок 5. Вызов процедуры вывода графика функции на экран;

Блок 6. Установка начального значения счётчика отрезков равным 3;

Блок 7. Вычисление значения начального значения интеграла методом трапеций;

Блок 8. Запоминание предыдущего значения интеграла, вычисленного методом трапеций, увеличение значения числа отрезков на 2, вычисление следующего значения интеграла методом трапеций;

Блок 9. Проверка условия : абсолютное значение разности текущего и предыдущего значений интегрирования меньше чем 0.001, если да, то выход из цикла, если нет, то переход на блок 8.

Блок 10. Вывод результатов, полученных при вычислении интеграла методом трапеций на экран.

Блок 11. Установка начального значения счётчика отрезков равным 3;

Блок 12. Вычисление значения начального значения интеграла методом Симпсона;

Блок 13. Запоминание предыдущего значения интеграла, вычисленного методом Симпсона, увеличение значения числа отрезков на 2, вычисление следующего значения интеграла методом Симпсона;

Блок 14. Проверка условия: абсолютное значение разности текущего и предыдущего значений интегрирования меньше чем 0.001, если да, то выход из цикла, если нет, то переход на блок 13.

Блок 15. Вывод результатов, полученных при вычислении интеграла методом Симпсона на экран.

Блок 16. Конец программы.

5. Текст программы

program tr_s;

uses crt,graph;

var

a,b:real; { Границы отрезка }

r,r2:real; { Предыдущее и текущее приближенные значения интеграла}

n:integer; { Счетчик }

{ Интегрируемая функция }

function f(x:real):real;

begin

f:=1/(x*ln(x)*0.43429);

end;

{ Метод трапеций }

function trap(a,b:real;n:integer):real;

var

s:real; { Полученная сумма }

h:real; { Шаг }

m:integer; { Счетчик }

begin

h:=(b-a)/(n-1); { Определяется шаг }

s:=(f(a)+f(b))/2; { Начальное значение суммы }

for m:=1 to n-2 do s:=s+f(a+m*h); { Суммиование остальных элементов}

trap:=s*h; { Возвращается значение интеграла }

end;

{ Метод Симпсона }

function simpson(a,b:real;n:integer):real;

var

s:real; { Сумма }

h:real; { Шаг }

m:integer; { Счетчик }

mn:integer; { Очередной множитель }

begin

h:=(b-a)/(n-1); { Рассчитывается шаг }

s:=f(a)+f(b); { Начальное значение шага }

mn:=4; { Первый мнодитель - 4 }

{ Суммирование остальных элементов }

for m:=1 to n-2 do begin

s:=s+mn*f(a+h*m);

if (mn=4) then mn:=2 else mn:=4;{ Именение мноителя 2<>4 }

end;

simpson:=s*h/3; { Возвращается вычисленное значение }

end;

{ Процедура вычисления порядка числа }

procedure norm(a:real);

var n:real;

begin

{ Если число слишком мало - возвращается ноль }

if (a<0.00001) then n:=0

else begin

{ Если число меньше единицы }

if (a<1) then begin

n:=1;

repeat

a:=a*10;

n:=n/10;

until (trunc(a)<>0);

end else begin

{ Если число больше единицы }

n:=1;

repeat

a:=a/10;

n:=n*10;

until (trunc(a)=0);

end;

end;

a:=n;

end;

{ Построение графика функции }

procedure out_grp(xmin,xmax,ymin,ymax:real);

var

drv,mode:integer;

mx,my:real; { Масштабы по осям }

xx,yy:real; { Текущие координаты }

sx:real; { Шаг по оси X }

dltx,dlty:integer;{ Приращение на графике при смещении графика }

s:string; { Строка }

begin

{ Инициализация графики }

drv:=VGA;

mode:=VGAHi;

initgraph(drv,mode,'');

{ Выяснение порядков минимумов и максимумов }

norm(xmax);

norm(ymax);

norm(ymin);ymin:=ymin/10;

norm(xmin);ymin:=ymin/10;

if (xmin/xmax)>0.01 then dltx:=20 else dltx:=0;

if (ymin/ymax)>0.01 then dlty:=20 else dlty:=0;

{ Расчет масштабов }

mx:=500/(xmax-xmin);

my:=400/(ymax-ymin);

{ Расчет приращения по X }

sx:=(xmax-xmin)/550;

{ Вывод системы координат }

settextjustify(1,1);

xx:=xmin;

repeat

setcolor(1);

line(trunc(40+mx*(xx-xmin)+dltx),20,trunc(40+mx*(xx-xmin)+dltx),469);

str(xx:4:2,s);

setcolor(15);

outtextxy(trunc(40+mx*(xx-xmin)+dltx),475,s);

xx:=xx+50*sx;

until (xx>(xmax+50*sx));

yy:=ymin+(ymax-ymin)/10;

repeat

setcolor(1);

line(41,trunc(470-my*(yy-ymin)-dlty),630,trunc(470-my*(yy-ymin)-dlty));

str(yy:4:2,s);

setcolor(15);

outtextxy(20,trunc(470-my*(yy-ymin)-dlty),s);

yy:=yy+(ymax-ymin)/10;

until (yy>(ymax+(ymax-ymin)/10));

line(40,0,40,480);

line(0,470,640,470);

line(40,0,38,10);

line(40,0,42,10);

line(640,470,630,472);

line(640,470,630,468);

{ Вывод графика }

xx:=xmin;

repeat

yy:=f(xx);

putpixel(trunc(40+mx*(xx-xmin)+dltx),trunc(470-my*(yy-ymin)-dlty),7);

xx:=xx+sx;

until (xx>xmax);

outtextxy(300,10,' Press ESC to continue ');

repeat until (readkey=#27);

closegraph;

end;

{ Основная программа }

begin

{ Ввод границ отрезков }

clrscr;

write(' Введите A,B: ');

readln(a,b);

{ Выводится график функции }

out_grp(a,b,f(b),f(a));

{ Вычисляется интеграл по методу трапеций }

n:=3;

r:=trap(a,b,n); { Начальное значение }

repeat

r2:=r; { Запоминается предыдущее значение }

n:=n+2; { Увеличивается количество шагов }

r:=trap(a,b,n); { Рассчитывается новое значение }

until (abs(r-r2)<0.001);{ Повторяется до достижения необходимой точности }

{ Вывод результатов }

writeln(' Резльтат по методу трапеций равен: ',r:6:3);

writeln(' для получения необходимой точности

интервал был разбит на');

writeln(n,' отрезков');

{ Вычисляется интеграл по методу Симпсона }

n:=3;

r:=simpson(a,b,n); { Начальное значение }

repeat

r2:=r; { Запоминается предыдущее значение }

n:=n+2; { Увеличивается количество шагов }

r:=simpson(a,b,n); { Рассчитывается новое значение }

until (abs(r-r2)<0.001);{ Повторяется до достижения необходимой

точности }

{ Вывод результатов }

writeln;

writeln(' Резльтат по методу Симпсона равен: ',r:6:3);

writeln(' для получения необходимой точности интервал

был разбит на ');

writeln(n,' отрезков');

end.

6. Результаты работы программы

Введите A,B: 2 3

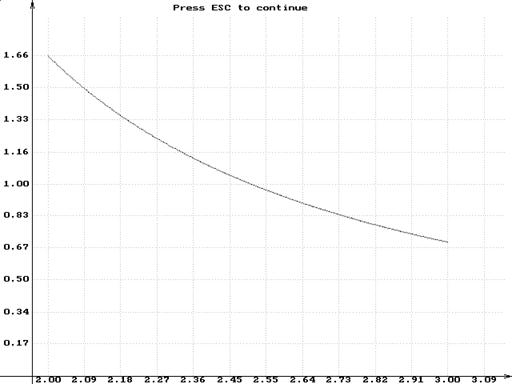
Результат по методу трапеций равен: 1.062

для получения необходимой точности интервал был разбит на 11 отрезков

Результат по методу Симпсона равен: 1.061

для получения необходимой точности интервал был разбит на 7 отрезков.

Анализ полученных в ходе работы программы результатов говорит о том, что поставленная задача успешно решается.

Метод трапеции является наиболее простым методом приближённого интегрирования , этот метод позволяет точно интегрировать многочлен первой степени , а для интегрирования данной функции требуется довольно много итераций. Более совершенным является метод Симпсона , который позволяет точно интегрировать многочлен второй производной и даже некоторые многочлены третьей степени, поэтому он требует почти в 2 раза меньше количества интервалов для получения результата.

Заключение

В данной курсовой работе решена задача приближённого интегрирования функции

методами Симпсона и трапеции.

В процессе создания курсовой работы разработан алгоритм решения поставленной задачи. По этому алгоритму на языке Турбо Паскаль 7.0. составлена и отлажена программа.

В ходе тестирования были получены результаты работы метода трапеции и метода Симпсона, по которым видно, что результаты интегрирования обоими методами совпадают с достаточной точностью. Заметна лишь разница в качестве приближения интервалов.

Программа является полностью работоспособной, что подтверждается результатами её тестированием..

Список использованных источников:

1.Бронштейн И.Н., Семендяев К.А. Справочник по высшей математике для инженеров и учащихся втузов. - М.: Наука , 1981 . - 718 с.

2.Белецкий Я. Турбо Паскаль с графикой для персональных компьютеров перевод с польского Д.И.Юренкова. -М.: Машиностроение , 1991. - 320 с.

3.Сергиевский М.В., Шалашов А.В. Турбо Паскаль 7.0; язык, среда программирования. -М: Машиностроение.-1994,-254 с.ил.

4.Справочник по процедурам и функциям Borland Pascal 7.0. - Киев: Диалектика, 1993. - 272 с.

5.Самарский А.А, Гулин А.В. Численные методы.М.:Наука,1989. – 430 с.

Похожие работы