Referat.me
/ / Интеграл Пуассона

Название: Интеграл Пуассона

Вид работы: реферат

Рубрика: Математика

Размер файла: 59.78 Kb

Скачать файл: referat.me-216873.docx

Краткое описание работы: Пусть    –суммируемые на     - периодические, комплекснозначные функции. Через

Интеграл Пуассона

.

Пусть ¦(x ) , g (x ),x ÎR1 –суммируемые на [-p, p] , 2p- периодические, комплекснозначные функции. Через f * g(x) будем обозначать свертку

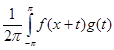f * g(x) =dt

Из теоремы Фубини легко следует, что свертка суммируемых функций также суммируема на [-p,p]и

cn ( f*g ) = cn ( f )× cn ( g ) , n = 0, ±1 , ±2 , ... ( 1 )

где {cn ( f )} -- коэффициенты Фурье функции f ( x ) :

cn = 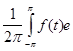-i n t dt , n = 0, ±1,±2,¼

Пусть ¦ÎL1 (-p,p) . Рассмотрим при 0£r <1 функцию

¦r ( x ) = n ( f ) r| n | ei n x , x Î[-p,p] , ( 2 )

где ряд в правой части равенства (2) сходится равномерно по х для любого фиксированного r , 0£r <1 . Коэффициенты Фурье функции ¦r (х)равны

cn ( fr ) = cn × r| n | , n = 0 , ±1,±2,¼, а это согласно (1) значит, что ¦r ( x ) можно представить в виде свертки :

¦r ( x ) = 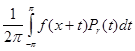, ( 3 )

где

, t Î[-p,p]. ( 4 )

Функция двух переменных Рr (t) , 0 £r<1 , t Î[-p,p] , называется ядром Пуассона , а интеграл (3) -- интегралом Пуассона .

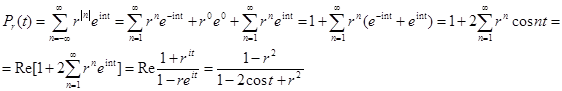
Следовательно,

Pr ( t ) = , 0£r <1, t Î[-p,p] . ( 5 )

Если ¦Î L1 ( -p,p ) -действительная функция , то , учитывая , что

c-n ( f ) = `cn ( f ) , n = 0,±1,±2,¼,из соотношения (2) мы получим :

fr ( x ) =

=, ( 6 )

где

F ( z ) = c0 ( f ) + 2 ( z = reix ) ( 7 )

- аналитическая в единичном круге функция . Равенство (6) показывает, что для любой действительной функции ¦ÎL1 ( -p, p ) интегралом Пуассона (3) определяется гармоническая в единичном круге функция

u ( z ) = ¦r (eix ) , z = reix , 0 £ r <1 , x Î [ -p, p ] .

При этом гармонически сопряженная с u (z) функция v (z) c v (0) = 0 задается формулой

v (z) = Im F (z) = . ( 8 )

Утверждение1.

Пусть u (z) - гармоническая ( или аналитическая ) в круге |z |<1+e(e>0)функция и ¦ (x) = u (eix ) , xÎ[-p, p] . Тогда

u (z) = 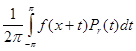( z = reix , | z |<1 ) ( 10 ).

Так как ядро Пуассона Pr (t) - действительная функция, то равенство (10) достаточно проверить в случае, когда u (z) - аналитическая функция:

=, | z |<1+ e .

Но тогда

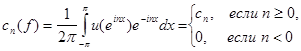
и равенство (10) сразу следует из (2) и (3).

Прежде чем перейти к изучению поведения функции ¦r (x ) при r®1 , отметим некоторые свойства ядра Пуассона:

а) ;

б) ;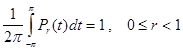

в) для любого d>0

Соотношения а) и в) сразу следуют из формулы (5), а для доказательства б) достаточно положить в (2) и (3) ¦(х)º1.

Теорема 1.

Для произвольной (комплекснозначной) функции ( -p, p ) , 1 £ p < ¥ , имеет место равенство

;

если же ¦ (x) непрерывна на [ -p, p ] и ¦ (-p) = ¦ (p) , то

.

Доказательство.

В силу (3) и свойства б) ядра Пуассона

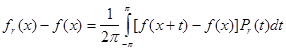( 12 )

Для любой функции , пользуясь неравенством Гельдера и положительностью ядра Пуассона , находим

.

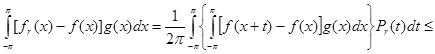
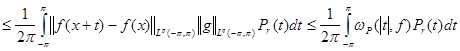Следовательно,

.

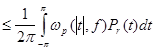Для данного e>0 найдем d = d (e) такое, что . Тогда для r , достаточно близких к единице, мы получим оценку

.

Аналогично второе неравенство вытекает из неравенства

.

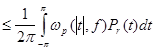Теорема 1 доказана.

Дадим определения понятий "максимальная функция" и "оператор слабого типа", которые понадобятся нам в ходе доказательства следующей теоремы.

Определение1.

Пусть функция суммируема на любом интервале (-А, А), А > 0 . Максимальной функцией для функции называется функция

где супремум берется по всем интервалам I , содержащим точку х.

Определение 2.

Оператор называется оператором слабого типа (р,р) , если для любого y > 0

.

Теорема 2 (Фату).

Пусть - комплекснозначная функция из . Тогда

для п.в. .

Доказательство.

Покажем, что для и

, ( 13 )

где С - абсолютная константа , а M ( f, x ) - максимальная функция для f (x) [*] . Для этой цели используем легко выводимую из (5) оценку

(К - абсолютная константа).

Пусть - такое число, что

.

Тогда для

.

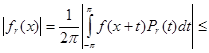
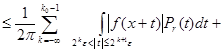
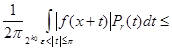
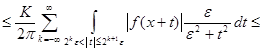
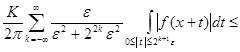
Неравенство (13) доказано. Используя затем слабый тип (1,1) оператора , найдем такую последовательность функций ,что

,

( 14 )

для п.в. .

Согласно (13) при xÎ (-2p,2p)

Учитывая , что по теореме 1 для каждого xÎ [-p,p] и (14)

Из последней оценки получим

при n®¥.

Теорема 2 доказана.

Замечание.

Используя вместо (13) более сильное неравенство (59), которое мы докажем позже, можно показать, что для п.в. xÎ [-p,p] , когда точка reit стремится к eix по некасательному к окружности пути.


[*] Мы считаем , что f (x) продолжена с сохранением периодичности на отрезок [-2p,2p] (т.е.
f (x) = f (y) , если x,y Î [-2p,2p] иx-y=2 p ) и f (x) = 0 , если |x |>2p.

Похожие работы